Driehoeksconstructies

Overzicht ][ Meetkunde | Trisectie (penl-constructies) | Cabri

Overzicht

Inleiding - basisconstructies
Constructies met andere dan de basiselementen / Overzicht
2.1. Eenvoudige constructies
2.2. Complexe(re) constructies
Constructies met om- en incirkel
Bijzondere constructies

[Deze pagina is in bewerking]

1. Inleiding - basisconstructies
Het is bekend dat een driehoek in de volgende gevallen met passer en liniaal construeerbaar is:

1.	ZZZ	: de drie zijden zijn gegeven; deze worden in hetgeen volgt aangegeven met a, b, c
2.	ZHZ	: er zijn twee zijden gegeven en de door die zijden ingesloten hoek; bijvoorbeeld A, b, c
3.	HZH	: er zijn twee hoeken gegeven en gemeenschappelijke zijde van die hoeken; bijvoorbeeld A, B, c
4.	ZHH	: er zijn twee hoeken geven en een zijde tegenover één van die hoeken; bijvoorbeeld A, B, a
5.	ZZR	: er zijn twee zijden gegeven en de rechte hoek tegenover de grootste van die zijden

Bovenstaande constructies zijn gebaseerd op de zogenoemde congruentiegevallen of congruentiekernmerken die ook met bovenstaande drie letters worden aangeduid. We zouden ze hier constructiekenmerken kunnen noemen.

Opmerking
Geval 5 kan zwak worden geformlueerd als:

5b.

ZZH*

: er zijn twee zijden gegeven en de hoek tegenover één van die zijden

In dit geval zijn er soms twee oplossingen, een oplossing met een scherpe en een oplossing met een stompe hoek.
[einde Opmerking]

We gaan er op deze pagina van uit, dat de constructies in de hierboven genoemde gevallen bekend zijn. En voorts ook constructies van bissectrices, hoogtelijnen, ed.
Bij een aantal constructies worden transformaties als vermenigvuldiging, (punt)spiegeling, rotaties, ed. gebruikt. Ook met die constructies wordt bekendheid ondersteld.

2. Constructies met andere dan de basiselementen
In de volgende paragrafen beschrijven we enkele constructies voor driehoeken waarvan ook andere dan drie basiselementen (hoeken, zijden) gegeven zijn, zoals hoogtelijnen, zwaartelijnen en bissectrices.
We zullen daarbij voor die andere elementen de volgende notaties gebruiken:

h_a, h_b, h_c	- hoogtelijnen op de zijden a, b, c (uit A, B, C)
z_a, z_b, z_c	- zwaartelijnen naar de zijden a, b, c (uit A, B, C)
d_a, d_b, d_c	- bissectrices van A, B, C
R, r	- opvolgend de straal van de omcirkel en de incirkel (zie daarvoor paragraaf 3)
r_a, r_b, r_c	- de stralen van de aancirkels aan de (dragers van de) zijden a, b, c (zie eveneens paragraaf 3)

Overzicht

geen zijde

met d, h, z

met R of r

bijzonder

[ a b ha ]

[ a ha hb ]

[ A a b + c ]

[ A ha a+b+c ]

[ da ha za ]

[ a b R ]

[ A X Xa ]

[ a b za ]

[ a ha za ]

[ A a b - c ]

[ A hb hc ]

[ a hb r ]

[ a b zc ]

[ a hb hc ]

[ A a ha ]

[ ha hb hc ]

[ A a r ]

[ O ha da ]

[ a b A - B ]

[ a hb zb ]

[ A a hb + hc ]

[ A zb b : c ]

[ ha hb za ]

[ A a hb - hc ]

[ A zb zc ]

[ A a - b r ]

[ a b-c hc ]

[ a zb zc ]

[ A a+b a+c ]

[ za zb zc ]

[ A b + c r ]

[ A b a + c ]

[ A - B ha hb ]

[ a B db ]

[ A b a - c ]

[ a - b ha r ]

[ a B b-ha ]

[ A B dc ]

[ a+b A-B ra+rb ]

[ a B ha ]

[ A B zc ]

[ ha hb r ]

[ a B - C ha ]

[ A B a+b+c ]

[ za r ra ]

2.1. Eenvoudige constructies
Deze constructies worden aangeduid met 'eenvoudig' omdat de constructie (min of meer direct) gebaseerd is op bovenstaande constructiekenmerken en/of op eenvoudige meetkundige plaatsen..

a, b, h_a

De punten B en C kiezen we in ligging gegeven, vastgelegd door a.
Het punt A ligt nu op de lijn(en) evenwijdig met BC en op afstand h_a (in de figuur is dat A'B) van BC - noem deze lijn (verzameling, meetkundige plaats) mp₁(A).
Het punt A ligt eveneens op de cirkel (C, b) - noem deze meetkundige plaats mp₂(A).
A is dan een snijpunt van mp₁(A) en mp₂(A).
We vinden dus ten hoogste twee (vier) punten A, dus ook ten hoogste twee (vier) driehoeken.

a, b, z_a
	De punten B en C kiezen we in ligging gegeven, vastgelegd door a. Het punt A ligt nu op de cirkel (M_a, z_a = z), waarbij M_a het midden is van BC. En A ligt ook op de cirkel (C, b). A is dus het snijpunt van beide cirkels.

a, b, z_c

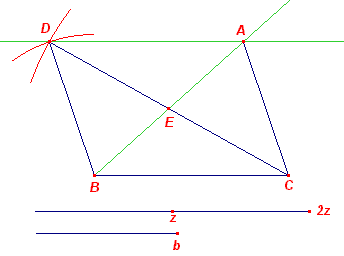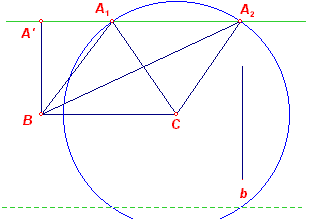
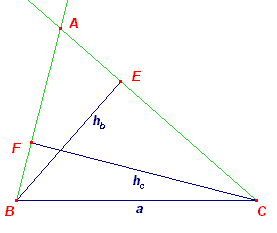
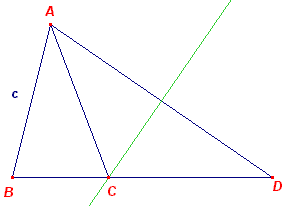
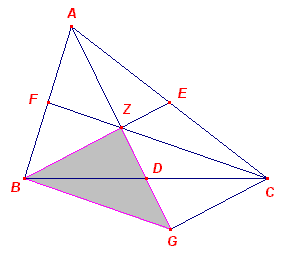
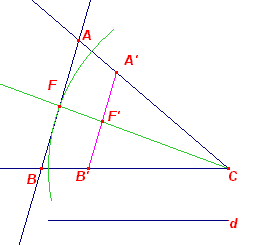
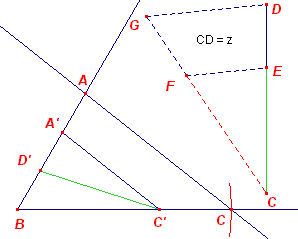
Eerste oplossing
De punten B en C kiezen we in ligging gegeven, vastgelegd door a.
We kunnen nu driehoek BCD construeren (ZZZ), waarbij CD = 2z en BD = b.
BCAD is dan een parallellogram.
A kan dus gevonden worden als snijpunt van de lijn BE (waarbij E het midden is van CD) en de lijn door D // BC.

Tweede oplossing
Klik hier voor een oplossing van het probleem met gebruikmaking van vermenigvuldiging (en meetkundige plaatsen).

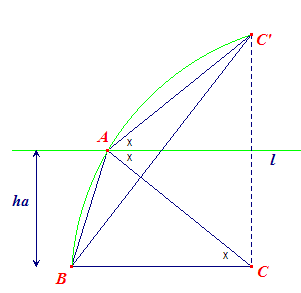
a, b, A - B / a, B - C, h_a
	Klik hier voor de constructiebeschrijving van beide gevallen. Opmerking [a, b, A - B] wordt geconstrueerd als [b, c, B - C]. Daarmee wordt [a, B - C, ha] daarmee in overeenstemming gebracht.

a, B, d_b
	De punten B en C kiezen we in ligging gegeven, vastgelegd door a. De halve hoek B is nu bekend, zodat BCD geconstrueerd kan worden (ZHZ). D is hier het snijpunt van de bissectrice uit B met de overstaande zijde (b). A wordt dan gevonden als snijpunt van de lijn CD met de zijde c.

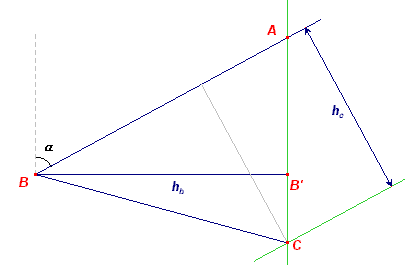
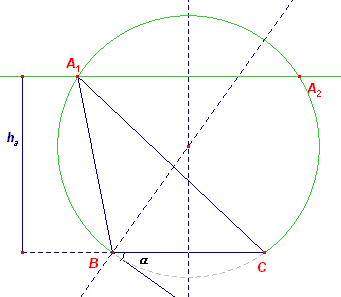
a, B, h_a
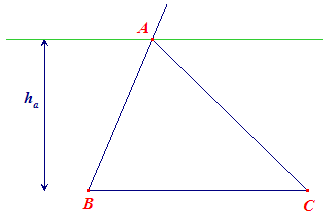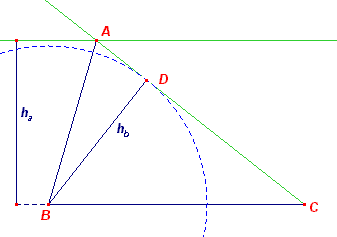
	Het punt A ligt op een afstand h_a van BC, dus op een lijn evenwijdig met BC en op afstand h_a van BC. Het punt A ligt eveneens op het niet met BC samenvallende been van hoek B.

.
a, h_a, h_b
	Eerste oplossing De driehoek BCD is direct construeerbaar (ZZR). De halve lijn CD snijdt de lijn evenwijdig met BC en op afstand h_a van BC in het punt A. Tweede oplossing Het punt A ligt ook op een raaklijn uit C aan de cirkel (B, h_b).
.
a, h_b, h_c
	De driehoeken BCE en BCF zijn direct construeerbaar (elk volgens ZZR). A is het snijpunt van de halve lijnen BF en CE.
.
a, h_b, z_b
	Driehoek BCD kan direct worden geconstrueerd (ZZR). De drager van CA (een halve lijn door C en D) snijdt de cirkel (B, z) in de punten B'₁ en B'₂. Met deze punten als centrum kunnen de punten A₁ en A₂ geconstrueerd met een puntspiegeling. Opmerking Als de cirkel de lijn CD niet, snijdt zijn er geen oplossingen. Als de cirkel de lijn CD raakt (in D), is er slechts één oplossing. Driehoek ABC is dan gelijkbenig.
.

a, h_a, z_a
	Het punt A ligt op afstand h_a van BC, dus op een lijn evenwijdig met BC en op afstand h_a van BC. Het punt A ligt ook op de cirkel met middelpunt D en straal z_a. Hierbij is D het midden van BC.

..
a, z_b, z_c
	De punten B en C zijn in ligging gegeven, vastgelegd door a. Nu is BCZ construeerbaar (ZZZ). E en F zijn de puntsymmetriebeelden van de middens van BZ en CZ in Z. De lijnen BF en CE snijden elkaar in A.
.

A, b, a+c >> B, c, a + b
	We kiezen B in ligging gegeven en bepalen D, met BD = a + b. Maar ook is de ligging van A bekend, immers c is gegeven. Driehoek ABD is dus construeerdbaar (ZHZ). Voor het punt C geldt nu CB = a, en dus CD = b, maar ook CA = b. C ligt dus op de middelloodlijn van DA, waarmee C als snijpunt van die middelloodlijn met BC gevonden kan worden.

A, b, a - c >> B, c, a - b
	Merk op, dat in dit geval a > b. We kiezen B in ligging gegeven en bepalen D met BD = a - b. Maar ook is de ligging van A bekend, immers B en c zijn gegeven. Driehoek ABD is dus construeerbaar (ZHZ). Op BD moet nu het punt C gevonden worden met CD = CA = b. C ligt dus op de middelloodlijn van AD, waarmee C gevonden kan worden als snijpunt van die middelloodlijn met BD.

A, B, a + b+ c >> B, C, a + b + c

In nevenstaande figuur is DE = a + b + c. Nu is:
in DBA: D = ½B
in CEA: E = ½C
We plaatsen de gegeven hoeken B en C dus met hoekpunten in D en E en een been langs DE.
Driehoek ADE is dan construeerbaar (HZH).
B ligt op de middelloodlijn van AD (immers BA = BD) en C ligt op de middelloodlijn van AE (immers CA = CE).
Maar ook B en C liggen op DE. Waarmee ABC eveneens gecosntrueerd is.
Opmerking
In plaats van de middelloodlijnen kunnen we ook lijnen door A trekken evenwijdig aan opvolgend FD en FC.
[einde Opmerking]

A, h_b, h_c
	Driehoek ABB' is direct construeerbaar (ZHH); daarbij is gebruik gemaakt van de hoek B = 90° - A. Het punt C ligt op AB' en op de lijn // AB en op afstand h_c van AB. Hiermee is het punt C gevonden.

z_a, z_b, z_c
	Kies op BE het punt Z zo, dat BZ = ²/₃BE. Ga er nu vanuit, dat driehoek ABC reeds geconstrueerd is. Zij G het puntsymmetrisch beeld van Z in D. Nu is BG = ZC = ²/₃CF, GZ = AZ = ²/₃AD. Driehoek BGZ is dus construeerbaar (ZZZ). Het puntspiegelbeeld van B in D (het midden van ZG) geeft C, het puntspiegelbeeld van G in Z geeft A.

2.2. Complexe(re) constructies

a, b - c, h_c
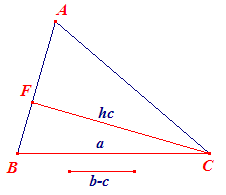	Klik hier voor de constructiebeschrijving.

a, A, b + c

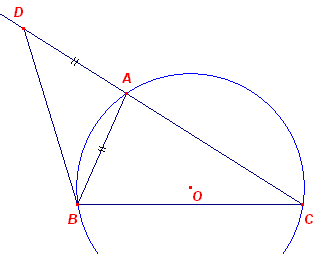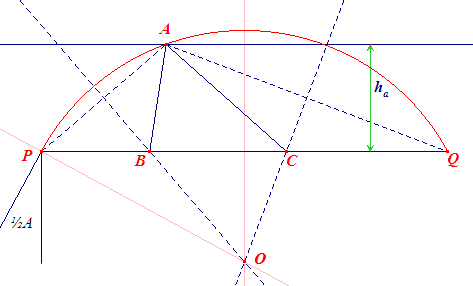
Zij driehoek ABC gegeven.
Is D het punt op het verlengde van CA, zodat CD = c + b.
Nu is in driehoek ABD:
D = ½(180 - (180 - A)) = ½A.

Driehoek BCD is dus construeerbaar (ZZH*).
De meetkundige plaats van het punt A is eveneens bekend (deel van de omcirkel van ABC; KoordeHoekBoog; stelling van de constante hoek).
A is dus constreerbaar als snijpunt van bg BC en CD.

Opmerking
Vanwege het constructiekenmerk ZZH* is ABC niet eenduidig bepaald.
[einde Opmerking]

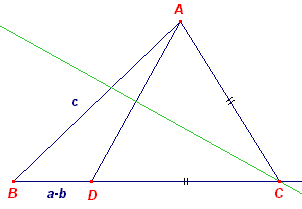
a, A, b - c

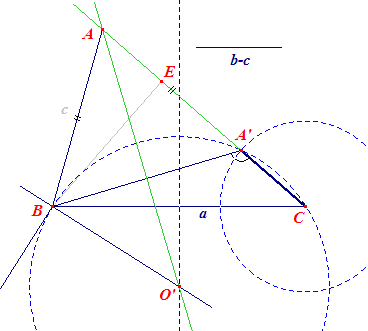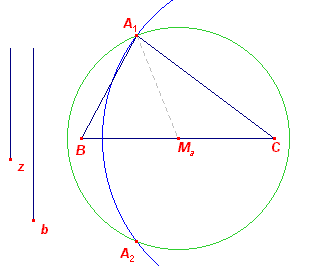
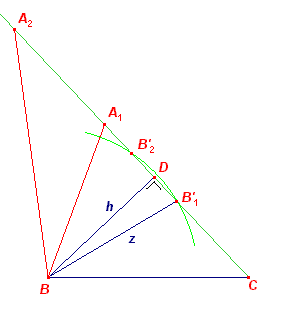
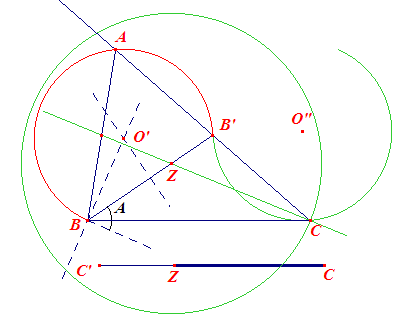
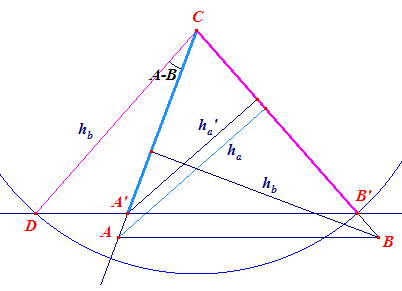
Het lijnstuk a is in ligging gegeven. Driehoek A'BC met CA' = b-c is construeerbaar.
Immers:
Uit AB = AA' = c volgt AA'DB = ABA' = ½(180 - A) = 90 - ½A.
Dus BA'C = 90 + ½A
A' ligt daardoor op de cirkel waaronder BC wordt gezien onder een hoek 90 + ½A. A' vinden we op deze cirkel (en wel op de kleinste boog) als snijpunt met de cirkel C(b-c).
A is dan het snijpunt van CA' met de middelloodlijn van A'B.

Opmerking
Het probleem is alleen oplosbaar als a > (b-c).
Omdat BA'C een stompe hoek is, vinden we slechts één oplossing.
Driehoek A'BC is ook construeerbaar volgens constructiekenmerk ZZH*.

N.b.
De hoogtelijn BE van driehoek ABC is tevens hoogtelijn van driehoek CA'B'.
Verder is CBA' = ABC - ABA' = B - (90 - ½A) = B + ½A + ½C - ½C - 90
zodat CBA' = ½(A+B+C) + ½(B-C) - 90 = ½(B-C).

a, A, h_b + h_c / a, A, h_b - h_c
	Klik hier voor de constructiebeschrijvingen.

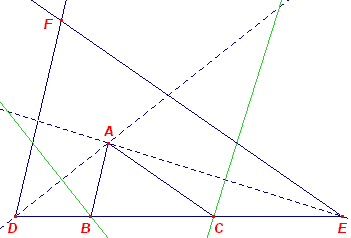
A, a + b, a + c

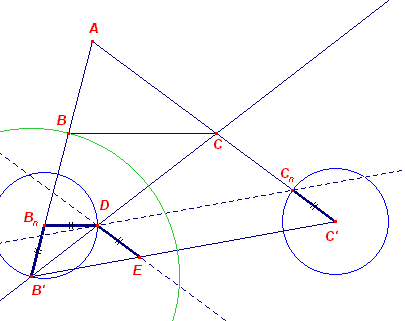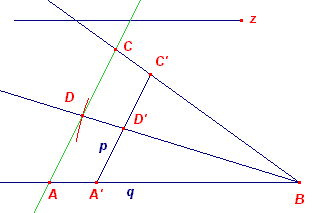
Eerste oplossing
Op basis van de gegevens is de driehoek AB'C' direct construeerbaar (ZHZ).
We moeten nu op B'A en C'A opvolgend de punten B en C construeren met B"B = BC = CC'.
We doen dit op basis van vermenigvuldiging van een kleinere figuur B'BnDE, die wordt geconstrueerd via de punten B_n en C_n op de zijden, met B'B_n = C'C_n (zie de beide cirkels).
Het punt D wordt dan gevonden als snijpunt van de lijn door Cn // B'C' met de cirkel rond Bn (die door B' gaat).
De lijn B'D snijdt dan de lijn AC' in het gezochte punt C.
Hiermee is de lengte van a = CC' gevonden.
B contrueren we op AB' met de cirkel (B', a).

Tweede oplossing
Klik hier voor een oplossing met behulp van projectieve eigenschappen

A, h_a, a + b + c

Stel het probleem is opgelost. Maak BP gelijk aan AB = c en CQ gelijk aan CA = b. Dan is PQ = 2s = a + b + c.
Dan is PAB = ½B en CAQ = ½C, zodat PAQ = 90° + ½A.
Het punt A ligt dus op een cirkelboog (stelling van de omtrekshoek). Maar A ligt ook op de lijn die de afstand ha tot PQ heeft.
Het punt A kunnen we dus vinden als snijpunten van die boog en die lijn.
B en C b\vinden we dan door de middelloodlijnen van BA em CA te snijden met de lijn PQ.

Constructie
De hoek A is gegeven als halve hoek in P.
O is het middelpunt van de boog die hoort bij (PQ, ½A).

A, z_b, b : c

We gaan ervan uit, dat de verhouding b : c vastgelegd wordt met behulp van twee lijnstukken p en q.
Met deze lijnstukken en hoek A kunnen we dan een driehoek A'BC' construeren die gelijkvormig is met ABC (ZHZ).
Daarna kunnen we een vermenigvuldiging toepassen met centrum B, waarbij het midden D' van A'C' overgaat in het midden D van AC. D kan via z = z_bworden bepaald op de lijn BD'; gebruik de cirkel (B, z).
De lijn door D evenwijdig aan A'C' geeft dan met de dragers van BA' en BC' opvolgend de punten A en C.

A, z_b, z_c

In driehoek ABB' is A en BB' (= z_b) gegeven. A ligt dus op een cirkelboog (omtrekshoek; middelpunt O').
C is het puntsymmetrisch beeldpunt van A tov. B'. C ligt dus eveneens op een cirkelboog, middelpunt O" (het puntspiegelbeeld van boog O' het punt B').
Het zwaartepunt Z op BB' is eveneens bekend. C ligt op een afstand van ²/₃CC' (= z_c) van Z. C ligt dus ook op een cirkel, te weten de cirkel (Z, ²/₃z_c). Hiermee is het punt C gevonden. De halve lijn CB' snijdt dan de eerste cirkelboog in A. En tenslotte tekenen we de zijde BA.

Opmerking
De hoek A is in nevenstaande tekening in ligging gegeven. Een been van hoek A valt samen met de (halve) lijn BB'. Hiermee wordt de constructie van boog O' vereenvoudigd.

A, B, d_c

Twee hoeken van een driehoek (in dit geval de gegeven hoeken A en B) bepalen een verzameling gelijkvormige driehoeken.
We kunnen de gevraagde driehoek dus vinden via een vermenigvuldiging met het punt C als centrum.
Zij A'B'C een van die driehoeken.
De bissectrice van hoek C snijdt A'B' in F'. De lijn door F' snijdt de cirkel (C, d) in het punt F.
De lijn door F evenwijdig met A'B' snijdt de halve lijnen CA' en CB' opvolgend in de gezochte punten A en B.

A, B, z_c

Uit het gegeven volgt ook hoek C.
We kunnen nu een driehoek BC'A' construeren die gelijkvormig is met driehoek BCA.
In driehoek BC'A' is C'D' zwaartelijn. We kunnen dan de factor bepalen, waarmee C'D' = z' moet worden vermenigvuldig om CD = z te krijgen.
Deze factor kunnen we gebruiken bij een vermenigvuldiging van A'C' met centrum B.
Die vermenigvuldiging geeft dan A en C.
We hebben in de hulpconstructie in nevenstaande figuur:
CE = C'D', CD = z, CF = BC' = a', CG = BC = a.
Uit de hulpconstructie blijkt dan:
CD : CE = CG : CF of z : z' = a : a'
waarmee het punt C op BC' kan worden gevonden, met cirkel (B, a). A vinden we dan als snijpunt van de lijn BA' en de liijn door C // A'C'.

A - B, h_a, h_b
	Eerste oplossing Zij ABC de gezochte driehoek ABDE is dan een koordenvierhoek (middelpunt omcirkel is M). Het punt F is zo op de cirkel gekozen, dat ABFE een gelijkbenig trapezium is (EF // AB). Nu geldt: AF = h_b en ook bg(AE) = bg(BF) En ook: DAF = ½bg(DF) = ½bg(BDE - BF - ED) = ½bg(BDE) - ½bg(AE+ED) = A - B. Driehoek AFD kan dus geconstrueerd worden (ZHZ). Waarmee ook de omcirkel (van AFD) en het punt M bekend zijn. Het punt B vinden we als M-spiegelbeeld van A. Het punt E vinden we als tweede snijpunt van de cirkel en lijn door F evenwijdig met AB De lijnen AE en BD geven C.
Tweede oplossing (van Anneke Grünefeld-Raaphorst, in persoonlijke correspondentie)
	Zij ABC de gezochte driehoek. Zij A' zo op AC, dat CA = h_a en B' zo op BC, dat CB' = h_b. Wegens h_a : h_b = b : a zijn dan de driehoeken ABC en A'B'C gelijkvormig (zhz), waardoor A'B' // AB. D ligt nu zo op A'B', dat CD = h_b. Dan is in driehoek A'CD: hoek D = CB'A' = CBA = hoek B en verder ook: A = CA'B'= B + DCA' (buitenhoek van driehoek A'CD), waaruit volgt dat DCA' = A - B Driehoek CDA' is dus te construeren (ZHZ), alsmede driehoek CA'B' waarin dan h_a' de hoogtelijn is op B'C (= BC). De vermenigvuldiging met centrum C en factor h_a / h_a' van driehoek CA'B' geeft dan driehoek CAB.

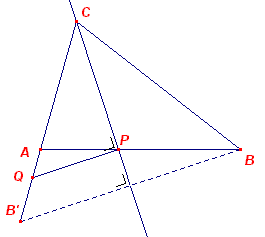
a, b, d_c
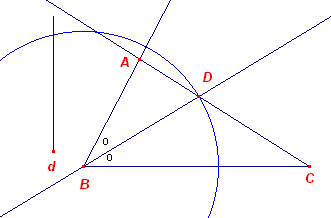
	Zij ABC de gezochte driehoek. Het punt B' op AC is het spiegelbeeld van B in de bissectrice CP. PQ is de lijn // BB' door P. Nu geldt: AP : BP = b : a (bissectrice-stelling) AP : BP = AQ : B'Q (parallel-stelling) terwijl verder AB' = a - b. Het punt Q is nu te construeren. Zie verder de Constructie.
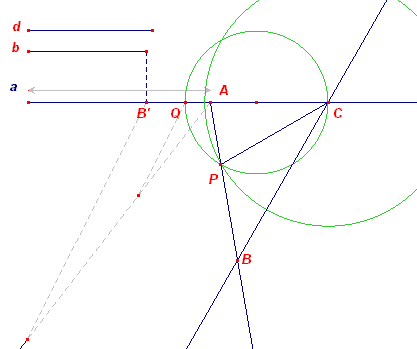	Eerste constructie Maak het lijnstuk AB' gelijk aan a - b en coinstrueer daarop het punt Q in de verhouding b : a. Verleng B'A met een stuk b. Dit geeft het punt C. P ligt nu op de cirkel met middellijn CH (immers hoek P is recht). P ligt ook op de cirkel (C, d). Het punt B ligt op de lijn AP. Het punt B ligt ook op het spiegelbeeld van de lijn AC in CP. De driehoek is geconstrueerd. N.b. Zie hieronder voor een tweede constructie (en evt nog drie andere).

Tweede constructie

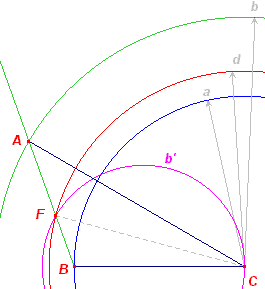Teken drie cirkels met middelpunt C en stralen a, b, d. Deze cirkels geven we aan met hun stralen.

Kiezen we B willekeurig op cirkel a, dan zoeken we nu een punt A op cirkel b zo, dat AB door cirkel d in een punt F gesneden wordt, met de eigenschap BF : AF = a : b

We bekijken de vermenigvuldiging V met centrum B en factor a / (a+b).
V(cirkel b) = cirkel b' is een cirkel die gaat door C, immers voor de afstand p van B (via C) tot de cirkel b geldt:
a / (a+b) · p = a / (a+b) · (a+b) = a
Een der snijpunten van cirkel b' met cirkel d zij F. De (halve) lijn door B en F snijdt cirkel a in A.
Dan is BF = a/(a+b) · BA, of wel BF/ BA = a/(a+b). Zodat:
BF : AF = a : b
Het punt F is dus het gevraagd punt op cirkel d.
ABC is dus de gevraagde driehoek.

¤ Klik hier voor drie andere oplossingen van [ a b d_c ]
¤ Zie eventueel ook Vraag / Antwoord #14472 op WisFaq: "Re: Constructie driehoek" (20 september 2003)

a, B, b - h_a
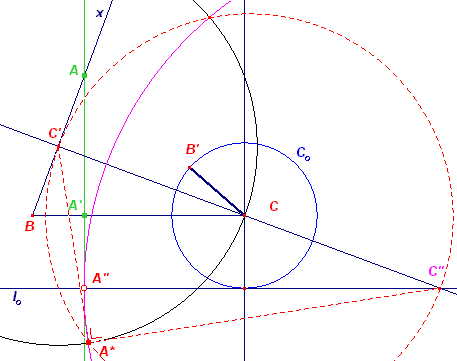
	Probleem - A.P. Hatzipolakis in EHML #8416 (23/10/2003, Hyacinthos nieuwsgroep): "From an old geometry book" Eerste oplossing - N. Dergiades in EHML #8422 (24/10/2003, Hyacinthos nieuwsgroep) - in vertaling: 1. We construeren BC = a, 2. een halve lijn Bx zo, dat de hoek tussen BC en Bx de gegeven hoek is, 3. en cirkel C_o met centrum C en straal d = b - h_a, 4. de raaklijn l_o aan C_o die evenwijdig is met BC. De hoogtelijn AA' snijdt l_o in A" (nog niet te construeren) en de hoogtelijn CC' snijdt l_o in C". 5. De cirkel met middelpunt C' en straal C'C snijdt de cirkel met middellijn C'C" in A. 6. De constructie van A geeft het punt A", omdat C"A" = C"A* en de loodlijn op l_o vanuit A" geeft het derde hoekpunt A van driehoek ABC.
	Toelichting De verklaring is, dat als B' een punt is op AC zo, dat AB' = AA' en C* het spiegelbeeld is van C in Bx, dat dan de cirkel (A, AA') raakt aan BC en aan C_o. Oftewel, de cirkel (A, AC) gaat door C* en C en raakt aan l_o in A". Zodat (C"A")² = (C"C) · (C"C) = (C"A)², of C"A" = C" A* Tweede constructie (Persoonlijke correspondentie met Anneke Grünefeld-Raaphorst, 23-12-2005) Klik hier voor deze constructie.

h_a, h_b, z_a

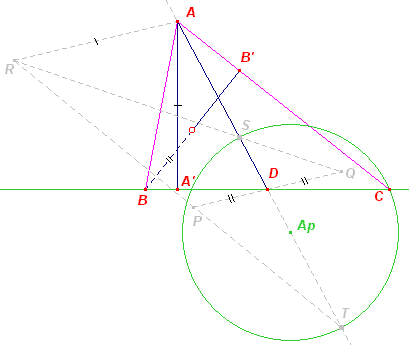Eerste constructie
Driehoek AA'D is direct te construeren (ZZR). Het punt C ligt op de lijn A'D.
Uit h_a · a = h_b · b (= ½Opp(ABC) ) volgt dat de verhouding a : b bekend is.
Nu is CD : CA = ½a : b = ½h_b : h_a.
Het punt C ligt dus ook op de Apollonius-cirkel bij de verhouding ½a : b.

De punten P, Q, R, S, T, Ap zijn gebruikt bij de constructie van die Apollonius-cirkel (klik hier voor deze constructie).
Hierbij is DP = DQ = ½h_b; AR = h_a; AR // PQ, Ap het midden van ST en het middelpunt van de bedoelde Apollonius-cirkel.

Het punt B wordt dan gevonden door puntspiegeling van C in D.
Waarmee de driehoek geconstrueerd is.

Tweede constructie
(Persoonlijke correspondentie met Anneke Grünefeld-Raaphorst, 30-11-2005)
Klik hier voor deze constructie.

h_a, h_b, h_c
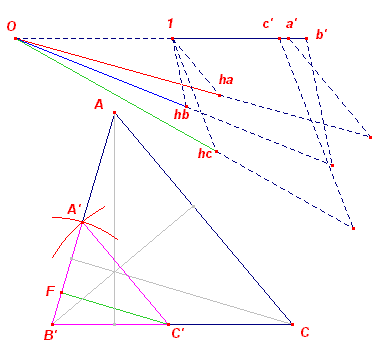	Voor de oppervlakte S van een driehoek geldt: S = ½h_a · a = ½h_b · b = ½h_c · c Hieruit volgt a : b : c = 1/h_a : 1/h_b : 1/h_c We kunnen nu dus een driehoek A'B'C' construeren (ZZZ) die gelijkvormig is met de gevraagde driehoek. In het bovenste deel van de figuur hiernaast zijn lijnstukken a', b', c' geconstrueerd op basis van de gegeven lengtes van h_a, h_b en h_c. Hierbij is gebruik gemaakt van een lijnstuk met de lengte 1. Uit driehoek A'B'C' is daarna driehoek AB'C ontstaan door vermenigvuldiging met centrum B' en factor h_c / CF (de hoogtelijn uit C in driehoek A'B'C'). Opmerking. Zie ook [ h_a, h_b, r ].
d_a, h_a, z_a
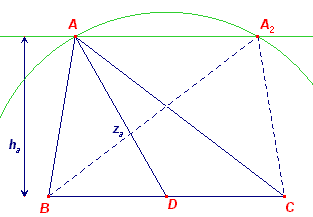
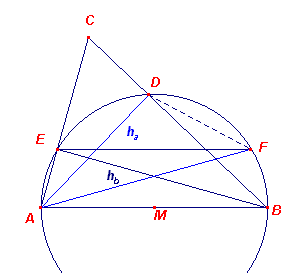
	Op basis van de gegeven lijnstukken kan driehoek AEF worden geconstrueerd (ZZR). Het punt D ligt op de lijn EF. D is te vinden als snijpunt van de cirkel (A, z_a) met EF. De bissectrice AE snijdt de omcirkel in het midden van bg(BC). De loodlijn in D op BC snijdt de omcirkel in hetzelfde punt. Dit geeft dus A'. Het middelpunt O van de omcirkel is het snijpunt van de middelloddlijn van AA' en de lijn A'D. De punten B en C worden gevonden als snijpunten van de omcirkel met de lijn EF.

3. Constructies met om- en/of incirkel

N.b.
- R is de straal van de omcirkel (omgeschreven cirkel) van driehoek ABC;
- r is de straal van de incirkel (ingeschreven cirkel) van driehoek ABC.

a, b, R
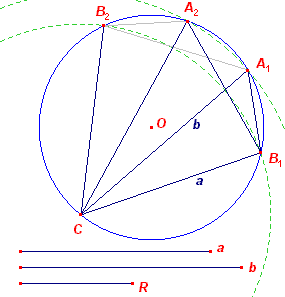	Construeer een cirkel (O, R), met daarin twee koorden met lengtes a en b met als gemeenschappelijk eindpunt het punt C. We vinden dan in het algemeen twee verschillende driehoeken ABC.

a, h_b, r
	Klik hier voor de constructiebeschrijving.

A, a, h_a
	De meetkundige plaats van het punt A bij gegeven zijde a kan worden gevonden met de stelling van de omtrekshoek. De lijn evenwijdig met BC op afstand h snijdt deze boog in 0, 1 of 2 punten, waarmee het (een) punt A gevonden is.

A, a, r
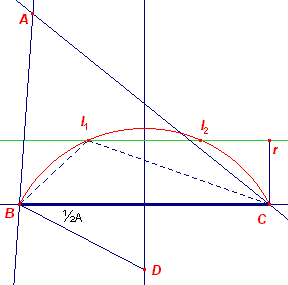	Bij deze constructie kan gebruik gemaakt worden van de meetkundige plaats van de punten waaronder een lijnstuk (in dit geval a) wordt gezien onder een gegeven hoek (stelling van de omtrekshoek). Zij I het incentrum van ABC, dan is BIC = 180 - ½(B + C) = 180 - ½(180 - A) = 90 + ½A De meetkundige plaats van I kunnen we dus bepalen. I ligt verder op een lijn m evenwijdig met BC op een afstand r van BC. Waarmee I en daarmee de lijnen BI en CI gevonden zijn. Spiegeling van de lijn BC in die lijnen geeft dan het punt A. Constructie In de figuur hiernaast is A gegeven door ½A, geplaatst in B. D (op de middelloodlijn van BC) is het middelpunt van een cirkelboog die de meetkundige plaats van het punt I vormt. De lijn m snijdt deze meetkundige plaatst in de punten I₁ en I₂. Opmerking - Zie ook de constructie [ A R r ].
A, a, r_a
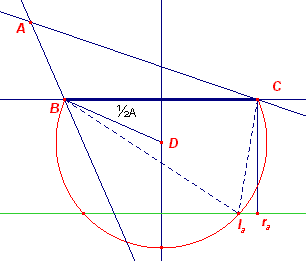	De constructie verloopt analoog als we r_a in plaats van r kiezen. De meetkundige plaats van I_a is dan het andere deel van de cirkel met middelpunt D.
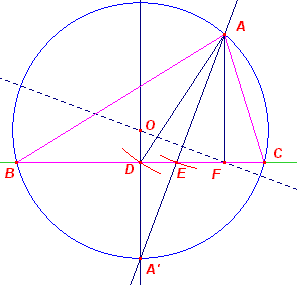
A, a, d_a
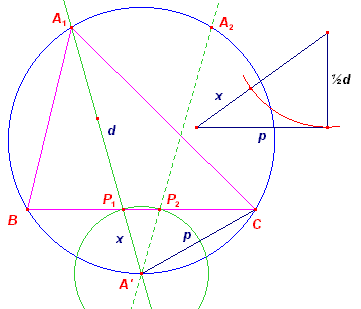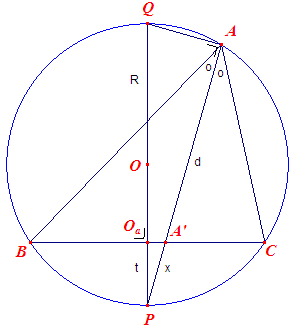
	Zij ABC de gezochte driehoek. De bissectrice van A snijdt de omcirkel (die construeerbaar is bij gegeven A en a) in het punt A', en de drager van BC in P. Zij nu A'P = x en A'C = p. p is nu bekend. Nu is verder AA'C ~ CA'P, waaruit volgt: AA' : CA' = A'C : A'P of (x + d)x = p² Uitgewerkt: x² + dx = p² (x + ½d)² = p² + (½d)² Het lijnstuk z met z² = p² + (½d)² is nu construeerbaar (stelling van Pythagoras). Zodat x = z - ½d Via de cirkel (A', z - ½d) is dus het punt P op BC te vinden en het tweede snijpunt van de lijn A'P met de omcirkel is het [unt A.

A, a - b, r / A, b + c, r
________________________	Bij deze constructies wordt gebruik gemaakt van de projectie van het punt I op een geschikte zijde van de basisdriehoek. Klik hier voor de constructiebeschrijvingen.

A, R, r

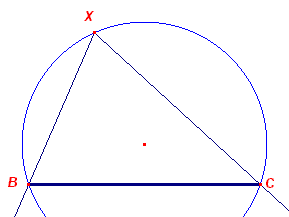Deze constructie kan worden teruggebracht tot de constructie [ A a r.].
Immers, de cirkel met straal R bepaalt samen met de hoek A de lengte van het lijnstuk BC = a.
Constructie
Teken een cirkel met straal R en daarop een willekeurig punt X.
Teken twee halve lijnen l en m met Ð(l, m) = A.
De tweede snijpunten van de lijnen l en m met de cirkel zijn dan de punten B en C.
Zie verder dus [ A a r.].

a, d_a, R
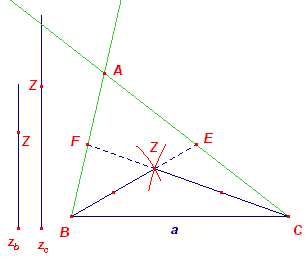
	Stel het probleem is opgelost. De middelloodlijn van BC snijdt BC in het punt O_a en de omcirkel in P en Q. De bissectrice van A snijdt de omcirkel eveneens in P en BC in A'. Nu is PAQ = 90° (Thales-cirkel), zodat PAQ ~ PO_aA' (immers beide driehoeken hebben APQ gemeenschappelijk). Dus: PA' / PO_a = PQ / PA Is nu x = PA' , PO_a = t en d_a = d dan staat hier: x / t = 2R / (x + d) waarin alleen x onbekend is. Dus: x(x + d) = t · (2R) En hieruit is x te construeren (zie onderstaande constructie). En daarna vinden we eenvoudig driehoek ABC.
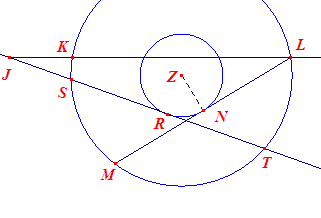	Kies op een halve lijn door J de punten K en L met JK = t en JL = 2R. Kies op een ahlve lijn door L een punt M met LM = d Z is het middelpunt van de omcirkel van KLM. ZN is is de afstand van Z tot LM. Teken daarna een raaklijn aan de cirkel (Z, ZN), die de omcirkel van KLM snijdt in de punten S en T. Nu is JS = x. Bewijs De koorden LM en ST liggen op gelijke afstand van Z. Dus LM = ST = d Er geldt m(J) = JK · JL = t · (2R) Ook m(J) = JS · JT = JS · (JS + ST) = JS · (JS + d) Dus JS voldoet inderdaad aan x · (x + d) = t · (2R)

a - b, h_a, r

Z is de projectie van I op AB. Z_c is de projectie van I_c (middelpunt van de C-uitcirkel van ABC) op AB.
Wegens
ZZ_c = AB - AZ - BZ_c = c - 2(s - a) = c - (a + b + c) - 2a = a - b
is driehoek IZZ_c te construeren (ZHZ).
De punten A en B liggen op de lijn ZZ_c.
Het midden M_c van BC is dus ook het midden van ZZ_c.
De loodlijn op BC vanuit M_c is gelijk aan ½h = ½h_a (middenparallel).
BC is dus een gemeenschappelijke (uitwendige) raaklijn aan de cirkels (I, r) en (M_c, ½h).
De raakpunten zijn dan V en U. Dit geeft dan op de lijn ZZ_c het punt B.
A is dan de gespiegelde van B in het punt M_c.
De tweede raaklijn uit A aan de cirkel (I) geeft dan samen met de lijn BU het punt A.

a + b, A - B, r_a + r_b	>> b + c, B - C, r_b + r_c
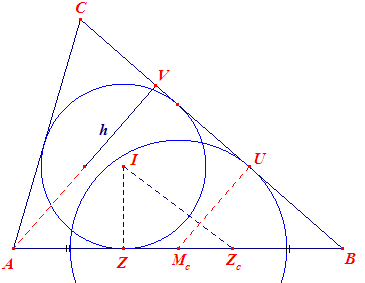
______________________	Bij deze constructie wordt gebruik gemaakt van de projecties X_b en X_c van de punten I_b en I_c op de zijde BC van de basisdriehoek. Daarbij is: X_bX_c = b + c. De hoek ½(B-C) is de hoek tussen de lijn I_bI_c en de zijde BC van de driehoek. Klik hier voor de constructiebeschrijving.

h_a, h_b, r

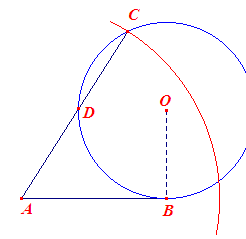Een bekende formule is: 1 / r = 1 / h_a + 1 / h_b + 1 / h_c
Uit de gegevens kunnen we dan, mits we de omgekeerde van een lijnstuk kunnen construeren, de derde hoogtelijn (in dit geval h_c) vinden.
Dan is de constructie teruggebracht tot [ ha, hb, hc ].

Omgekeerde van een lijnstuk
Gegeven: x
Te construeren: 1/x
Constructie:
Beschikken we over een lijnstuk AB met lengte 1, dan is deze constructie mogelijk.
O is het middelpunt van een cirkel die in B raakt aan AB.
C is een punt op die cirkel met AC = x.
Dan is: AB² = AC · AD, waaruit dus volgt dat AD = 1/x.

4. Bijzondere constructies

A, X, X_a
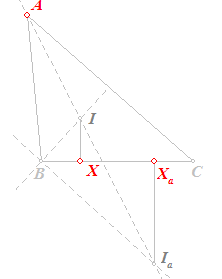	X en X_a zijn de projectes van opvolgend I en I_a op de zijde BC van driehoek ABC. De punten A, X en X_a zijn in ligging gegeven. Bij deze constructie wordt gebruik gemaakt van de harmonische ligging van vier punten op een lijn. Klik hier voor de constructiebeschrijving.

O, H_a, D_a
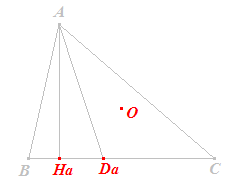	O - middelpunt van de omcirkel (omgeschreven cirkel van de driehoek) H_a - voetpunt van dehoogtelijn uit A D_a - snijpunt van de binnenbissectrice van A en de zijde BC Deze punten zijn in ligging gegeven. Klik hier voor de constructiebeschrijving.
Probleemstelling: Ricardo Barroso EHML (Hyacinthos nieuwsgroep), #11121 (26-03-2005) Subject: A construction problem with circumcenter and two feet; (later gewijzigd in) Construction of a triangle given O and feet of altitude and bisector on a side.

z_a, r, r_a
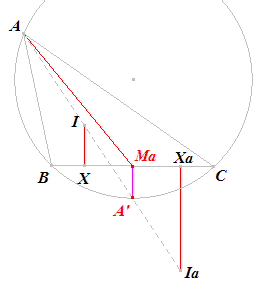	Bij deze constructie gebruik gemaakt van -- de harmonische ligging van vier punten op een lijn, en -- de grootte van het lijnstuk M_aA', waarbij M_a het midden is van de zijde BC ( = a) en A' het snijpunt van de bissectrice van A met de omcirkel van ABC. Klik hier voor de constructiebeschrijving en de bijbehorende theorie.

[drieconstr.htm] laatste wijziging op: 24-12-05