Volledige vierzijde en dubbelverhouding
Overzicht ][ Stralenbundels | Transversalen | Meetkunde
| Definitie De figuur bestaande uit vier elkaar snijdende lijnen en hun snijpunten heet volledige vierzijde. |
We hebben in de hieronder staande figuur 1:
| figuur 1 | 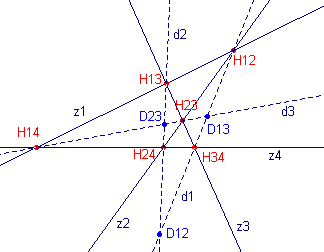 |
zijden: z1, z2, z3, z4 hoekpunten: H12, H13, H14, H23, H24, H34 overstaande hoekpunten: het paar H12, H34, het paar H13, H24, het paar H14, H23 diagonalen: dit zijn lijnen door overstaande hoekpunten, dus d1, d2, d3 De figuur gevormd door de diagonalen heet diagonaal-driezijde met (diagonaal-)hoekpunten D12, D13 en D23. |
| Definitie De figuur bestaande uit vier punten en hun verbindingslijnen heet volledige vierhoek. |
We hebben in de hieronder staande figuur 2:
| figuur 2 |  |
hoekpunten: A1, A2, A3, A4 zijden: m12, m13, m14, m23, m24, m34 overstaande zijden: het paar m12, m34, het paar m13, m24, het paar m14, m23 diagonaalpunten: D1, D2, D3 diagonaal-driezijde (niet in de figuur): d12 (door D1 en D2), d13 (door D1 en D3), d23 (door D2 en D3) |
De zogenoemde duale samenhang tussen beide vinden we terug in het onderstaande overzicht:
| volledige vierzijde | volledige vierhoek | |
| zijden: z1, z2, z3, z4 | hoekpunten: H1, H2, H3, H4 | |
| hoekpunten: H12, H13, H14, H23, H24, H34 | zijden: m12, m13, m14, m23, m24, m34 | |
| diagonalen: d1, d2, d3 | diagonaalpunten D1, D2, D3 | |
| hoekpunten diaogonaal-driehoek: D12, D13, D23 | zijlijnen diagonaal-driezijde d12, d13, d23 |
We zien hieruit een 1-1-correspondentie tussen de begrippen punt en lijn.
Om deze dualiteit op te heffen kunnen eigenschappen "P ligt op de lijn l" en "l gaat door het punt P" vervangen door "het punt P en de lijn l zijn incident".
2.
Dubbelverhouding en harmonische ligging ![]()
Van twee punten C en D op de lijn door de punten A en B is de ligging bepaald door de
beide deelverhoudingen (ABC) en ABD; zie figuur3.
| figuur 3 | 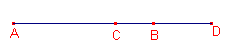 |
| Definities [1] Onder de dubbelverhouding van de punten A,B en C,D verstaan we het getal (ABCD) = (ABC)/(ABD). [2] Als (ABCD) = -1, dan zeggen we dat het puntenpaar A, B harmonisch ligt met het puntenpaar C, D. |
Gevolg
(ABCD) = CA/CB : DA/DB
[einde Gevolg]
Voorbeelden
| figuur 4 | 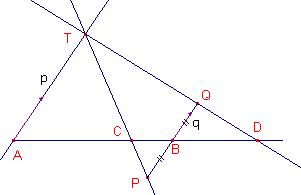 |
[1] In driehoek ADT is BQ evenwijdig met AT en is BP=BQ. De punten A, B, C, D is nu een harmonisch puntenviertal. Bewijs: Stel BP = q en AT = q. |
Opmerking
Op bovenstaande eigenschap kan een constructie van de vierde harmonisch bij
drie collineaire punten worden gebaseerd.
Klik hier voor een beschrijving van die
constructie.
[einde Opmerking]
| figuur 5 | 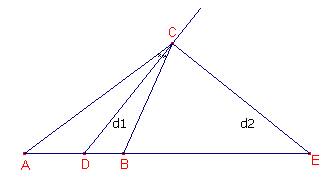 |
[2] De binnen- en buitenbissectrice van een hoek van een driehoek leggen samen met de hoekpunten op de overstaande zijde een harmonisch puntenviertal vast. Bewijs: DA / DB = - b / a en EA / EB = b / a. |
[einde Voorbeelden]
Gevolg van de definitie
Voor het midden C van een lijnstuk AB geldt: (ABC) = -1. Voor de
dubbelverhouding (ABCD) met een vierde harmonisch punt D geldt (ABCD) = -1.
Hieruit volgt: (ABD) = 1.
Het punt D is dan het oneigenlijk punt van de lijn AB.
Dus:
Het midden van een lijnstuk en het oneigenlijk punt van de drager van dat lijnstuk
liggen harmonisch met de eindpunten van het lijnstuk.
[einde Gevolg]
Bewijs (zie figuur 6):
| figuur 6 | 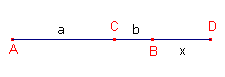 |
Stel AC = a, BC = b met a > b. Stel nu BD = x. Nu volgt uit (ABCD) = -1 dat a / b = (x + a + b) / x of (a - b) x = ab + b2 |
We onderscheiden:
(i) a <> b.
Nu kunnen we x uniek bepalen uit bovenstaande relatie: x = (ab + b2)/(a-b)
(ii) a = b.
In dit geval is C het midden van het lijnstuk AB. D is dus het oneigenlijk punt van het
lijnstuk AB. ¨
| Stelling 2 Twee diagonalen van een volledige vierzijde scheiden de hoekpunten op de derde diagonaal harmonisch. |
Bewijs:
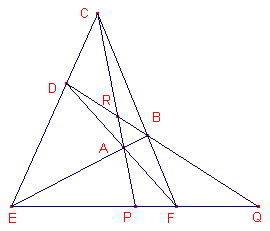 |
AB, BC, CD, DA zijn de zijden van een volledige vierzijde. E = AB /\ CD, F = BC /\ DA. We moeten nu bewijzen, dat de hoekpunten E en F harmonisch gescheiden worden door de diagonalen AC en BD. Zij verder P = AC /\ EF, Q = BD /\ EF, dqan moet dus gelden (EFPQ) = -1. Uit de stelling
van Menelaos en Ceva, toegepast op driehoek CEF met transversaal DBQ volgt: |
Opmerking
Stelling 2 staat ook (als Stelling 3 ) op de pagina "Stralenbundels".
Zie verder ook de pagina "Harmonikaal".
[einde Opmerking]
Overzicht
3.1. Het harmonisch gemiddelde
3.2. Het midden van een lijnstuk
3.3. Loodrecht snijdende cirkels ![]()
3.1. Het harmonisch gemiddelde ![]()
| figuur 7 |  |
Zie figuur 7.
Uit (ABCD) = -1 volgt (per definitie) (ABC)/(ABD) = -1, of (ABC) + (ABD) = 0.
Dus CA/CB + DA/DB = 0, waaruit we vinden: CA.DB + CB.DA = 0.
Herschrijving geeft:
CA(AB-AD) + DA(AB-AC) = 0
CA.AB - CA.AD + DA.AB - DA.AC = 0, waarbij CA.AD = AC.DA
CA.AB + DA.AB = 2 CA.AD of AC.AB + AD.AB = 2 AC.AD
Deling door AB.AC.AD geeft dan
1/AD + 1/AC = 2/AB.
1/AB is dus het rekenkundig gemiddelde van 1/AD en 1/AC. ¨
In dit geval noemen we AB het harmonisch gemiddelde van AC en AD.
3.2. Het midden van een lijnstuk ![]()
| figuur 8 | 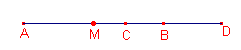 |
Zie figuur 8.
Voor het midden M van een lijnstuk AB geldt MA = - MB.
In 3.1 hebben we gevonden
AC.DB = AD.CB = 0, zodat
(MC-MA)(MB-MD) + (MD-MA)(MB-MC) = 0
(MC-MA)(MA+MD) + (MD-MA)(MA+MC) = 0
waaruit volgt
MC.MD = MA2
en dus ook MB2 = MC.MD ¨
3.3 Loodrecht snijdende cirkels ![]()
| figuur 9 | 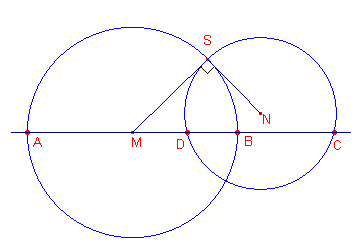 |
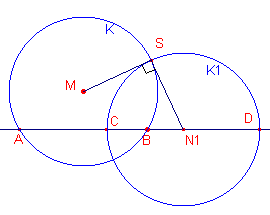
We gaan uit van twee elkaar loodrecht in S snijdende cirkels (zie
figuur 9). Bekijken we de macht van het punt M ten opzichte van cirkel C2. Nu is MS2 = MD.MC En dus ook, wegens MA = MS, MA2 = MD.MC A,B,C,D is dus een harmonisch viertal. Omgekeerd. |
Opmerkingen
[1]
Eigenschap 3.3, en het omgekeerde ervan, is als stelling geformuleerd in de volgende
paragraaf.
[2]
Van die stelling wordt in de volgende paragraaf ook een animatie
gegeven. ![]()
[einde Opmerkingen]
4.
Apollonius-cirkels en harmonische ligging ![]()
Voor de definitie van een Apollonius-cirkel van een driehoek zie de pagina over Apollonius-cirkels.
Bewijs: zie paragraaf 3, Overige eigenschappen, eigenschap 3.3. ¨
En een gevolg hiervan is weer een stelling die ook wordt genoemd op de pagina over Apollonius-cirkels.
| Stelling 4 De Apollonius-cirkels van een driehoek snijden de omgeschreven cirkel van een driehoek loodrecht. |
[einde Gevolg]