Stralenbundels

Overzicht  ][  Vierzijde  |  Transversalen   |  DK & Meetkunde

Overzicht terug

  1. Definities en stellingen
  2. Constructies
  3. Harmonische vierhoek

1. Definities en stellingen terug

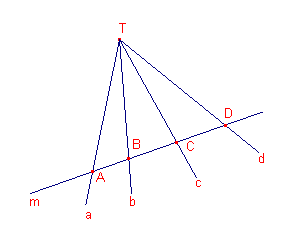figuur 1  stral1
Definities
[1] Een stralenbundel (ook wel lijnenbundel genoemd) is een verzameling lijnen (niet noodzakelijk oneindig veel) die door één punt gaan.
De lijnen worden ook wel stralen genoemd. Het punt heet de top van de stralenbundel.
[2] Een stralenbundel bestaande uit vier stralen heet vierstraal.
[3] Een transversaal van een stralenbundel is een lijn die niet door de top van de stralenbundel gaat en alle lijnen van de bundel snijdt.
[4] Onder de dubbelverhouding T(abcd) van vier lijnen a, b, c, d in een stralenbundel (met top T) verstaan we de dubbelverhouding (ABCD) waarbij A,B,C,D de snijpunten zijn van opvolgend a,b,c,d met een transversaal van de bundel.
Dus: T(abcd) = (ABCD).
[5] Een vierstraal a,b,c,d met T(abcd) = -1 heet harmonische vierstraal.
De harmonische vierstraal wordt ook zelf wel aangegeven met T(abcd) of met T(ABCD).
Stelling 1
T(ABCD) is een vierstraal.
Voorts is l de lijn door B evenwijdig met de toegevoegde straal (de straal door A). l snijdt de beide andere stralen in de punten P en Q.
T(ABCD) = -1 desda PB= BQ

Bewijs:
Zie figuur 2.

figuur 2  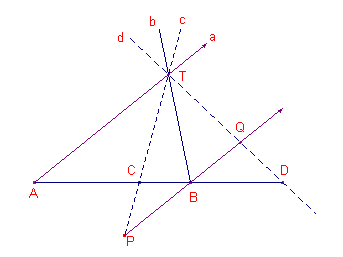stral2 Als T(ABCD) = -1, dan is (volgens de definitie) ook (ABCD) = -1.
Stel dan AC = a en BC = b. Dus is AD = ka en BD = kb.
   BQ : TA = kb : ka = b : a
   BP : TA = b : a
Waaruit volgt dat BP = BQ.
Omgekeerd.
Zij BP = BQ.
Nu is BP : TA = BC : AC = b : a.
Dus, wegens BP = BQ, hebben we BQ : TA = b : a, dus ook BD : DA = b : a
Hieruit volgt dan BD = kb en DA = ka, zodat
   (ABCD) = CA/CB : DA/DB = (-b/a) : (kb/ka) = -1. ¨
Stelling 2
Twee snijdende rechten a, b worden door de bissectrices c, d van de hoeken die ze met elkaar maken, harmonisch gescheiden.

Bewijs:

figuur 3  stral3 Zie figuur 3.

Trek de lijn l evenwijdig met a.
l snijdt b, c, d opvolgend in B, C, D.
In driehoek CTB is hoek C = hoek C; in driehoek CDT is hoek D = hoek T.
Beide driehoeken zijn dus gelijkbenig, zodat CB = CT = CD.
Volgens stelling 1 is dus T(abcd) = -1. ¨

Gevolg
Als van de harmonische vierstraal T(abcd) de stralen c en d loodrecht op elkaar staan, dan delen ze de hoeken tussen a en b middendoor.
[einde Gevolg]
Stelling 3
Twee diagonalen van een volledige vierzijde scheiden de hoekpunten op de derde diagonaal harmonisch.

Bewijs: (zie figuur  4)

figuur 4  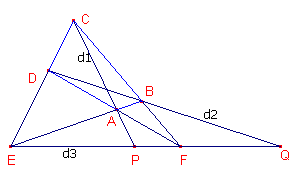stral4 ABCDEF is de volledige vierzijde (AB,BC,CD, DA).
AC en BD zijn opvolgend de 1e en de 2e diagonaal. EF is de 3e diagonaal.
Te bewijzen is nu dat (EFPQ) = -1.

In driehoek CEF passen we de stelling van Menelaos toe op de transversaal DBQ.
Nu is (CED)(EFQ)(FCB) = 1.
Door A gaan drie hoektransversalen in dezelfde driehoek.
Volgens de stelling van Ceva is dan
   (CED)(EFP)(FCB)= -1.

Dus, na deling van beide resultaten: (EFP)/(EFQ) = -1 of PE/FE : QE/QF = (EFPQ) = -1. ¨

Opmerking
Zie verder ook de pagina "Harmonikaal".
[einde Opmerking]

2. Constructies terug
Op basis van stelling 1 en stelling 3 in paragraaf 1 kunnen we nu een tweetal verschillende constructies geven voor de vierde harmonische bij drie gegeven collineaire punten.

1e Constructie

figuur 5  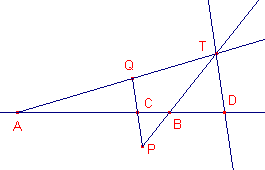stral5 Zie figuur 5.

Gegeven zijn de punten A, B, C, met C tussen A en B (dus op het lijnstuk AB).
(1) Kies het lijnstuk PQ door C met PC = QC.
(2) Trek AQ.
(3) Trek BP; bepaal het snijpunt T van AQ en PB.
(4) Trek TD evenwijdig met PQ (D op de lijn AB).

Klik hier Animatie voor een stapsgewijze animatie van deze constructie.

Opmerkingen
[1] Voor het bewijs van deze constructie zie stelling 1.
[2] Bij deze constructie moet gebruik gemaakt worden van passer en liniaal.
[einde Opmerkingen]

2e constructie

figuur 6  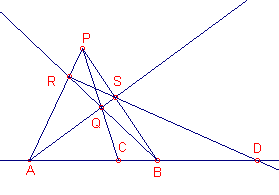stral6 Zie figuur 6.

Gegeven de punten A, B, C met C tussen A en B.
(1) Kies punt P buiten de lijn AB.
(2) Trek PA, PB, PC.
(3) Kies Q op PC.
(4) Trek BQ en bepaal R op PA.
(5) Trek AQ en bepaal S op PB.
(6) Trek RS en bepaal D op AB.

Klik hier Animatie voor een stapsgewijze animatie van deze constructie.

Opmerkingen
[1] Voor het bewijs van deze constructie zie stelling 3.
[2] Bij deze constructie is alleen gebruik gemaakt van een liniaal.
[einde Opmerkingen]

3. Harmonische vierhoek terug

Definitie
Een harmonische vierhoek is een koordenvierhoek waarvan de producten van de overstaande zijden gelijk zijn.
Stelling 4
Een harmonische vierstraal T(abcd) waarvan T op een cirkel ligt, bepaalt op die cirkel een harmonische vierhoek ABCD, waarbij A, B, C, D de snijpunten zijn van de stralen met de cirkel).

Bewijs:

figuur 7  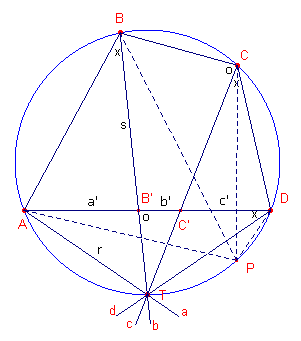stral7 Zie figuur 7.

We kiezen de lijn door A en D als transversaal van de vierstraal. De lijnen b en c snijden AD in B’ en C’.
Nu is A, C’, B’, D een harmonisch viertal.
Voor een willekeurig punt P van de cirkel hebben we nu
   P(a’b’c’d’) = T(abcd) = -1.
De beide vierstralen zijn dus congruent. We doen dus de algemeenheid niet te kort door de vierstraal zo te kiezen, dat T op de middelloodlijn van AD ligt.

De lengten van de zijden van vierhoek ABCD geven we (mogelijk wat verwarrend) ook aan met a, b, c, d.
Zij AB’ = a’, B’C’ = b’, C’D = c’, TA = TB = r, TB   = s
Nu is
TAB’ ~ TBA, immers hoek A in TAB’ is gelijk aan hoek B in TBA (staande op dezelfde boog) en hoek T is gemeenschappelijk.
Dus: AB’ : BA = TA : TB en dus a’ : a = r : s.

Om dezelfde reden hebben we
TDC’ ~ TCD, waaruit volgt:
   DC’ : CD = TC’ : TD, zodat c’ : c = TC’ : r
Door vermenigvuldiging volgt uit deze laatste resultaten, dat a’c’ : ac = TC’ : r.
Duidelijk is dat TB’C’ ~ TCB, zodat B’C’ : CB = TC’ : TB, waaruit b’ : b = TC’ : s.
Combinatie hiervan met het vorige resultaat geeft:
   a’c’ : ac = b’ : b = b’d : bd.
Uit (AC’B’D) = B’A/B’C’ : DA/DC’ = -a’ / b’ : (-d) / (-c’) = -1, vinden we a’c’ = b’d.
Dit samen met het vorige resultaat geeft
   ac = bd.
De producten van de overstaande zijden zijn gelijk. Dus is ABCD een harmonische vierhoek. ¨

Opmerking
Volgens de stelling van Ptolemaeus is dus ac = bd = ½ pq, waarbij p en q de lengtes zijn van de diagonalen van de koordenvierhoek.
[einde Opmerking]

begin pagina
[stralenb.htm] laatste wijziging op: 02-03-2004