Driehoeksconstructies: a, b, A - B en a, B - C, ha

Constructies ][ Driehoeksconstructies | Meetkunde | Cabri

Overzicht constructies

[ a b A - B ]

[ a B - C ha ]

a, b, A - B >> b, c, B - C

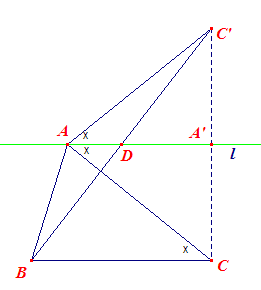Veronderstel dat de constructie is uitgevoerd.

De lijn l is de lijn door A evenwijdig met BC. C' is het spiegelbeeld van C in l.
Dan is:
   BAA' = 180 - B
   C'AA' = CAA' = C
   BAC' = BAA' + C'AA' = 180 - B + C = 180 - (B - C)
Met AB = c, AC' = AC = b en hoek BAC'kan nu driehoek ABC' worden geconstrueerd (ZHZ).
l is middenparallel in driehoek BCC'.
Dus AD is construeerbaar met D als midden van BC.
En C is het spiegelbeeld van C' in l.

Opmerking
Door de constructie [a, b, A - B] uit te voeren als [b, c, B - C] wordt de constructie [a, B-C, ha] daarmee in overeenstemming gebracht.

Tweede constructie [ b, c, B - C ]
	Construeer op de drager van BA (= c) het lijnstuk b + c (verleng BA met AD = b). Nu is: BCD = BCA + ACD = C + ½A = ½C + ½C +½A + ½B - ½B = 90 - ½(B - C) = p Dus C ligt op bg(p, BD); omtrekshoek. De ligging van A en B (op BD) is bekend. C ligt ook op de cirkel (A, b), waarmee ook C te construeren is.

a, B - C, h_a

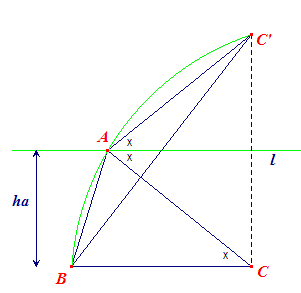Veronderstel dat de constructie is uitgevoerd.

De lijn l is de lijn door A evenwijdig met BC. C' is het spiegelbeeld van C in l.
Zoals we hierboven, bij de constructie van [a, b, A-B], hebben gezien, is nu:
BAC' = 180 - (B - C)
We kunnen de punten B, C en C' met behulp van h_a en de lijn l construeren, immers l ligt op een afstand h_a van BC.
Dan is ook het lijnstuk BC' bekend.
Het punt A ligt dan op de boog BC', behorend bij de koorde BC' die de hoek BAC' onderspant.
Maar A ligt ook op l.
We vinden A dus als snijpunt van beide.

[p : a_b_a-b.htm ] laatste wijziging op: 21-04-2005