Driehoeksconstructie: A, b + a, c + a

[  Driehoeksconstructies | Meetkunde | Cabri  ]

[ Terug naar de pagina Driehoekconstructies ]

A, b+a, c+a

We behandelen hier een andere constructie dan die gegeven is op de pagina "Driehoeksconstructies".
Deze constructie is gedeeltelijk gebaseerd op projectieve eigenschappen van de figuur.

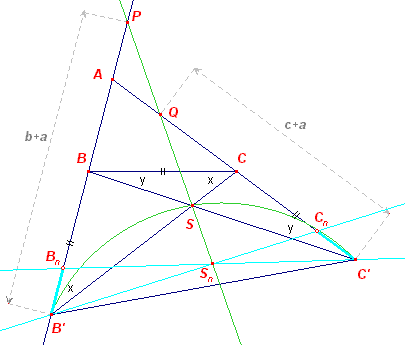abpacpa Driehoek AB'C' is op basis van de gegeven lijnstukken direct te construeren (ZHZ).

Zij S nu het snijpunt van B'C en C'B als ABC de gezochte driehoek is.
Is verder BB'C = x en CC'B = y, dan is ook:
A + B + C = 180, B = 2x (buitenhoek van BB'C), C = 2y (buitenhoek van CC'B)
Zodat A = 180 - 2x - 2y, of ½A = 90 - x - y
Voor B'SC' hebben we dan (in BSC):
   B'SC' = 180 - x - y = 90 + (90 - x - y) = 90 + ½ A.
De meetkundige plaats van het punt S is daardoor bekend (stelling van de omtrekshoek): een cirkelboog.

We kiezen nu op B'A en C'A opvolgend de punten Bn en Cn, met B'Bn = C'Cn.
Deze punten vormen twee projectieve puntreeksen.
De stralenbundels van de lijnen B'Cn en C'Bn zijn dus eveneens projectief.
Echter B'C' is een gemeenschappelijke straal van deze bundels, waaruit volgt dat de bundels perspectief zijn.
De snijpunten, Sn, van overeenkomstige stralen zijn daardoor collineair.
De collineatie-as is de lijn PQ in nevenstaande figuur.

Het punt S is zo'n snijpunt van overeenkomstige stralen. S ligt dus ook op PQ.
We kunnen de punten P en Q (en daarmee de lijn PQ) construeren door het lijnstuk b+a vanuit B' af te zetten langs B'A, en het lijnstuk c+a vanuit C' langs C'A.

S is dus het snijpunt van de bedoelde meetkundige plaats (de cirkelboog) en de lijn PQ.

[ Terug naar de pagina Driehoekconstructies ]

begin pagina
[abzc.htm] laatste wijiging op 26-10-03