Driehoeksconstructie: za, r, ra

Theorie  |  Constructie   |  Referenties  ][  Driehoeksconstructies   |   Meetkunde   |  Cabri

Theorie terug

za, r, ra  
Bij de constructie maken we gebruik van:
- de harmonische ligging van vier punten op een lijn (zie Lemma 1);
- een eigenschap van de omcirkel van een driehoek (zie Lemma 2).
Lemma 1 terug
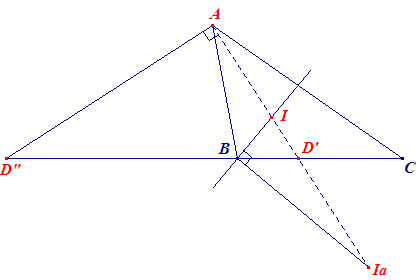zarra1 In ABC zijn AD' en AD" de binnen- en buitenbissectrice van hoek A.
Volgens de bissectricestelling (zie Referenties) hebben we:
  BD' : CD' = BA : CA
  BD" : CD" = BA : CA
zodat
  BD' : CD' = CD' : CD"
en dus
  BD' / BD" = CD' : CD" = (D'D"BC) = -1
De puntenparen [D', D"] en [B, C] zijn dus harmonische puntenparen op de lijn BC.
Zodat:
Dus:
De binnen- en buitenbsissectrice van een hoek snijden de overstaande zijden in punten die harmonsich liggen tov. de hoekpunten op die zijde.

Gevolg
In driehoek ABD' zijn BI en en BIa binnen- en buitenbiseectrice van hoek B. Zodat:

Lemma 1. De puntenparen [A, D'] en [I, Ia] zijn harmonische puntenparen op de binnenbissectrice van hoek A van driehoek ABC.

N.b.
Zie de paragraaf "Referenties" voor een uitvoeriger behandeling van eigenschappen samenhangend met dit lemma.

Lemma 2 terug
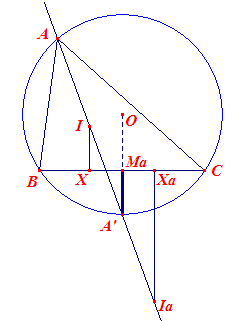zarra3 Zie nevenstaande figuur.
Daarin is IX = r en IaXa = ra.
Het punt A' is het snijpunt van de bissectrice van hoek A met de omcirkel (middelpunt O).
Het punt Ma is het midden van BC (en van XXa).

Lemma 2. MaA' = ½(ra - r)

N.b.
Zie de paragraaf "Referenties" voor een uitvoeriger behandeling van eigenschappen samenhangend met dit lemma.

Constructie terug

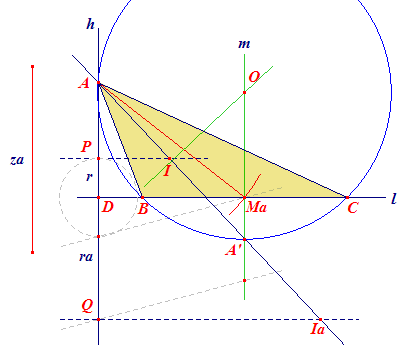zarra4 Constructiebeschrijving
Construeer op een (horizontale) lijn l in een punt D een loodlijn h met daarop aan verschillende kanten van D de punten P en Q, zo, dat DP = r en DQ = ra.
Construeer op h het punt A, met (ADPQ) = -1 (met de constructie van de vierde harmonische).
Door projectie evenwijdig aan l op de bissectrice van hoek A van driehoek ABC gaan deze punten opvolgend over in A, I, D' en Ia (waarbij D' het snijpunt is van de bissectrice van hoek A met de lijn l, die later ook de punten B en C zal dragen). Immers, dubbelverhoudingen zijn invariant bij evenwijdige projectie; zie Lemma 1.
De cirkel A(za) snijdt de lijn l in het midden Ma van BC. De lijn AMa is dus de zwaartelijn uit A van driehoek ABC.
Construeer in Ma een loodlijn m (de middelloodlijn van BC) op l en bepaal daarop het punt A' met MaA' = ½(ra - r); zie Lemma 2.
De omcirkel van ABC gaat door A en A'. Het middelpunt O daarvan ligt dus op m en op de middelloodlijn van AA'.
De snijpunten van O(OA) met de lijn l zijn de punten B en C.

Referenties terug
Een uitvoeriger toelichting bij bovenstaande lemmata is te vinden in:

[1]       N. A. COURT: College Geometry. Barnes & Noble (1952)
[2] DICK KLINGENS: Over de tritangent stralen van een driehoek. PDF-bestand (maart 2004), ca. 215 kB
[3] Bissectricestelling; zie pagina "Transversalen" (op deze website).
[4] Constructie van de vierde harmonische; zie pagina "Stralenbundels" (op deze website).
[5] Uitcirkels; zie pagina "Uitcirkels" (op deze website).

begin pagina
[p : z_arr_a.htm] laatste wijziging op: 17-04-2005