Uitcirkels - Aangeschreven cirkels van een driehoek

Overzicht

Inleiding
Eigenschappen
oa. van straal en raaklijnstukken
Mittenpunkt
Meer eigenschappen
waaronder Punt van Nagel, Orthocentrisch systeem
Machtlijnen, homothetie
Clawson-punt
Apollonius-punt
Download

Zie ook de pagina "Incirkel"

1. Inleiding
De bissectrice van een hoek is de verzameling van de punten met gelijke afstand tot de benen van die hoek (zie de pagina "Incirkel").
Dit geldt dus eveneens voor de bissectrices van de buitenhoeken (buitenbissectrices).
Via deze eigenschap vinden we:

Stelling 1
De buitenbissectrices van twee hoeken van een driehoek en de binnenbissectrice van de derde hoek zijn concurrent.
Het gemeenschappelijk punt heet uitcentrum van de driehoek.

Een uitcentrum is het middelpunt van een aangeschreven cirkel, hier uitcirkel genoemd. Een uitcirkel raakt aan een zijde en aan de verlengden van de beide andere zijden van een driehoek (zie de figuur hiernaast).

Definitie
De uitcentra van een driehoek vormen een driehoek die we de uitcentrum-driehoek noemen (Eng: excentral triangle).

In de fguur hiernaast is UaUbUc de uitcentrum-driehoek van driehoek ABC.

Klik hier voor een CabriJavapplet met uitcentrum-driehoek en aancirkels.

2. Eigenschappen

Stelling 2
[1]
Voor de stralen r_a, r_b, r_c van de uitcirkels geldt met 2s = a + b + c en O is de oppervlakte van driehoek ABC:
r_a = O / (s - a), enz.
[2]
De raaklijnstukken uit A, B en C aan de uitcirkel aan de zijde a zijn opvolgend gelijk aan:
s, s - c en s - b.

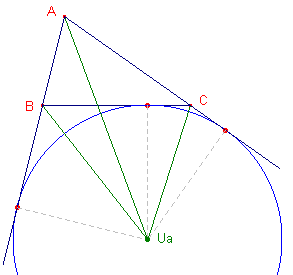
Bewijs: [1], zie nevenstaande figuur.

Opp(ACUa) = ½ r_a · b ......(1)
Opp(ABUa) = ½ r_a · c ......(2)
Opp(BCUa) = ½ r_a · a ......(3)
(1) + (2) - (3) geeft
Opp(ABC) = O = ½ r_a · (b + c - a) = r_a · (s - a)
waaruit het gestelde volgt. ¨

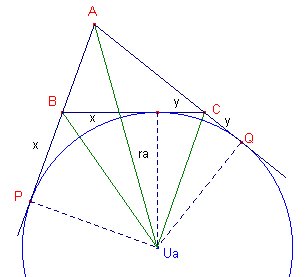
[2], zie bovenstaande figuur.
AP = AQ (raaklijnstukken zijn gelijk)
AP + AQ = c + x + b + y = a + b + c = 2s (immers x + y = a), zodat
AP = AQ = s
x + c = s, waaruit x = BP = s - c
y + b = s, waaruit y = CQ = s - b ¨

Opmerking
De raaklijnstukken uit A, B, C aan de uitcirkel aan de zijde b zijn opvolgend gelijk aan: s - c, s, s - a.
De raaklijnstukken uit A, B, C aan de uitcirkel aan de zijde c zijn opvolgend gelijk aan: s - b, s - a, s.
Zie voor een toepassing Stelling 10.
[einde Opmerking]

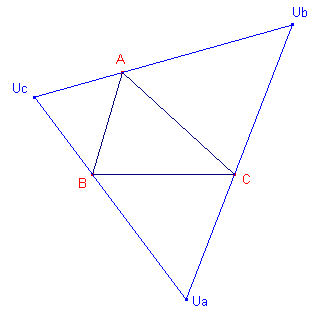
Stelling 3
De bissectrices van de hoeken van driehoek ABC zijn de hoogtelijnen van de uitcentrum-driehoek.

Bewijs:

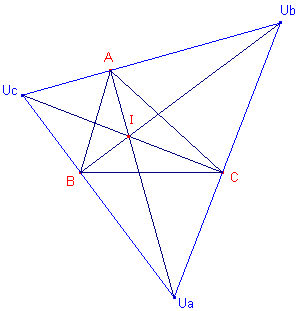UbUc is buitenbissectrice van hoek A. AUa is binnenbissectrice van hoek A. De binnenbissectrice van een hoek staat loodrecht op de buitenbissectrice van die hoek (bissectrices van twee nevenhoeken).
Waaruit het gestelde volgt. ¨

Opmerking
De uitcentrum-driehoek is altijd scherphoekig.
Immers, B en C in vierhoek BUaCI zijn elk 90º.
Hoek Ua is dan gelijk aan ½(B + C) = 90º - ½A < 90º
[einde Opmerking]

Gevolg van Stelling 3
- Driehoek ABC is voetpuntsdriehoek van driehoek UaUbUc (dus I = Hu).
- De zijden van driehoek ABC zijn dus antiparallel met de overeenkomstige zijden van driehoek UaUbUc (zie de pagina "Isogonale verwantschap").
[einde Gevolg]

Klik hier voor een CabriJavapplet als illustratie van het bovenstaande.

We kunnen eea. samenvatten in de volgende stelling:

Stelling 4
Het hoogtepunt en de hoekpunten van een driehoek zijn het incentrum en de uitcentra van de voetpuntsdriehoek van die driehoek.

3. Mittenpunkt
Op de pagina "Isogonale verwantschap" vinden we als Stelling 5.3:

Stelling 5
Een symmediaan van een driehoek gaat door het midden van een lijnstuk dat antiparallel is met de overstaande zijde.

Passen we deze eigenschap toe op de uitcentrum-driehoek van driehoek ABC - in de wetenschap, dat de symmedianen van een driehoek concurrent zijn - dan is het symmediaanpunt (punt van Lemmoine) van de uitcentrum-driehoek het zogenoemde Mittenpunkt van driehoek ABC.

We kunnen dit als volgt formuleren:

Stelling 6
De verbindingslijnen van de hoekpunten van de uitcentra van een driehoek en de middens van de "bijbehorende" zijden zijn concurrent in het Mittenpunkt van de driehoek.

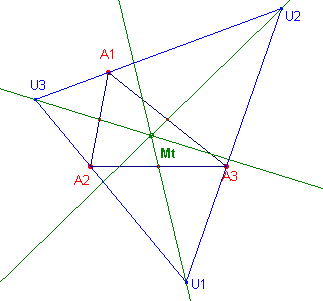Klik hier voor een CabriJavapplet als illustratie van Stelling 6.

Opmerkingen
[1]
Het punt is voor het eerst bestudeerd door Von Nagel (Christian Heinrich von Nagel, 1803-1882, Duitsland) in 1836, en wordt Mittenpunkt genoemd in het boek:
PETER BAPTIST: Die Entwicklung der Neueren Dreiecksgeometrie,Wissenschaftsverlag, Mannheim, 1992 (p. 72).

[2]
Het Mittenpunt wordt in CLARK KIMBERLING: Triangle Centers en Central Triangles (1998, Winnipeg, Canada) aangegeven met X9.
- Zie ook KIMBERLING: "Encyclopedia of Triangle Centers - ETC (website).
- Zie ook Mittenpunkt (X9) op deze website.

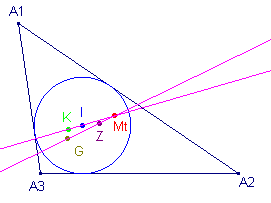In dit boek wordt ook vermeld, dat Mt (X9) het snijpunt is van de lijnen
- KI (opvolgend Lemoine-punt, X6, en incentrum, X1) en
- GZ (opvolgend Gergonne-punt, X7, en zwaartepunt, X2 )
(X-codering volgens Kimberling).

Klik hier voor een CabriJavapplet van deze eigenschap.

[3]
Zie ook de pagina "Barycentrische coördinaten"

[einde Opmerkingen]

4. Meer eigenschappen

Lemma
De loodlijn uit een hoekpunt op de zijde van de voetpuntsdriehoek die antiparallel is met de tegenoverliggende zijde, is het spiegelbeeld van de hoogtelijn uit dat hoekpunt in de bissectrice uit dat hoekpunt (maw. er is sprake van isogonale verwantschap).

Bewijs:

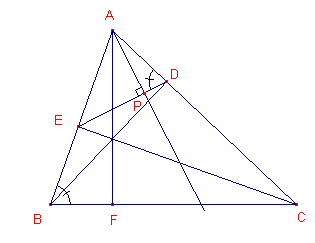Zie nevenstaande figuur.
In driehoek APD is A = 90º - D = 90º - B.
In driehoek BFA is A = 90º - B.
Waaruit het gestelde onmiddellijk volgt. ¨

Gevolgen
[1]
De loodlijnen uit de hoekpunten op de zijden van de voetpuntsdriehoek zijn concurrent.
[2]
Bekend is dat het hoogtepunt en het middelpunt van de omcirkel isogonaal verwant zijn (zie Stelling 3b op de pagina "Isogonale verwantschap").
De bedoelde loodlijnen gaan dus door het omcentrum van driehoek ABC.

[einde Gevolgen]

Stelling 7
De loodlijnen uit de uitcentra U1, U2, U3 op de "bijbehorende" zijde van driehoek A1A2A3 zijn concurrent.

Opmerking
Het gemeenschappelijk punt, O_u, is het omcentrum van driehoek U1U2U3.
[einde Opmerking]

Bewijs:
De loodlijnen op de zijden van A1A2A3 zijn loodlijnen op de antiparallellen van de zijden van driehoek U1U2U3 (zie het gevolg van Stelling 3).
Volgens bovenstaand lemma zijn deze lijnen concurrent in het middelpunt van de omcirkel van driehoek U1U2U3. ¨

Punt van Nagel

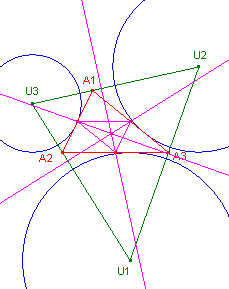
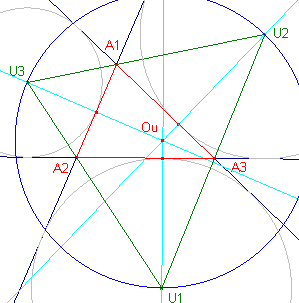
De raakpunten van de uitcirkels aan de zijden zijn in nevenstaande tekening G1, G2, G3.
De lijnen A_iG_i zijn concurrent in het punt N, het Nagel-punt van driehoek A1A2A3.

Zie hiervoor ook de pagina Transversalen, paragraaf 4.6.

Opmerkingen
[1]
Op de pagina "Collineaties" wordt bewezen, dat het incentrum, het zwaartepunt en het Nagel-punt collineair zijn.
[2]
Zie ook de pagina "Barycentrische coõrdinaten"
[einde Opmerking]

Orthocentrisch systeem

Definitie
Een orthocentrisch systeem is een verzameling van vier punten, waarvan een punt hoogtepunt is van de driehoek gevormd door de drie andere punten.

We kunnen op basis van deze definitie algemeen bewijzen:

Stelling 8
In een orthocentrisch systeem is elk punt hoogtepunt van de driehoek gevormd door de andere drie punten.

Bewijs:

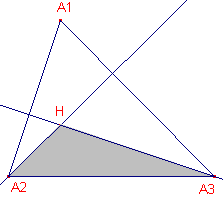Zij H het hoogtepunt van driehoek A1A2A3.
A1,A2,A3, H vormen dus een orthocentrisch systeem.
Nu zijn A2A1 en A3A1 hoogtelijnen van driehoek A2A3H.
A1 is dus hoogtepunt van driehoek A2A3H.
Analoog voor de andere mogelijke driehoeken. ¨

Gevolg
Een orthocentrisch systeem bepaalt één negenpuntcirkel.

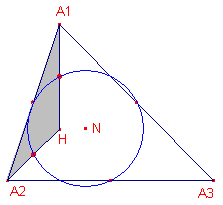Bewijs: Zij namelijk N het middelpunt van de negenpuntscirkel van A1A2A3.
Cirkel N gaat door de middens van A1A2 en van HA1 en HA2.
N is dus eveneens negenpuntcirkel van driehoek HA1A2.
Enzovoorts. ¨

Stelling 9a
De vier omcirkels van een orthocentrisch systeem hebben gelijke straal.

Bewijs:

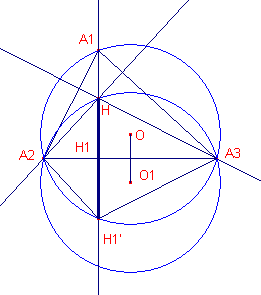We bekijken de omcirkel van A1A2A3 en van A2A3H.
Volgens een bekende eigenschap is nu HH1 = H1H1'.
De driehoeken A2A3H en A2A3H1' zijn daardoor congruent. De stralen van hun omcirkels zijn dus gelijk.
Waaruit het gestelde, analoog voor de andere mogelijkheden, volgt. ¨

Opmerking
De middelpunten van de omcirkels zijn elkaars spiegelbeeld in de zijden van A1A2A3.
[einde Opmerking]

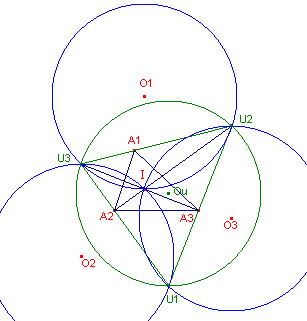Gevolgen
[1]

Stelling 9b
- U1, U2, U3, I vormen een orthocentrisch systeem.
- De omcirkels van U1U2U3, U1U2I, U2U3I, U3U1I hebben gelijke straal

Bewijs: Zie Stelling 3 en Stelling 9a. ¨

[2]

Stelling 9c
- De stralen van de omcirkels van A1A2A3 en U1U2U3 verhouden zich als 1 : 2.
- De punten I, O, Ou zijn collineair, waarbij O het midden is van IOu.

Bewijs:
De omcirkel van A1A2A3 is de negenpuntcirkel van U1U2U3 (zie Stelling 3). Het punt I (hoogtepunt van U1U2U3) is centrum van vermenigvuldiging met ½, waardoor de omcirkel van U1U2U3 overgaat in de omcirkel van A1A2A3. ¨

Opmerking
Deze eigenschap is voor het eerst vermeld door M.J. Mention in 1849, en opgenomen in het tijdschrift Nouvelles Annales de Mathématiques (1850, p.324).
[einde Opmerking]

5. Machtlijnen, homothetie

Stelling 10
De machtlijnen van de uitcirkels van een driehoek zijn de bissectrices van de centrumdriehoek van die driehoek.

Opmerking
De centrumdriehoek is de driehoek met de middens van de zijden als hoekpunten.
[einde Opmerking]

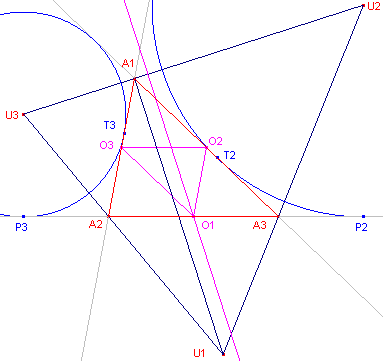Bewijs:
O1O2O3 is de centrumdriehoek van A1A2A3.
Uit Stelling 2.2 volgt, dat A2P3 = A3P2 (beide gelijk aan s - a).
Het punt O1 (het midden van A2A3) heeft dus gelijke machten ten opzichte van de uitcirkels (met middelpunt) U2 en U3; immers O1P3 = O1P2.
O1 ligt dus op de machtlijn van de uitcirkels U2 en U3.
De machtlijn staat loodrecht op U2U3, en is dus evenwijdig met A1U1 (zie Stelling 3).
A1U1 is bissectrice van hoek A1, terwijl de benen van hoek O1 (in driehoek O1O2O3) evenwijdig zijn met de benen van hoek A1.
De machtlijn van de uitcirkels U2 en U3 is dus bissectrice van hoek O1. ¨

Opmerking
Het gevolg hiervan is:

Het machtpunt van de drie uitcirkels is het incentrum van de centrumdriehoek.

[einde Opmerking]

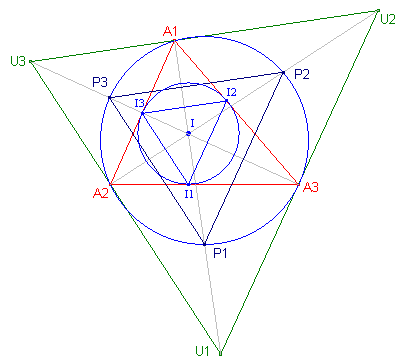In de figuur hiernaast zijn:
- P1, P2, P3 snijpunten van de omcirkel van driehoek A met de binnenbissectrices
- I1, I2, I3 raakpunten van de incrkel met driehoek A
Nu geldt:

Stelling 11
[1]
De driehoeken U en P zijn homothetisch (gelijkstandig) met centrum I en verhouding 2 : 1.
[2]
De driehoeken I en P zijn homothetisch.

Bewijs:
[1]
De lijnen A_iU_i zijn de hoogtelijnen van driehoek U, waarvan I hoogtepunt is (zie Stelling 3).
De omcirkel van driehoek A is de negenpuntcirkel van driehoek U. De punten P_i zijn dus de hoekpunten van de Euler-driehoek van driehoekU.
Van de Euler-driehoek van een driehoek is bekend dat deze homothetisch is met die driehoek (zie Stelling 2 op de pagina "Euler-driehoek"). Het centrum is het hoogtepunt (in dit geval het punt I).

Uit het feit dat P_iP_j middenparallell is van U_iU_j volgt nu direct dat de verhouding 2 : 1 is. ¨

[2]
I I2 _|_ A1A3 en ook I I3 _|_ A1A2. I I2A1I3 is dus een koordenvierhoek, waarbij ook I I2 = I I3. De koordenvierhoek is dus een vlieger.
Zodat
IA1 _|_ I2I3 ......(1)
Maar ook IA1 _|_ U2U3 (hoogtelijn en zijde) ......(2)
Uit (1) en (2) volgt dus, mutatis mutandi, dat de zijden van driehoek I evenwijdig zijn met de overeenkomstige zijden van driehoek U die op hun beurt weer evenwijdig zijn met de overeenkomstige zijden van driehoek P (zie Stelling 11.1).
Hetgeen betekent, dat de driehoek I en P homothetisch zijn. ¨

Opmerking
Driehoek I is de zogenoemde Gergonne-driehoek van driehoek A.
[einde Opmerking]

Stelling 12
[1]
De verbindingskoorden van de raakpunten van de incirkel van een driehoek zijn evenwijdig met de overeenkomstige buitenbissectrices.
[2]
De koorden naar de raakpunten van een uitcrkel zijn evenwijdig met de buitenbissectrice van de overstaande hoek en de binnenbissectrices van de beide andere hoeken.

Bewijs:
[1] Zie Stelling 11 en de daarbij behorende figuur. Bijvoorbeeld: I2I3 // U2U3. ¨

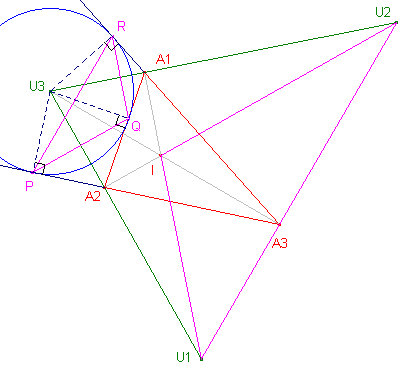[2]
Zie nevenstaande figuur, waarin de bedoelde koordes PR, PQ en QR zijn.
Aan te tonen is: PR // U1U2, PQ // A2U2, QR // A1U1.

Uit het feit, dat A1RU3Q een vlieger is, volgt, dat QR _|_ U2U3.
Maar ook A1U1 _|_ U2U3, zodat
QR // A1U1
Op dezelfde manier bewijzen we dat PQ // A2U2.
Verder is U3P = U3R en A3P = A3R, waaruit volgt, dat PA3RU3 een vlieger is.
PR staat dus, evenals U1U2, loodrecht op A3U3.
Waaruit volgt dat PR // U1U2. ¨

Gevolg
De voetpuntsdriehoek van het incentrum of van het uitcentrum van een driehoek is gelijkvormig (en homothetisch) met de driehoek die de andere punten als hoekpunten heeft.

Voorbeeld: in de figuur hiernaast is PQR ~ U2IU1.

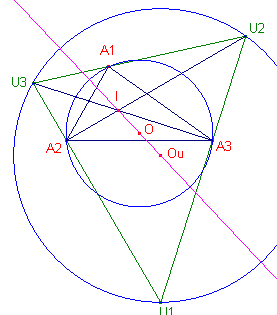
Stelling 13
De driehoeken U en I hebben dezelfde Euler-lijn (te weten de lijn OI).

Bewijs:

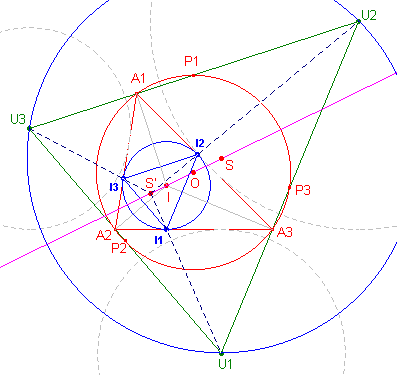De lijn A1I is binnenbissectrice van driehoek A.
De lijn U2U3 is buitenbissectrice van driehoek A.
Dus A1I _|_ U2U3.
De lijn A1I is dus hoogtelijn van driehoek U.
I is dus het hoogtepunt van driehoek U.
O is het middelpunt van de omcirkel van driehoek A, maar driehoek A is ook voetpuntsdriehoek van van driehoek U.
O is dus het negenpuntsmiddelpunt van driehoek U (de middens van de zijden van driehoek U zijn P1, P2, P3).
OI is dus de Euler-lijn van driehoek U.

Gevolg: het punt S, het middelpunt van de omcirkel van driehoek U, ligt dus op OI.

Uit Stelling 11.2 volgt de gelijkvormigheid van I en U.
Wegens I2I3 // U2U3, etc. volgt hieruit gelijkstandigheid (homothetie).
De factor (van I naar U) is gelijk aan 2R/r, immers de omcirkel van driehoek A (met straal R) is de negenpuntscirkel van driehoek U.
I is middelpunt van de omcirkel van driehoek I.
Omdat I en S op OI liggen, ligt het centrum S' van de homologie dus eveneens op OI.

Het hoogtepunt van driehoek U, zijnde I, ligt op de lijn OI. Het hoogtepunt van driehoek I ligt dus, vanwege de homothetie, eveneens op de lijn OI.
OI is dus eveneens Euler-lijn van driehoek I. ¨

6. Clawson-punt

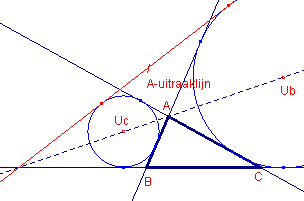De zijden van driehoek ABC zijn (in- en uitwendige) raaklijnen aan de uitcirkels. Elk tweetal uitcirkels (bijvoorbeeld de B-uitcirkel en de C-uitcirkel) heeft echter 4 raaklijnen. Die vierde raaklijn is geen zijde van driehoek ABC. Deze raaklijn zou kunnen worden naamgegeven met A-uitraaklijn (Eng. A-extangent).

Definitie
De A-, B-, C-uitraaklijnen van een driehoek vormen een driehoek die de uitraaklijnen-driehoek (Eng. extangents triangle) van driehoek ABC heet.

Opmerking
De uitraaklijnen-driehoek is dus op te vatten als de omhullende driehoek van de uitcirkels van een driehoek.
[einde Opmerking]

Stelling 14
De uitraaklijnen-driehoek en de hoogtepuntsdriehoek zijn gelijkstandig (homothetisch).
Het centrum van de homothetie heet Clawson-punt.

Bewijs:

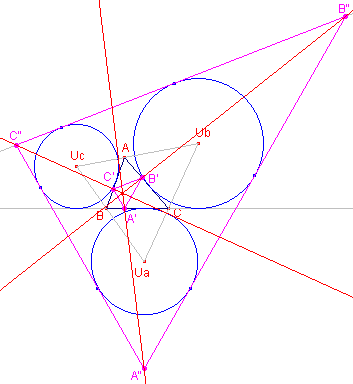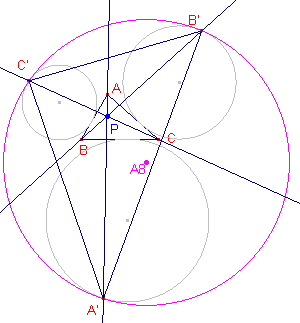
De zijde B"C" van de uitraaklijnen-driehoek is het spiegelbeeld van de lijn BC in de lijn door Uben Uc (centra van uitcirkels).
Volgens het Gevolg van Stelling 3 is UbUc antiparallel met BC.
Is nu A'B'C' de hoogtepuntsdriehoek, dan geldt:
B'C' en B"C" zijn evenwijdig, immers ook B'C' is antiparallel met BC..
Evenzo is C"A" // C'A' en A"B" // A'B'.
De driehoeken A'B'C' en A"B"C" zijn dus gelijkstandig.
De lijnen A'A", B'B", C'C" zijn dus concurrent. ¨

Opmerking
Zie ook de pagina "Bijzondere punten..."; Kimberling's TCCT: X19.
[einde Opmerking]

7. Apollonius-punt
De omhullende cirkel van de drie uitcirkels van een driehoek kan worden gevonden als deel van de oplossing van het Raakprobleem van Apollonius (bij geval A003; namelijk de cirkel waaraan de drie gegeven cirkels inwendig raken).
Er blijkt dan:

Stelling 15
De driehoek met als hoekpunten de gemeenschappelijke raakpunten van de "omhullende" cirkel van de uitcirkels van een driehoek is perspectief met die driehoek.
De perspector wordt het Apollonius-punt van de oorspronkelijke driehoek genoemd.

Opmerking
Zie ook de pagina "Bijzondere punten..."; Kimberling's TCCT: X181.
[einde Opmerking]

8. Download
De figuren die in de CabriJavapplets zijn gebruikt kunnen in één bestand via deze website worden gedownload. In dit bestand is ook de Cabri-macro UitcentrumDriehoek.MAC opgenomen, alsmede enkele andere figuren die samenhangen met de tekst op deze webpagina.
Klik hier om het downloadproces te starten (ZIP-bestand; ca. 12kB).

[uitcirkels.htm] laatste wijziging op: 11-04-05