Euler-driehoek

Definitie
De Euler-driehoek van een driehoek heeft als hoekpunten de middens van de "bovenste loodlijnstukken" van die driehoek.

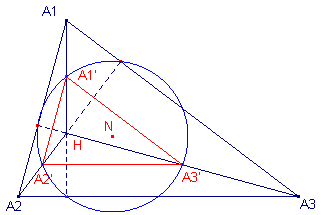De Euler-driehoek hangt nauw samen met de negenpuntcirkel van een driehoek, immers de negenpuntcirkel gaat door de middens van de "bovenste loodlijnstukken" (dit zijn de stukken van de loodlijnen tussen een hoekpunt en het hoogtepunt. Zodat geldt:

Stelling 1
De negenpuntcirkel is de omcirkel van de Euler-driehoek.

en ook (zie bovenstaande figuur):

Stelling 2
A1A2A3 is homothetisch (gelijkstandig) met A1'A2'A3' (Euler-driehoek), waarbij H het centrum is en de verhouding gelijk is aan 2 : 1.

Op basis van een vermenigvuldiging met factor -½ (tov. het zwaartepunt van A1A2A3) vinden we ook eenvoudig;

Stelling 3
De Euler-driehoek is congruent en homothetisch met de centrumdriehoek.
Het centrum van de homothetie is het middelpunt van de negenpuntcirkel

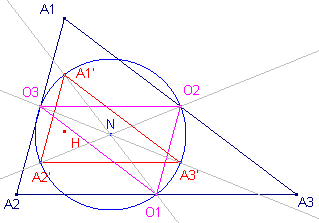In de figuur hiernaast is O1O2O3 de centrumdriehoek.

Opmerking
De negenpuntcirkel (middelpunt N) is eveneens omcirkel van de centrumdriehoek.
[einde Opmerking]

Verder is duidelijk dat

Stelling 4
De Euler-driehoek is perspectief met de voetpuntsdriehoek (van het hoogtepunt).
Het perspectiefcentrum is het punt H.

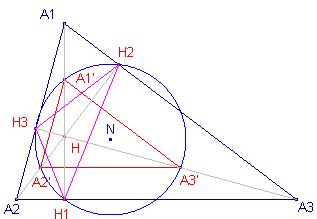In de figuur hiernaast is H1H2H3 de voetpuntsdriehoek van het hoogtepunt H.

Opmerking
De negenpuntcirkel (middelpunt N) is eveneens omcirkel van de voetpuntsdriehoek.
[einde Opmerking]

Alle genoemde driehoeken staan hieronder in dezelfde figuur.

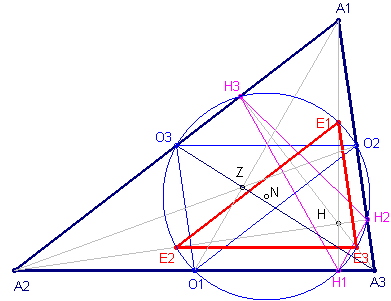E1E2E3 is de Euler-driehoek
O1O2O3 is de centrumdriehoek
H1H2H3 is de voetpuntsdriehoek.

H is het hoogtepunt (X4)
Z is het zwaartepunt (X2)
N is het middelpunt van de negenpuntcirkel (X5)

De naamgeving van de punten met X (tussen haakjes hierboven) is conform Kimberling's TCCT (*).

Referentie
(*) CLARK KIMBERLING: Triangle Centers and Central Triangles (1998, Winnipeg, Canada)
Zie ook ETC (Encyclopedia of Triangle Centers)

[eulerdrie.htm] laatste wijziging op: 15-04-03