Het raakprobleem van Apollonius

Overzicht ][ Inversie | Geschiedenis | Meetkunde

Overzicht

Inleiding
Overzicht deelproblemen
Algemene oplossing

Zie ook de pagina "Raakprobleem(2)" waarop enkele constructies worden behandeld op basis van standaard bewerkingen, zoals vermenigvuldiging en machten.
Bij de deelproblemen (zie paragraaf 2) wordt verwezen naar deze standaard oplossingen.

1. Inleiding
In twee verloren gegane boeken, getiteld De Tactionibus (Over aanrakingen), beschrijft Apollonius van Perga (~262 - ~190 vC) een beroemd geworden raakprobleem :

Gegeven drie dingen, waarvan elk een punt, een lijn of een cirkel kan zijn.
Bepaal een cirkel die door elk der gegeven punten gaat en die de gegeven lijnen of cirkels raakt.
Zie figuur 3.

Voor een reconstructie van de inhoud van de boeken van Apollonius zie Th. Heath, History of Greek Mathematics I, pg 182 ev.
Ook eerdere wiskundigen hebben zich uiteraard met het raakprobleem bezig gehouden; oa.
- Francois Viete, ook wel Vieta (1540-1603, Frankrijk), heeft getracht het werk van Apollonius te reconstrueren (1600).
- C.F. Gauss, Complete Works, vol. IV, pg 399
- J. Gergonne, Annales de Mathématiques, vol. IV (De oplossing van het probleem zoals Gergonne dat deed, wordt, met weglating van de vele details, weergegeven in paragraaf 3)
- J. Petersen, Methoden und Theorien

2. Overzicht deelproblemen
We kunnen het probleem opsplitsen in de volgende gevallen:

	punten	lijnen	cirkels	code		standaard

I.	3	-	-	A300
II.	2	1	-	A210	I	S210
III.	2	-	1	A201	I	S201
IV.	1	2	-	A120	I	S120
V.	1	-	2	A102	I	S102
VI.	1	1	1	A111	I	S111
VII.	-	3	-	A030
VIII.	-	2	1	A021
IX.	-	1	2	A012
X.	-	-	3	A003

Alle gevallen kunnen met, zij het soms niet eenvoudige, elementaire constructiemethoden worden opgelost (zie daarvoor ook de pagina "Raakprobleem(2)"), maar voor de meeste gevallen ligt het gebruik van inversie toch zeker voor de hand ligt (deze zijn hierboven met een I aangegeven).
Overigens kunnen we alle gevallen tot één terug brengen door punten op te vatten als cirkels met een straal gelijk aan 0 en rechte lijnen als cirkels met een oneindig grote straal (in beide gevallen spraken we dan van ontaarde cirkels).

Dat de gevallen waarbij geen punt betrokken is, niet direct met het gebruik van inversie kunnen worden opgelost, ligt eigenlijk voor de hand. Immers, bij inversie worden lijnen meestal op cirkels en cirkels op lijnen afgebeeld. Passen we op deze gevallen inversie toe, dan verandert er meestal niet veel aan het probleem.
Soms echter kan een bijzondere ligging en/of het handig kiezen van de inversiecirkel, evenwel inversie toelaten (zie A003).

I - A300 - drie punten
Eenvoudiger kan het niet.
De gevraagde cirkel is de omgeschreven cirkel van de driehoek met die punten als hoekpunten.
Als de drie punten collineair zijn, dan valt de gevraagde (ontaarde) cirkel samen met de drager van de punten.

II - A210 - twee punten P en Q en een lijn l
Zie figuur A210.

figuur A210

Zij R het voetpunt van de loodlijn uit P op l.
We kiezen nu de cirkel met middelpunt P en straal PR als inversiecirkel.

Door deze inversie gaat de lijn l over in een cirkel l' en het punt Q in een punt Q'.
De gevraagde cirkels kunnen dus gevonden worden als de inversen van de raaklijnen uit Q' aan de cirkel l' (de inverse van l).

Opmerking
Klik hier voor de standaard-oplossing (S210)
[einde Opmerking]

III - A201 - twee punten P en Q en een cirkel K
Zie figuur A201a, waarin we de beide punten buiten de cirkel K plaatsen.

figuur A201
a

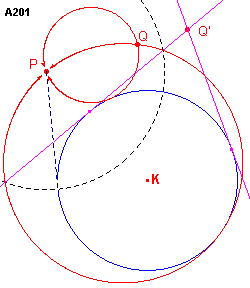We kiezen het punt P als centrum van inversie en de macht van P tov. de cirkel K als inversiemacht.

Door deze inversie gaat de cirkel K over in zichzelf en het punt Q in een punt Q'.
De gevraagde cirkels kunnen dus gevonden worden als inversen van de raaklijnen uit Q' aan de cirkel K.

Ook indien beide punten binnen K liggen, kunnen we het probleem oplossen. De macht van P is hier negatief, zodat we eerst een inversie toepassen met de cirkel K zelf als inversiecirkel.
Door deze inversie worden de punten P, Q afgebeeld op de punten P', Q' die beide buiten de cirkel K liggen.
Hiermee is het probleem dus terug gebracht tot het zojuist opgeloste. Zie verder figuur A201b.

figuur A201
b

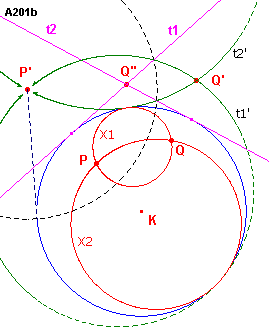De punten P', Q' zijn de beelden van P, Q bij inversie ten opzichte van cirkel K.
We kiezen nu P' als centrum van de inversie, waarvan de inversiemacht gelijk is aan de macht van P' ten opzichte van K.
Bij deze laatste inversie gaat K over in zichzelf. Q' wordt hierbij afgebeeld op het punt Q".
We gaan nu op dezelfde manier te werk als beschreven bij A201a.
t₁, t₂ zijn de raaklijnen uit Q" aan K. De beide inversies geven dan opvolgend de beelden t₁', t₂' (cirkels) en X₁, X₂ (de gevraagde cirkels).

Opmerking
Klik hier voor de standaard-oplossing (S201)
[einde Opmerking]

IV - A120 - een punt P en twee lijnen l en m
Zie figuur A120/

figuur A120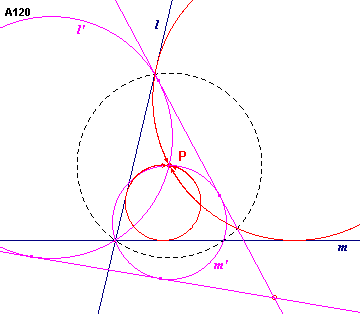

We kiezen het punt P als middelpunt van de inversiecirkel, die we laten gaan door het snijpunt van de lijnen l en m.

Door deze inversie gaan de lijnen l, m over in twee (elkaar snijdende cirkels l' en m'.
De gevraagde cirkels kunnen dus gevonden worden als de inversen van de (beide) gemeenschappelijke raaklijnen van l' en m'.

Opmerking
Klik hier voor de standaard-oplossing (S120)
[einde Opmerking]

V - A102 - een punt P en twee cirkels K₁ en K₂
Zie figuur A102.

figuur A102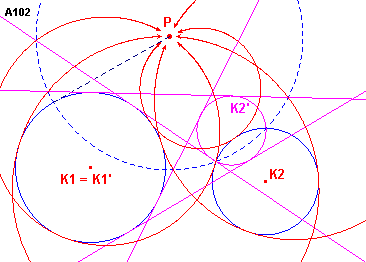

We kiezen het punt P als centrum van de inversie met als inversiemacht de macht van P tov. de cirkel K₁.

Door deze inversie gaat de cirkel K₁ over inzelf en wordt de cirkel K₂ afgebeeld op een cirkel K₂'.
De gevraagde cirkels kunnen dus gevonden worden als inversen van de (vier) gemeenschappelijke raaklijnen aan K₁' en K₂'.

Opmerking
Klik hier voor de standaard-oplossing (S102)
[einde Opmerking]

VI - A111 - een punt P, een lijn l en een cirkel K
Zie figuur A111.

figuur A111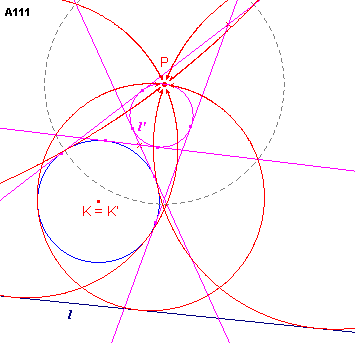

We kiezen het punt P als inversiecentrum en de macht van P ten opzichte van de cirkel K als inversiemacht.

Door deze inversie gaat de cirkel K over in zichzelf, terwijl de lijn l wordt afgebeeld op een cirkel l'.
De gevraagde cirkels kunnen dus gevonden worden als inversen van de (maximaal vier) gemeenschappelijke raaklijnen van de cirkels K' en l'.

Opmerking
Klik hier voor de standaard-oplossing (S111)
[einde Opmerking]

VII - A030 - drie lijnen
De (maximaal vier) te construeren cirkels zijn de incirkel en de drie uitcirkels van de driehoek die door de drie lijnen wordt ingesloten.

VIII - A021 - twee lijnen l, m en een cirkel K
Zie figuur A021.

figuur A021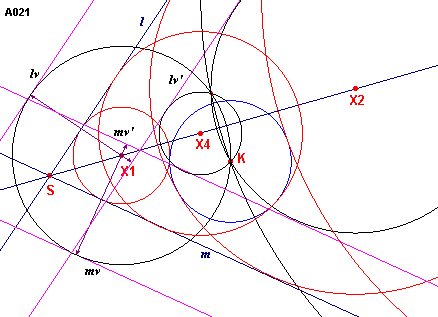

We kunnen dit geval terugbrengen tot geval IV, A120, en wel door de volgende redenering.

Als een cirkel X moet raken aan l en m en aan de cirkel K, dan bestaat er een (met X) concentrische cirkel door het middelpunt van K die raakt aan de lijnen l_v en m_v (de over de straalafstand van K evenwijdig verschoven lijnen l en m).
We dienen dus de cirkels te construeren, die door K gaan, en raken aan de lijnen l_v en m_v.
In de figuur zijn dat de cirkels X₁ en X₃ (van X3 is het middelpunt niet zichtbaar).
Omdat we de translatie in twee richtingen kunnen uitvoeren zijn er mogelijk ook nog twee andere oplossingen (zie de cirkels X₂ en X₄, met lijnen l_v' en m_v').

IX - A012 - een lijn l en twee cirkels K₁ en K₂
Zie figuur A012.

figuur A012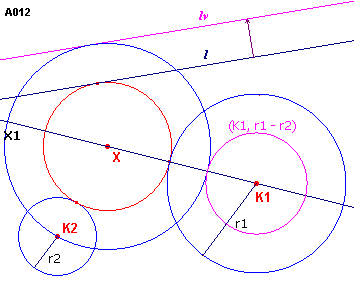

We onderstellen hierbij, dat voor de stralen van r₁ en r₂ van K₁ en K₂ geldt r₁ > r₂.
We kunnen nu de constructie terugbrengen tot geval VI, A111, en wel door de volgende redenering.

Een cirkel X die raakt aan l en aan K₁ en K₂, is concentrisch met een cirkel X₁ die raakt aan l_v (de lijn die evenwijdig aan l verschoven is over de afstand r₂), gaat door K₂ en raakt aan de cirkel (K1, r₁-r₂).
We kunnen ook hier de verplaatsing van l in twee richtingen laten plaats vinden. Voorts is ook raking mogelijk aan de de cirkel (K₁, r₁+r₂).
Het maximaal aantal oplossingen is dus 8.

In figuur A012b zijn 4 van deze 8 mogelijke oplossingen weergegeven.

figuur A012
b

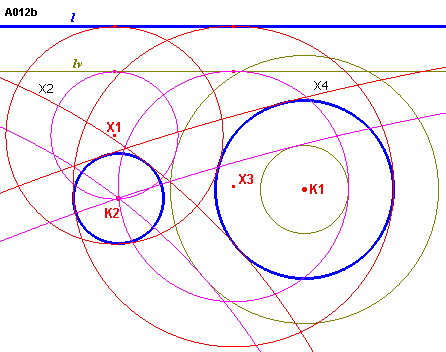Het zijn de 4 cirkels die als basis de raakcirkels hebben aan l_v (de hulpcirkels X_i').
Van deze hulpcirkels X_i' is de straal verminderd met r₂.

X₁' en X₂' raken aan de cirkel (K₁, r₁+r₂)
X₃' en X₄' raken aan de cirkel (K₁, r₁-r₂).

Aanloog kunnen de overige 4 cirkels worden geconstrueerd.
Deze raken aan de lijn l_v'; dit is de lijn die over de afstand r₂ evenwijdig met l verplaatst is in de andere richting.

X - A003 - drie cirkels K₁, K₂en K₃
We lossen dit probleem eerst op in het geval de drie cirkels door één punt M gaan en de centralen niet samenvallen. Zie figuur A003a.

figuur A003
a

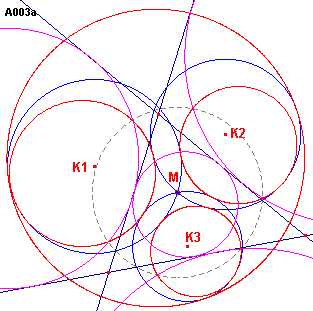Kiezen we M als centrum van een inversie met een inversiecirkel die de drie cirkels snijdt, dan gaan de cirkels K_i over in rechte lijnen, die een driehoek insluiten.
De gevraagde cirkels (vier) zijn dus de beelden van de incirkel en de uitcirkels van die driehoek bij de gebruikte inversie.

Zoals opgemerkt kunnen we soms door een bijzondere ligging het probleem terugbrengen tot een eerder behandeld geval.
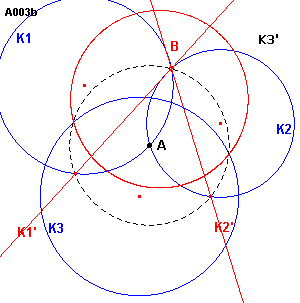
In figuur A003b zien we dat de drie cirkels elkaar twee aan twee snijden.

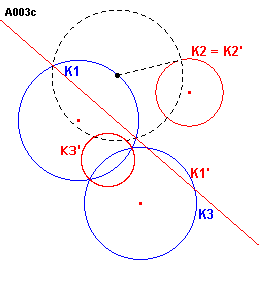
figuur A003 b		figuurA003 c

Snijden K₁ en K₂ elkaar in A en B dan kunnen we A als centrum van inversie en de lengte van AB als inversiemacht nemen.
Hierdoor gaan K₁, K₂ over in de rechte lijnen K₁', K₂', terwijl K₃ overgaat in een nieuwe cirkel K₃'.
Het probleem is hierdoor teruggebracht tot geval VIII, A021, twee lijnen en een cirkel.
Hieraan is evenwel gemakkelijk te zien, dat het algemene geval maximaal 8 oplossingen toelaat.

Indien de cirkels elkaar niet snijden (zie figuur A003c), dan kunnen we reduceren tot geval IX, A012, een lijn en twee cirkels, door het inversiecentrum te plaatsen op (bijvoorbeeld) K₁ en de inversiemacht gelijk te nemen aan de macht van het centrum ten opzichte van (bijvoorbeeld) K₂.
Hierdoor gaar K₁ over in de rechte lijn K₁', K₂ in zichzelf en K₃ in een nieuwe cirkel K₃'.

3. Algemene oplossing van A003
Voor een algemene oplossing van het geval X, A003, kunnen we gebruik maken van elementaire eigenschappen van homothetieën (dit zijn vermenigvuldigingen tov. een punt) en van de hoofdstelling van de pooltheorie (die evenwel samenhangt met de theorie der inversies).

De oplossing van het raakprobleem valt in vier delen uiteen:

Raking van drie cirkels en de gelijkvormigheidspunten van twee ervan
Verband met machten
Verband met de pooltheorie
De constructie van de raakcirkels

3.1. Raking van drie cirkels en de gelijkvormigheidspunten van twee ervan
We gaan uit van twee cirkels A en B, waaraan een derde cirkel X raakt (opvolgend in de punten P en Q); zie figuur 1.

figuur 1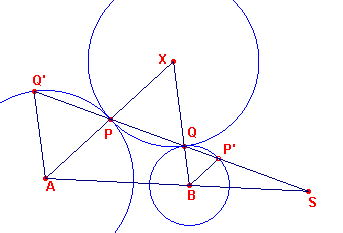

De lijn PQ snijdt AB in het punt S en de cirkels A en B ook nog in Q' en P'.
Duidelijk is, dat de driehoeken APQ', XPQ, BP'Q gelijkvormig zijn (gelijkbenige driehoeken).
Het punt S is dus het (uitwendig) gelijkvormigheidspunt van de cirkels A en B.
Zodat:
SP' : SP = SQ : SQ'
De producten SP · SQ en SP' · SQ' zijn dus aan elkaar gelijk. Stel ze beide gelijk aan w.
Nu is
w² = (SP' · SQ) · (SP · SQ')

en dit is het product van de machten van S ten opzichte van de cirkels A en B. w² = I is dus constant. Geldt ook
SP · SQ = ÖI
eveneens constant. Deze waarde is dus onafhankelijk van de ligging van de cirkel X (en van de raakpunten)..
We komen zo tot de volgende in paragraaf 3.2 te gebruiken

Raakcirkel-stelling
Het (uit- of inwendig) gelijkvormigheidspunt van twee cirkels heeft dezelfde macht ten opzichte van alle cirkels die aan beide cirkels raken.
De lijn die de raakpunten verbindt, gaat steeds door het betreffende gelijkvormigheidspunt.

3.2. Verband met machten
Gaan we uit van het paar cirkels X₁ en X₂ dat opvolgend raakt aan de cirkels A, B, C.
Raken de cirkels X₁, X₂ aan de drie cirkels in opvolgend P₁ en P₂, Q₁ en Q₂, R₁ en R₂, dan gaan de koorden P₁P₂, Q₁Q₂, R₁R₂ door het machtpunt van A,B,C. Dit volgt voor het paar X1, X2 en telkens cirkel A, B of C daaraan rakend uit de Raakcirkel-stelling.

Drie van de zes gelijkvormigheidspunten van A,B,C liggen telkens op een rechte lijn, een gelijkvormigheidsas van de drie cirkels (dit is de Stelling van d'Alembert).
Noteren we zo'n gelijkvormigheidspunt van A,B met S(AB), dan geldt eveneens volgens de Raakcirkel-stelling:
   S(AB) heeft gelijke machten ten opzichte van X₁ en X₂
   S(BC) heeft gelijke machten ten opzichte van X₁ en X₂
   S(CA) heeft gelijke machten ten opzichte van X₁ en X₂
De gelijkvormigheidsas waarop deze drie punten, liggen is dus de machtlijn van X₁ en X₂.

3.3. Verband met de pooltheorie
Zie hiervoor figuur 2.

figuur 2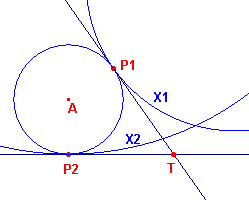

Zij T het snijpunt van de (gemeenschappelijke) raaklijnen in P₁ en P₂ aan cirkel A (en aan X₁ opvolgend X₂).
Het punt T ligt ook op de machtlijn van X₁ en X₂, immers T heeft gelijke machten ten opzichte van cirkel A.
Maar T is eveneens de pool van de lijn P₁P₂ ten opzichte van de cirkel A.

Analoog kan worden geredeneerd voor de raakpunten op de cirkels B en C.

3.4. De constructie van de raakcirkels
Op basis van hetgeen gevonden is in de paragraaf 3.1, paragraaf 3.2 en paragraaf 3.3 kunnen we de constructie dus als volgt beschrijven:

Construeer het machtpunt O van de drie cirkels (in figuur 3 zijn deze aangegeven van K₁, K₂, K₃).
Construeer de gelijkvormigheidsassen van de cirkels (4 in getal).
Bepaal bij elke cirkel de pool van elk van deze vier assen.
Verbind de pool met O en bepaal de snijpunten met de cirkel(s).
Deze snijpunten zijn dus de raakpunten van de gezochte cirkel.

Het resultaat van het bovenstaande staat in figuur 3.

figuur 3

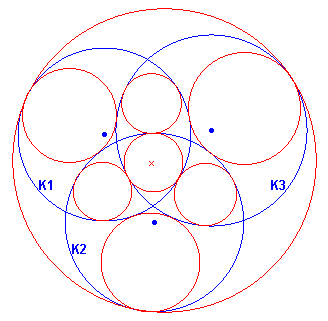Opmerkingen
[1]
De behandeling van de oplossing van het Raakprobleem van Apollonius in paragraaf 3 komt overeen met de wijze waarop het probleem is opgelost door Gergonne.
[2]
Indien de drie cirkels in geval A003 elkaar twee aan twee raken hebben we de Cirkelstelling van Descartes. Er zijn dan twee oplossingen van het raakprobleem. Deze oplossingen worden Soddy-cirkels (naar Sir Frederick Soddy, 1877-1956, Engeland) genoemd.
Zie hiervoor de pagina "Soddy-cirkels".
[3] Zie ook de pagina "Raakprobleem(2)" waarop enkele constructies worden behandeld op basis van standaard bewerkingen, zoals vermenigvuldiging en machten.

[einde Opmerkingen]

[raakprob.htm] laatste wijziging op: 27-12-2004