Soddy-cirkels

Overzicht  ][  Apollonius  |  Heron's formule   |  Inversie  |  Meetkunde

Zie ook het Cabri-werkblad "Inversie".

Overzicht terug

  1. Inleiding
  2. Existentie van de Soddy-cirkels
         2.1. De middelpunten zijn niet-collineair
         2.2. De middelpunten zijn collineair
  3. Cirkelstelling van Descartes
  4. Sir Frederick Soddy
  5. Isoperimetrisch punt
  6. Tenslotte
       wo. Afstand tussen Soddy-cirkels

1. Inleiding terug
Het raakrobleem van Apollonius (zie de betreffende pagina) houdt in het vinden van alle cirkels (eventueel tot rechte lijnen ontaard) die aan drie gegeven cirkels (ook eventueel ontaarde) raken.

Een bijzonder geval van dit probleem wordt in onderstaande paragrafen behandeld, namelijk als de drie gegeven cirkels elkaar twee aan twee raken (zie figuur 1).

figuur 1 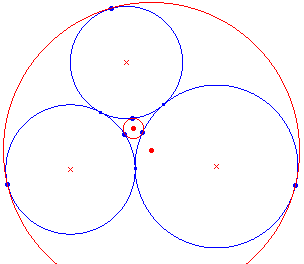soddy1 Deze configuratie komt overeen met het Porisma van Steiner voor n = 3.
Klik hier voor de betreffende pagina.

Opmerking
Zie eventueel ook de pagina "Uitcirkels", ivm. het Apollonius-punt.
[einde Opmerking]

2. Existentie van de Soddy-cirkels terug
We zullen hieronder aantonen, dat er inderdaad twee cirkels bestaan die aan de drie gegeven cirkels raken.
Deze raakcirkels worden Soddy-cirkels genoemd, naar Sir Frederick Soddy (zie paragraaf 4).

2.1. De middelpunten A1, A2, A3 niet collineair terug
We kiezen een inversie d met een van de drie raakpunten als centrum (zie figuur 2).

figuur 2 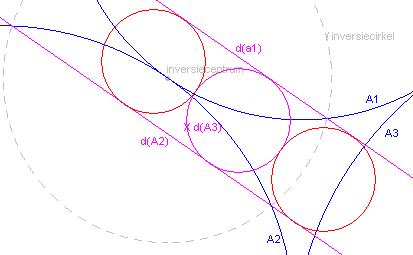soddy2 In de figuur hiernaast is het inversiecentrum het raakpunt van de cirkels A1 en A2.
De beide cirkels die dat punt als gemeenschappelijk raakpunt hebben gaan dan bij die inversie over in rechte lijnen, d(A1) en d(A2).
De derde cirkel gaat over in een cirkel, d(A3), die beide rechte lijnen raakt, en dus gelegen is tussen de rechte lijnen.
Er zijn nu twee cirkels die aan d(A1) en d(A2) en aan de beeldcirkel d(A3) raken.
De beelden van die cirkel onder de inversie d zijn de gezochte Soddy-cirkels.   ¨

2.2. De middelpunten A1, A2, A3 zijn collineair terug
Ook in dit geval kiezen we een inversie d met een van de drie raakpunten als centrum (zie figuur 3).

figuur 3 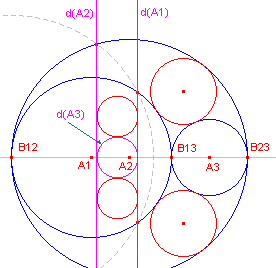soddy3 Hiernaast is het centrum van inversie het raakpunt B12.
Bij juiste keuze van de inversiecirkel gaan de cirkels A1 en A2 in twee evenwijdige rechte lijnen, d(A1) en d(A2).
Cirkel A3 gaat dan over in een tussen die lijnen gelegen, aan beide lijnen rakende, cirkel, d(A3).
Ook nu zijn er twee cirkels die aan de lijnen d(A1) en d(A2) en aan de beeldcirkel d(A3) raken.
De inversen van deze cirkels zijn dan weer de Soddy-cirkels.  ¨

Opmerking
Zie voor deze laatste configuratie ook de pagina "Arbelos".
[einde Opmerking]

3. Cirkelstelling van Descartes terug
In november 1643 beschreef René Descartes (1596-1650, Frankrijk) in een brief aan Prinses Elisabeth van Bohemen de relatie tussen de krommingen van vier elkaar rakende cirkels.
De kromming van een cirkel met straal R is gelijk aan 1/R.
Daarbij geldt, dat de kromming van een cirkel negatief wordt genomen als een cirkel de andere drie omvat (dus bij de grootste van de beide Soddy-cirkels; zie figuur 1).
De cirkelstelling van Descartes luidt:

Stelling 1
Raken de cirkels Ci, met i = 1...4, elkaar in zes verschillende punten en is de kromming van Ci gelijk aan ki, dan geldt:
   imagessoddy_f2

Bewijs:
[1] Zie de pagina "Cirkelstelling van Descartes" voor een direct analytisch bewijs.
[2] We geven hieronder een toepassing die in 1842 gevonden is door Philip Beecroft (Engeland) en waarmee het bewijs van de Cirkelstelling eveneens geleverd kan worden.

Uitgaande van de cirkels Ci zijn er namelijk een tweede serie Di van vier cirkels die elkaar twee aan twee raken.
D1 is de cirkel door de raakpunten van C2, C3, C4.
D2 is de cirkel door de raakpunten van C1, C3, D4.
D3 is de cirkel door de raakpunten van C1, C2, D4.
Als de middelpunten van C1, C2, C3 een driehoek ABC vormen, dan is D4 de incirkel of één van de uitcirkels van driehoek ABC (zie figuur 4).

figuur 4 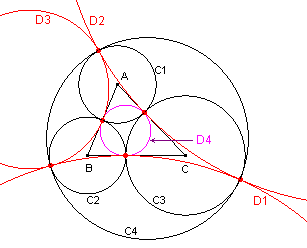soddy4 Geval a: D4 is de incirkel
Voor de krommingen ki van Ci (i=1..3) hebben we nu:
k1 = 1/(s-a), k2 = 1/(s-b), k3 = 1/(s-c)
Voor de kromming m4 van D4 geldt: m4 = ± 1/r.

Een gevolg van de formule van Heron (zie de pagina "Formule van Heron") is:
   r2 = (s-a)(s-b)(s-c)/s.

Nu is
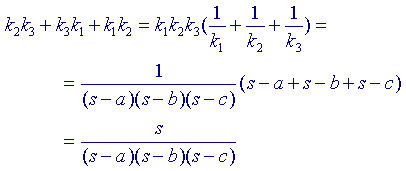
   imagessoddy_f3
Deze laatste uitdrukking is dus op basis van het gevolg van de formule van Heron (zie boven) gelijk aan m42.
Op dezelfde manier kunnen we aantonen dat voor de krommingen mi van Di (i=1..3) geldt:
   m2m3 + m3m1 + m1m2 = k42
Uiteraard kunnen we de subscripts in beide gevallen permuteren over 1, 2, 3 en 4.
Dus:
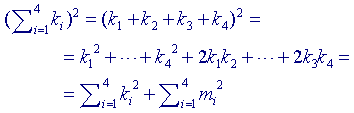   soddy_f4  ...... (1)
Het rechter lid is symmetrisch in k en m, dus geldt ook:
   imagessoddy_f8
waaruit we vinden
   soddy_f5...... (2)
We bekijken nu de uitdrukking (k1+k2+k3+k4)(k1+k2+k3-k4).
Herleiding hiervan geeft:
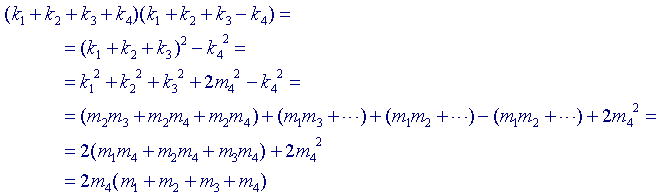
   soddy_f6
waaruit via identiteit (2) volgt
    k1 + k2 + k3 - k4 = 2m4
Tellen we de vier uitdrukkingen die hieruit door permutatie kunnen ontstaan, na kwadratering bij elkaar op, dan vinden we:
   soddy_f7

Blijkens (1) geldt dan:
   imagessoddy_f9

Geval b: D4 is een uitcirkel
In dit geval verloopt het bewijs geheel analoog aan het bewijs voor de incirkel.
¨

Opmerking
Zie
H.S.M. COXETER, Introduction to Geometry, John Wiley & Sons, Inc., 1969, pg. 14-15.
[einde Opmerking]

4. Sir Frederick Soddy terug
Sir Frederick Soddy (1877-1956, Engeland) kreeg in 1921 de Nobelprijs voor scheikunde voor zijn ontdekking van isotopen.
Hij heeft zich onder oa. ook beziggehouden met bijzondere wiskundige vraagstukken. Zo ook dus zijn herontdekking in 1936 van de Cirkelstelling van Descartes, die hij met een gedicht (de eerste twee hieronder vermelde strofen) aankondigde in het tijdschrift Nature.
Enige tijd later vulde hij het gedicht aan met de derde strofe: de stelling geldt ook in de 3-dimensionale ruimte.

The Kiss Precise
by Frederick Soddy
Continued
For pairs of lips to kiss maybe
Involves no trigonometry.
'Tis not so when four circles kiss
Each one the other three.
To bring this off the four must be
As three in one or one in three.
If one in three, beyond a doubt
Each gets three kisses from without.
If three in one, then is that one
Thrice kissed internally.		 Four circles to the kissing come.
The smaller are the benter.
The bend is just the inverse of
The distance form the center.
Though their intrigue left Euclid dumb
There's now no need for rule of thumb.
Since zero bend's a dead straight line
And concave bends have minus sign,
The sum of the squares of all four bends
Is half the square of their sum.

In Nature, June 20, 1936 (#137), p. 1021		 To spy out spherical affairs
An oscular surveyor
Might find the task laborious,
The sphere is much the gayer,
And now besides the pair of pairs
A fifth sphere in the kissing shares.
Yet, signs and zero as before,
For each to kiss the other four
The square of the sum of all five bends
Is thrice the sum of their squares.

In Nature, 1937 (#139), p. 62
   Vier cirkels doen een rondedans,
De kleinste zijn het kromste.
De kromming is het omgekeerde van
De afstand tot het middelpunt.
Hoewel hun intrige Euclides met stomheid sloeg
Zijn vuistregels nu overbodig.
Omdat een nulkromming een rechte lijn is
En concave krommingen een minteken hebben,
Is de som der kwadraten van alle vier de krommingen
de helft van het kwadraat van hun som.

Vertaling: Bettelou Los, in
David Wells, Woordenboek van merkwaardige en
interessante meetkunde,
Uitgeverij Bert Bakker, Amsterdam, 1993		   

Een half jaar na Soddy's eerste publicatie werd, eveneens in Nature, een strofe aan het gedicht toegevoegd door Thorold Gosset (1869-1962), waarin deze een generalisatie aankondigde voor n+2 hypersferen in een n-dimensionale ruimte; blijkbaar geldt voor n+2 elkaar twee aan twee rakende n-dimensionale hypersferen:
   imagessoddy_fn

The Kiss Precise (generalized)
by Thorold Gosset
And let us not confine our cares
To simple circles, planes and spheres,
But rise to hyper flats and bends
Where kissing multiple appears,
In n-ic space the kissing pairs
Are hyperspheres, and Truth declares -
As n + 2 such osculate
Each with an n + 1 fold mate
The square of the sum of all the bends
Is n times the sum of their squares.

In Nature, January 9, 1937

5. Isoperimetrisch punt terug

Definities
[1]
Een isoperimetrisch punt van een driehoek ABC is een punt (in het vlak van de driehoek) waarvoor de omtrekken van de driehoeken PAB, PBC en PCA gelijk zijn.
[2]
Het tweede (buitenste) punt van Soddy is het middelpunt van de omgeschreven Soddy-cirkel van een driehoek.
.
Stelling 2
Het tweede punt van Soddy is een isoperimetrisch punt van een driehoek.

Bewijs: zie figuur 5.

figuur 5 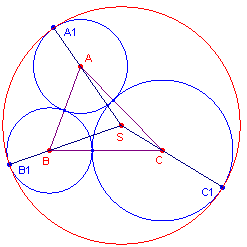soddy5 Zij R de straal van de grote Soddy-cirkel.
Nu is
SA = R - (s - a) = R - s +a
SB = R - s + b
SC = R - s + c.
Zodat
[SABS] = R - s + a + c + R - s + b
= 2R - 2s + a + b + c
= 2R

We kunnen op dezelfde manier bewijzen, dat [SBCS] = [SCAS] = 2R.
Het punt S is dus een isoperimetrisch punt van driehoek ABC. ¨

Opmerking
Een noodzakelijke en voldoende voorwaarde voor het bestaan van het isoperimetrisch punt is   a + b + c > 4R + r
(Veldkamp, 1985).
[einde Opmerking]

6. Tenslotte terug
Zonder bewijs vermelden we nog

Stelling 3
Het uitwendig gelijkvormigheidspunt van de beide Soddy-cirkels is het punt van Gergonne van de driehoek (het snijpunt van de verbindingslijnen tussen een hoekpunt en het raakpunt van de incirkel met de overstaande zijde van dat hoekpunt).
Het inwendig gelijkvormigheidspunt van de Soddy-cirkels is het incentrum van de driehoek.
.
figuur 6 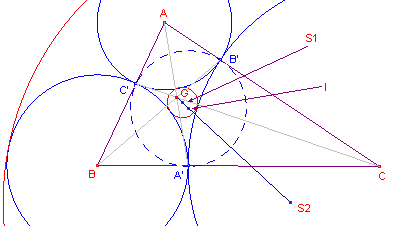soddy6 In nevenstaande figuur:
- G is het punt van Gergonne van de driehoek;
- I is het incentrum van de driehoek.
- S1 en S2 zijn de middelpunten van de Soddy-cirkels

G, I, S1 en S2 zijn daarom dus collineair.
Stelling 3 is bewezen door A. Vandeghen en G.R. Veldkamp: American Mathematical Monthly, #71, 1964, pag. 178).
Zie ook:
G.R. VELDKAMP:"The Isoperimetric Point and the Point(s) of Equal Detour", Amer. Math. Monthly,  #92, 1985, pag. 546-558.

Afstand tussen Soddy-cirkels
Voor niet-snijdende cirkels, zoals de Soddy-cirkels, kan een "afstand" worden gedefinieerd.
Klik hier voor de pagina "Middencirkel".
Klik hier voor de pagina "Inverse afstand".

begin pagina
[soddy.html] laatste wijziging op: 27-12-04