Middencirkel

Overzicht ][ Inverse afstand | Inversie | Meetkunde

0. Overzicht

Inleiding
Middencirkel (ook wel machtcirkel)
     2.1. Snijdende cirkels
     2.2. Direct bewijs
     2.3. Bewijs met inversie
Alle gevallen
     3.1. Snijdende cirkels
     3.2. Uitwendig rakende cirkels
     3.3. Niet-snijdende cirkels (buitenliggend)
     3.4. Inwendig rakende cirkels
     3.5. Niet-snijdende cirkels (binnenliggend, niet-concentrisch)
     3.6. Concentrische cirkels
Cirkels met gelijke straal
Referenties
Download

Zie ook de Cabri-werkbladen "Loodrecht snijden" en "Inversie"
Zie ook de webpagina’s "Inversie" en "De macht van een punt tov. een cirkel"

1. Inleiding

Definities
[1]
Twee cirkels heten orthogonaal als ze elkaar loodrecht snijden.
De eerste cirkel heet soms ook wel een orthogonaal-cirkel van de tweede cirkel.
[2]
Twee punten A en B heten elkaars inverse tov. een cirkel (O, k) indien OA.OB = k².
De cirkel heet inversiecirkel. Het punt O heet centrum van inversie.
Het getal k² heet inversiemacht.
(zie voor deze definities ook de pagina "Inversie")

figuur 1

Opmerking
Een cirkel heeft meerdere orthogonaalcirkels (een cirkelbundel); zie figuur 1.
[einde Opmerking]

Tussen inversie en orthogonaliteit van cirkels is een verband.

Stelling 1
Als de cirkel (P, r) een orthogonaalcirkel is van de cirkel (O, k), dan is dan wordt de cirkel P door de inversie tov. de cirkel O op zichzelf (niet puntsgewijs) afgebeeld.
De cirkelboog binnen de inversiecirkel wordt afgebeeld op de cirkelboog buiten de inversiecirkel.

Bewijs:

figuur 2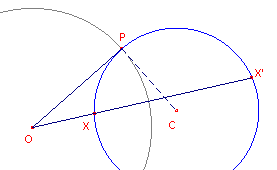

Cirkel O is de inversiecirkel.
Voor X en X’ geldt:
OX . OX’ = OP² = k²
De punten X en X’ zijn dus elkaars beeld bij de inversie met centrum O en macht k².

2. Middencirkel

2.1. Snijdende cirkels

We gaan (eerst) uit van twee elkaar snijdende cirkels.
We vragen ons af of het mogelijk is de ene cirkel op de andere cirkel af te beelden door inversie.
Op de pagina "Inversie", paragraaf 5.2, Stellling 2, staat:

Stelling 2
Ligt O niet op de cirkel K, en is m de macht van O tov. K, dan gaat K bij inversie (O, k²) over in een cirkel die vermenigvuldigingsfiguur is van K met factor k²/m.

Voor het bewijs verwijzen we naar de hierboven genoemde paragraaf op de pagina "Inversie".

figuur 3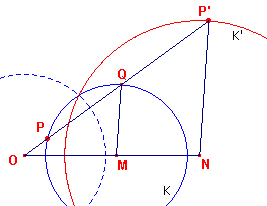

De inversiecirkel is dus de cirkel die gaat door de beide snijpunten.
Het middelpunt van de inversiecirkel is (in dit geval) het uitwendig gelijkvormigheidspunt van de cirkels.

Definitie
De inversiecirkel heet middencirkel (Eng.: mid-circle) van beide cirkels.
De inversiecirkel wordt ook wel machtcirkel genoemd.
In Engelse literatuur wordt de middencirkel vaak aangeduid als 'circle of antisimilitude'.

2.2. Direct bewijs
We kunnen natuurlijk ook direct bewijzen dat zo’n middencirkel bestaat (zie figuur 4).

figuur 4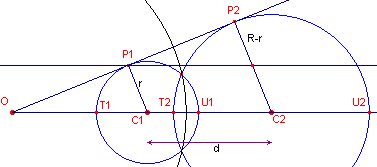

In figuur 4 is O het uitwendig gelijkvormigheidspunt van beide cirkels.
Nu is:
OC₁ : OC₂ = r : R
waarbij r en R de stralen zijn van de cirkels.
Dus geldt:
OC₂ = R/r^.OC₁.

Voor OC₁ geldt dan:
   OC₁ + d = R/r^.OC₁
zodat

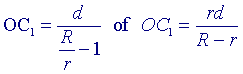
Nu is

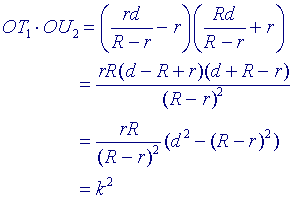
OT₁.OU₂ = constant. T₁ en U₂ zijn dus elkaars inverse tov. een cirkel met O als middelpunt.
In het bijzonder geldt (zie figuur 5):

figuur 5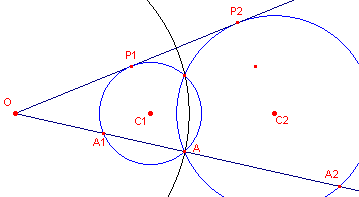

   (OP1)². (OP2)² = (k²)² = k⁴
terwijl
   OA₁^.OA = OP₁² en OA^.OA₂ = OP₂²
Zodat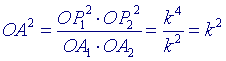

De straal van de inversiecirkel is dus OA.

Opmerking
Er is in dit geval nog een tweede middencirkel, nl. de cirkel die bepaald wordt door het inwendig gelijkvormigheidspunt van beide cirkels.
We spreken van uitwendige en inwendige middencirkels.
[einde Opmerking]

2.3. Bewijs met inversie

figuur 6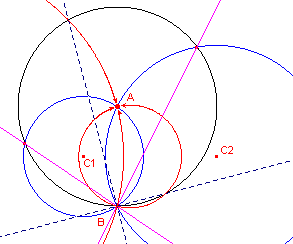

In figuur 6 is cirkel (A, AB) een inversiecirkel.
De inverse beelden van de cirkels C₁ en C₂ zijn twee rechte lijnen (immers de cirkels gaan door het middelpunt van de inversiecirkel).
De lijnen snijden elkaar in het punt B.
Deze lijnen kunnen op twee manieren (nl. via de bissectrices van de hoeken) op elkaar worden afgebeeld.
De inverse beelden van deze lijnen zijn twee cirkels, de middencirkels van C₁ en C₂.

Twee snijdende cirkels hebben dus twee middencirkels.

Gevolg
Omdat inversie een hoektrouwe (conforme afbeelding) is, volgt uit het bovenstaande, dat de middencirkels de hoeken tussen de beide gegeven cirkels middendoor delen.
En ook: de beide middencirkels snijden elkaar loodrecht (orthogonaalcirkels).
[einde Opmerking]

3. Alle gevallen

We kunnen de volgende gevallen onderscheiden (zie figuur 7):

1. snijdende cirkels
2. uitwendig rakende cirkels
3. niet-snijdende cirkels (buitenliggend)
4. inwendig rakende cirkels
5. niet-snijdende cirkels (binnenliggend, niet-concentrisch)

figuur 7

7.1	7.2	7.3	7.4	7.5

6. concentrische cirkels

We gaan er bij de constructies van uit, dat de cirkels ongelijke stralen hebben.
Voor cirkels met gelijke straal zie paragraaf 4.

3.1. Snijdende cirkels
Zie hiervoor paragraaf 2.

3.2. Uitwendig rakende cirkels

figuur 8a		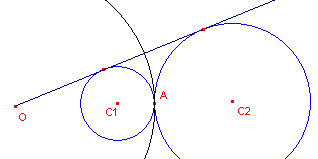Zonder inversie Ook in dit geval kunnen we het uitwendig gelijkvormigheidspunt O vinden via de gemeenschappelijke (uitwendige) raaklijnen. De inversiecirkel is dan de cirkel met O als middelpunt die gaat door het raakpunt (zie figuur 8a).
figuur 8b		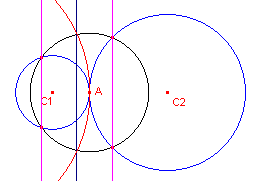Met inversie De cirkel met middelpunt A is inversiecirkel. Door de inversie tov. deze cirkel gaan de beide cirkels over in evenwijdige rechte lijnen. Deze worden door de middenparallel van deze lijnen op elkaar afgebeeld.

Het inverse beeld van de middenparallel van beide lijnen is dus middencirkel van beide gegeven cirkels.

3.3. Niet-snijdende cirkels (buitenliggend)

figuur 9a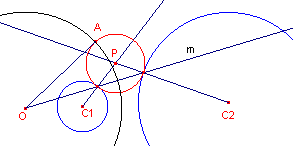

Zonder inversie
Ook hier is het middelpunt van de middencirkel het uitwendig gelijkvormigheidspunt. Probleem is echter dat we nu (in tegenstelling tot de vorige gevallen) het punt A niet direct kunnen vinden.
We gebruiken echter een cirkel die beide cirkels raakt (cirkel met middelpunt P).

Cirkel P is gevonden door een willekeurige lijn m door O te snijden met de beide cirkels en twee snijpunten te gebruiken voor de constructie van het punt P.
Cirkel P moet door de inversie op zichzelf worden afgebeeld (hoektrouw). A is dus het raakpunt van de raaklijn uit O aan deze cirkel.

Met inversie
Twee niet snijdende cirkels kunnen door inversie worden afgebeeld op twee concentrische cirkels (zie Hulpstelling 2 op de pagina "Een probleem van Steiner").

figuur 9b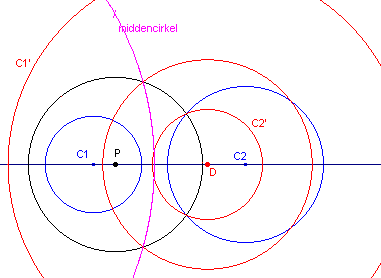

In figuur 9b zijn C₁’ en C₂’ de (concentrische) beelden van C₁ en C₂ bij een inversie met centrum P.
Bij een inversie met de cirkel met middelpunt D en straal Ö(ab) gaan C₁’ (met straal a) en C₂’ (met straal b) in elkaar over (zie paragraaf 3.6).
Het inverse beeld van deze cirkel bij inversie met centrum P is de gevraagde middencirkel van C₁ en C₂.

3.4. Inwendige rakende cirkels

figuur 10a		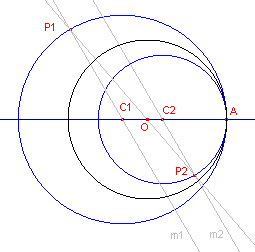Zonder inversie Evenals in paragraaf 3.2 (Uitwendig rakende cirkels) kunnen ook hier gebruik maken van het (dit keer) inwendig gelijkvormigheidspunt O. De constructie daarvan is in figuur 10a gevonden met de evenwijdige lijnen m₁ en m₂. De middencirkel van de beide cirkels is dan cirkel (O,OA).
figuur 10b		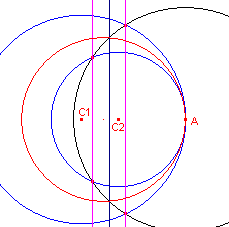Met inversie De constructie verloopt op dezelfde manier als in paragraaf 3.2 (Uitwendig rakende cirkels).

3.5. Niet-snijdende cirkels (binnenligend, niet-concentrisch)

figuur 11a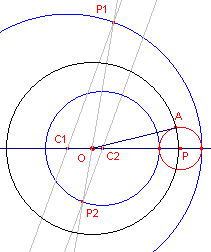

Zonder inversie
Evenals in paragraaf 3.4 kunnen we het inwendig gelijkvormigheidspunt O vinden met behulp van twee evenwijdige lijnen door de middelpunten van C₁ en C₂.
Cirkel P raakt aan C₁ en C₂.
Deze cirkel moet door de gezochte middencirkel op zichzelf worden afgebeeld.
De middencirkel is dus een orthogonaalcirkel van cirkel P met middelpunt O.
De straal van de middencirkel is dus OA.
Zie ook paragraaf 3.3.

Met inversie
Ook nu maken we gebruik van het feit, dat twee niet-snijdende cirkels via een inversie kunnen worden afgebeeld op twee concentrische cirkels (zie ook paragraaf 3.3).
Als inversiecirkel is in figuur 11b de cirkel met middelpunt P gebruikt (zie Hulpstelling 2 op de pagina "Een probleem van Steiner").

figuur 11b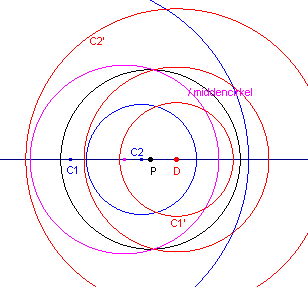

De middencirkel van de concentrische cirkels wordt dan door deze inversie afgebeeld op de middencirkels van de gegeven cirkels.

3.6. Concentrische cirkels
Bij concentrische cirkels gaan we iets anders te werk.
Het is duidelijk, dat het gemeenschappelijk middelpunt C het inwendig gelijkvormigheidspunt van deze cirkels is.
De gezochte middencirkel heeft punt C dus eveneens als middelpunt.

figuur 12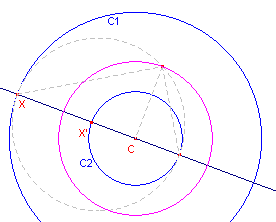

Voor de punten X en X’ moet nu gelden
CX^.CX’ = k²
waarbij k de lengte van de straal is van de gezochte middencirkel.
k is dus middelevenredig tussen CX en CX’, die opvolgend gelijk zijn aan de straal a en de straal b van C₁ en C₂.
De straal k van de middencirkel is in dit geval dus gelijk aan Ö(ab).

Zie ook de pagina "Inverse afstand".

4. Cirkels met gelijke straal

figuur 13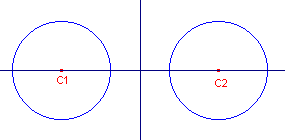

Bij cirkels met gelijke straal (en niet samenvallend middelpunt) is het uitwendig gelijkvormigheidspunt het oneigenlijk punt van de centraal (de verbindingslijn van de middelpunten).

De middencirkel van deze cirkel ontaardt daardoor in een rechte lijn: de middelloodlijn van de afstand tussen de middelpunten.

Met deze kennis kunnen we eenvoudig een inversie vinden die twee cirkels afbeeldt op twee cirkels met gelijke straal (zie figuur 14). We kiezen het inversiecentrum namelijk op de middencirkel.

figuur 14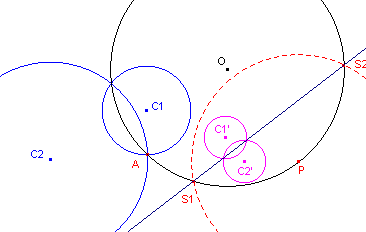

Cirkel O is de middencirkel van C₁ en C₂.
Cirkel P is de inversiecirkel (P ligt op de middencirkel van C₁ en C₂).
De lijn S₁S₂ is het beeld van de middencirkel bij deze inversie.
Deze lijn is dus "spiegelas" van de beelden C₁’ en C₂’ van C₁ en C₂.

5. Referenties

[1]	H.S.M. COXETER, S.L. GREITZER, Geometry Revisited, MAA (vol. 19), 1967
[2]	R. DIXON, Mathographics, Dover Publications, New York, 1987
[3]	D. PEDOE, Circles: A mathematical view, MAA (Spectrum Series), 1957
[4]	FLOOR. VAN LAMOEN: De Porisme-cirkels (website)
[5a]	Webpagina "Inversie" / Cabri-werkblad "Inversie"
[5b]	Webpagina "Inverse afstand"
[5c]	Webpagina "Loodrecht snijden" (Cabri-werkblad)
[5d]	Webpagina "De macht van een punt tov. een cirkel"
[7]	Steiner’s porisma op de webpagina "Een probleem van Steiner"

6. Download
Deze pagina is, in een iets andere vorm, ook in PDF-formaat beschikbaar.
midcirkel.pdf [ca. 110Kb]

Een PDF-bestand kan met Acrobat^® Reader worden gelezen:

[midcirkel.htm] laatste wijziging op: 18-07-08