Een probleem van Steiner

Inleiding | Formulering probleem | Hulpstellingen | Bewijs | Verwijzingen   ][  Inversie | Meetkunde

1. Inleiding
Het probleem, dat afkomstig is van  Jakob Steiner (1796-1863, Zwitserland) betreft de volgende figuur.

figuur 1  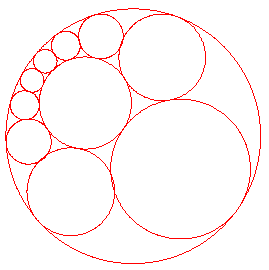steinerinv1 Hierin zien we twee niet-snijdende cirkels, met daar tussen een aantal cirkels die beide cirkels raken en telkens twee aan twee elkaar.
Beginnen we in figuur 1 bij een cirkel uit deze rij, dan zien we dat de laatste cirkel in de rij de eerste cirkel eveneens raakt.
Dat dit niet noodzakelijk is kan worden ingezien, door de straal van de grootste cirkel iets te vergroten.

Opmerking
Dit probleem wordt in de wiskundige literatuur ook wel aangeduid als Steiner's porisma (zie stelling 1).
[einde Opmerking]

2. Formulering van het probleem

Definitie
Een rij van Steiner-cirkels is een  n-tal cirkels Ci die elk raken aan twee vaste, niet snijdende cirkels en aan Ci-1 en Ci+1 uit deze verzameling, terwijl Cn raakt aan C1.
.
Stelling (Steiner's porisma)
Als twee cirkels een Steiner-rij toelaten, dan staan ze een oneindig aantal verschillende Steiner-rijen toe, bestaande uit hetzelfde aantal cikels.

Klik hier Animatie voor een animatie van een Steiner-rij bestaande uit 3 cirkels.
Klik hier Animatie voor een animatie bestaande uit 8 cirkels.

3. Hulpstellingen

Bij het bewijs van het bovenstaande probleem van Steiner gebruiken we de volgende tweetal hulpstellingen:

Hulpstelling 1
Zijn C1 en C2 twee gegeven niet-snijdende cirkels met machtlijn m, waarop de punten A en B liggen
De cirkels D1 en D2 met middelpunten A en B die C1 en C2 loodrecht snijden, snijden de centraal van C1 en C2 in twee punten.

Opmerking. De beide punten worden wel de punten van Poncelet (naar Jean Victor Poncelet, 1788-1867, Frankrijk) of ook wel grenspunten genoemd. Zie ook het Cabri-werkblad 'Cirkelbundels'.

Bewijs: zie figuur 2.

figuur 2  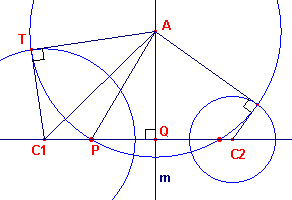steinerinv2 In deze figuur bekijken we alleen de cirkel D1 met middelpunt A en straal r..
Nu is:
   AC12 = AT 2 + r2
De lijn m snijdt de centraal in Q. Dan is
   AC12 = AQ2 + C1Q2
Omdat de beide cirkels elkaar niet snijden, is: C1Q > r, waaruit dan volgt:
   AT > AQ
De cirkel met middelpunt A (D1) snijdt de centraal dus in twee punten, waarvan het punt P er één is.

We bewijzen vervolgens, dat de ligging van het punt P onafhankelijk is van de ligging van het punt A op m.

   AP2 = PQ2 + QA2
   AP2 = AT 2 = AC12 - C1T 2 = (C1Q2 + QA2) - C1T 2
Dus:
   PQ2 = C1Q2 - C1T 2
De ligging van het punt P (en dus ook die van het tweede punt P2) is dus onafhankelijk van de ligging van het punt A op m.
Klik hier Animatie voor een illustratie van deze uitspraak.
De cirkel met middelpunt B (op m) gaat dus door de beide punten P (P1) en P2. ¨

Hulpstelling 2
Er is een inversie die twee gegeven niet-snijdende cirkels afbeeldt op twee concentrische cirkels.

Bewijs: zie figuur 3.

figuur 3  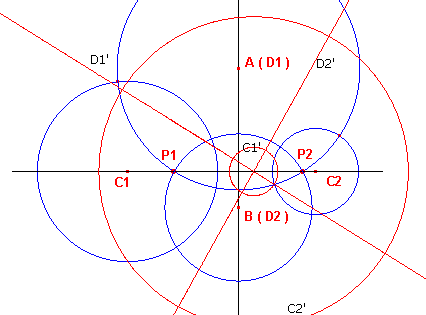steinerinv3 We kiezen P1 (of P2) als centrum van inversie (de inversiecirkel is niet getekend in figuur 3).
Omdat D1 en D2 door P1 gaan, worden deze cirkels afgebeeld op twee snijdende rechte lijnen D1' en D2'.
De cirkels C1 en C2 worden afgebeeld op de cirkels C1' en C2'.
Omdat de cirkels D1, D2 de cirkels C1, C2 loodrecht snijden, snijden ook de lijnen D1' en D2' de beide cirkels C1' en C2' loodrecht (het zijn middellijnen van beide).

Waarmee het gestelde is aangetoond. ¨

4. Het bewijs van het probleem van Steiner

figuur 4  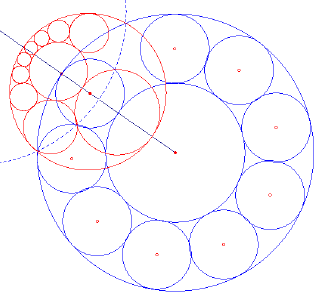steinerinv4 Volgens Hulpstelling 2 kunnen twee niet-snijdende (niet-concentrische) cirkels worden geïnverteerd in twee concentrische cirkels.
De Steiner-rij gaat daarbij over in een Steiner-rij die bestaat uit gelijke cirkels, immers de elementen van de rij raken alle aan de beide concentrische cirkels.
Deze tweede rij kan binnen die cirkels (binnen de "ring") oneindig vaak worden geroteerd.
Dit geldt dus ook voor de inverse daarvan. ¨

5. Verwijzingen
Op de volgende webpagina's wordt ook aandacht besteed aan Steiner's porisma.

[1]     Inverse afstand
[2] Soddy-cirkels
[3] Cabri-werkblad "Inversie"

up

[steinerinv.htm] laatste wijziging op: 15-07-2008