Inverse afstand

Overzicht  ][  Middencirkel | Inversie | Meetkunde

0. Overzicht begin pagina

  1. Inleiding
         1.1. Definities en stellingen
         1.2. Rakende en snijdende cirkels
  2. Rekenen aan Steiner's porisma
  3. Rekenen aan de i-afstand
  4. Toepassingen
         4.1. Om- en incirkel
         4.2. Omcirkel en negenpuntscirkel
  5. Referenties
  6. Download

1. Inleiding begin pagina
1.1. Definities en stellingen begin pagina
We definiëren:

Definitie
Voor twee concentrische cirkels C1 (straal a) en C2 (straal b) is de c-afstand het getal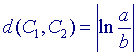
   Image178.
.
Stelling 1
Voor de straal r van de middencirkel Cm van twee concentrische cirkels (met stralen a en b) geldt
   Image179.
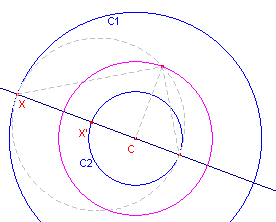figuur 1 Image180 Bewijs:
Zie de pagina "Middencirkel".¨

We hebben nu verder:

Stelling 2
De middencirkel van twee concentrische cirkels deelt de c-afstand van die cirkels middendoor.

Opmerking: Voor het begrip "middencirkel" zie de pagina "Middencirkel".

Bewijs:
We hebben
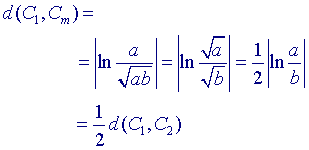
   Image181
¨

Er geldt eveneens:

Stelling 3
Twee niet-snijdende cirkels kunnen door een inversie worden afgebeeld op twee concentrische cirkels.

Bewijs:
Zie Hulpstelling 2 op de pagina "Een probleem van Steiner". ¨

Ook voor twee niet-snijdende cirkels kunnen we, op basis van deze stelling een "afstands"-definitie geven:

Definitie
Onder de i-afstand (inverse afstand) van twee niet-snijdende cirkels C1 en C2 verstaan we het getal d(C1, C2) dat gelijk is aan de c-afstand van de concentrische (inverse) beelden C1’ en C2’ van C1 en C2.

Opmerking
Als er geen verwarring kan ontstaan worden kunnen de begrippen "c-afstand" en "i-afstand" door elkaar worden gebruikt.
[einde Opmerking]

1.2. Rakende en snijdende cirkels begin pagina
Rakende cirkels worden door een inversie met het raakpunt als inversiecentrum, afgebeeld op twee evenwijdige lijnen (zie de pagina "Middencirkel").

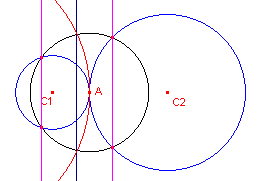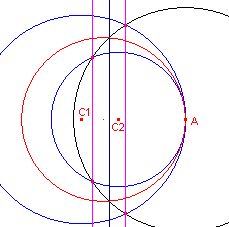figuur 2 Image182 Image183

Evenwijdige lijnen op hun beurt kunnen worden opgevat als het limietgeval van twee concentrische cirkels (het middelpunt is het punt-op-oneindig van de centraal).
We kunnen daardoor zonder problemen afspreken:

Afspraak
Rakende cirkels hebben een i-afstand gelijk aan 0.

Voor snijdende cirkels geven we geen definitie.

2. Rekenen aan Steiner’s porisma

 begin pagina
Steiner’s porisma is behandeld op de pagina "Een probleem van Steiner".
figuur 3 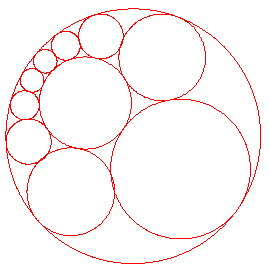Image184 We hebben twee niet-snijdende cirkels (binnenliggend) en een aantal (n) cirkels die beide cirkels en elkaar opvolgend raken.
We kunnen de twee niet-snijdende cirkels afbeelden op twee concentrische cirkels.
De andere cirkels vormen dan een ring van n congruente cirkels, waarvan de middelpunten een regelmatige n-hoek vormen (zie figuur 4, waarin n = 6).
figuur 4 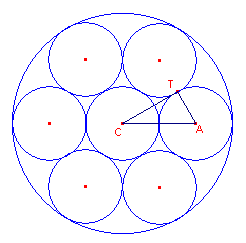Image185 We gaan uit van een regelmatige n-hoek.
Zij nu A een van de middelpunten van de cirkels in de ring, en T het raakpunt met een buurcirkel.
Zij verder a de straal van de buitenste cirkel (C1) en b de straal van de binnenste cirkel (C2).
Dan is CA = (a + b) /2 en AT = (a - b) / 2.
In driehoek ACT is Ð ACT = p/n.
Verder is dan d = d(C1,C2) = ln(a/b)

We hebben nu in driehoek ACT:
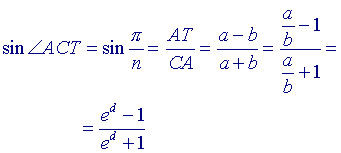
   Image186
Lossen we hieruit d op dan vinden we eerst
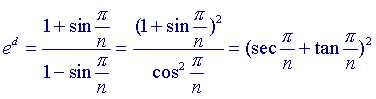
   Image187
zodat
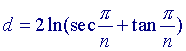
   Image188

Voorbeelden


[1]
Voor n = 4 hebben we dus d = 2 ln (Ö 2 + 1).
figuur 5a 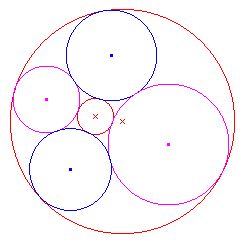Image189 We hebben nu een configuratie van zes cirkels die in drie paren "overliggende" cirkels uiteen kan vallen.
Elke cirkel raakt hierbij aan de andere met uitzondering van z’n overliggende cirkel
De i-afstand van elk paar overliggende cirkels is gelijk aan 2 ln (Ö2 + 1), terwijl de overige afstanden gelijk zijn aan 0.

[2]
Soddy-cirkels
figuur 5b 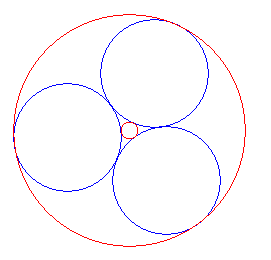Image190 Deze cirkels worden behandeld op de pagina "Soddy-cirkels".
De configuratie is die uit het porisma van Steiner voor n = 3 (zie figuur 5b).
Dus d = 2 ln(sec p/3 + tan p/3) = 2 ln(2 + Ö3)

[3]


Uitdrukkingen voor de i-afstand met hyperbolische functies
Uit
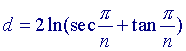
    Image188
volgt, als we in de tussenberekeningen j  = p/n stellen:
   Image191
Nu is:
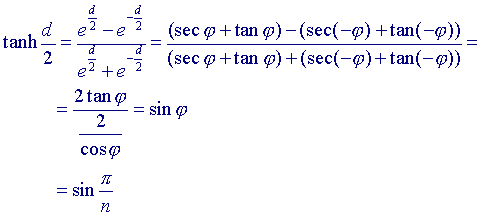
   Image192
Dus tanh d/2 = sin p/n.
Zo ook sinh d/2 = tan p/n en cosh d/2 = sec p/n.
Voor de Soddy-cirkels (zie voorbeeld 2) hebben we dus ook cosh d/2 = sec p/3 = 2.

3. Rekenen aan de i-afstand

 begin pagina
We gaan eerst even uit van twee snijdende cirkels C1 en C2 met stralen a en b.
De "echte" afstand tussen de middelpunten van C1 en C2 zij c.
figuur 6 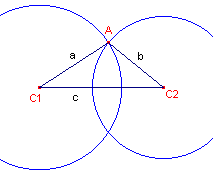Image193 Voor de scherpe hoek bij A (de hoek tussen de cirkels) geldt nu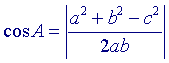
   Image194.

We bekijken nu de uitdrukking
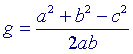
    Image195
als één van a, b of c groter is dan de som van de beide andere (in dit geval snijden de cirkels elkaar dus niet).

Concentrische cirkels - c = 0.
Voor de i-afstand d van de beide cirkels hebben we nu d = ln(a/b) voor a > b (zie figuur 7).

figuur 7 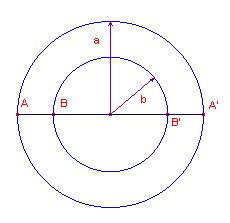Image196 Voor de eindpunten van de middellijnen AA’ en BB’ hebben nu de dubbelverhouding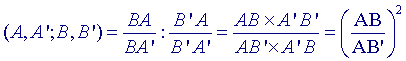
   Image197
Nu is AB = a - b en AB’ = a + b, zodat

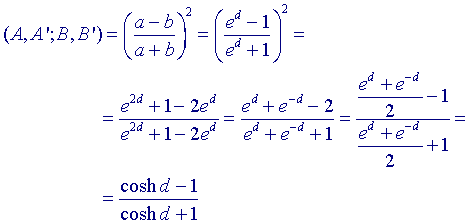
Image198

Doordat de dubbelverhouding invariant is bij inversie, geldt deze uitdrukking ook in het geval de concentrische cirkels verkregen zijn als beeld bij een inversie van twee niet-snijdende cirkels.
Echter dan moet de dubbelverhouding worden uitgedrukt in de termen van de werkelijke a, b en c.

Niet-concentrische cirkels - geval 1: a - b > c

figuur 8 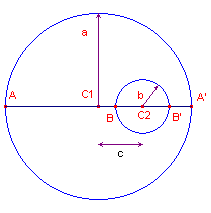Image199

Dus:
Image200
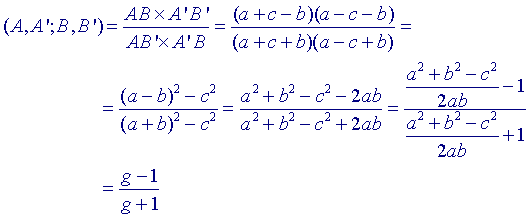
Dus cosh d = g.

Niet-concentrische cirkels - geval 2: a + b < c

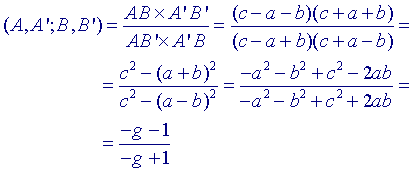
Image210
Dus cosh d = -g.

We hebben dus:

Stelling 4
Als c de "echte" afstand is tussen de middelpunten van twee elkaar niet-snijdende cirkels met stralen a en b, dan geldt voor de i-afstand d van beide cirkels: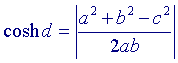
   Image202

Merk hierbij de overeenkomst op tussen de i-afstand van twee niet-snijdende cirkels en de hoek tussen twee snijdende cirkels.

4. Toepassingen

 begin pagina

4.1. Omcirkel en incirkel begin pagina

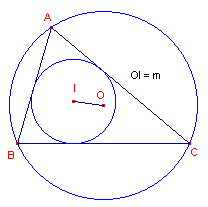figuur 9 Image203 Zij d de i-afstand van de om- en incirkel van een driehoek.
Zij R is de straal van de omcirkel en r de straal van de incirkel. Dan geldt: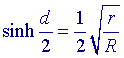
   Image204.

Voor de afstand m van de middelpunten van beide cirkels geldt:
    m2 = R2 - 2rR
Het bewijs van deze relatie staat op de pagina "Om- en incirkel".

Nu is volgens stelling 4:
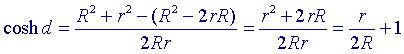
   Image205
Verder is
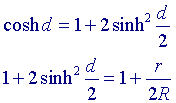
   Image206
waaruit het gestelde volgt.¨

4.2. Omcirkel en Negenpuntscirkel begin pagina

figuur 10 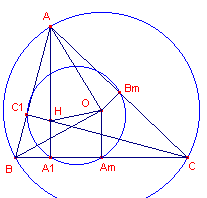Image207 Zij d de i-afstand van de omcirkel en de negenpuntscirkel van een driehoek.
Voor een scherphoekige driehoek ABC geldt
   sinh2 ½d = cosA cosB cosC
Voor een stomphoekige driehoek ABC geldt
   sinh2 ½d = - cosA cosB cosC

We gaan uit van een scherphoekige driehoek ABC waarvan de straal van de omcirkel gelijk is aan R.
In driehoek OBA m geldt: Ð A mOB = A.
Uit OA m / R = cosA volgt dan AH = 2RcosA.
In driehoek AHO geldt dan volgens de cosinusregel: HO2 = AH2 + OA2 - 2AH . OH . cosÐ OAH, zodat
HO2 = 4R2cos2A + R2 - 4R2 . cosA . cosÐ OAH …… (1)
In driehoek A1AC is Ð A1AC = 90º - C.
In driehoek OB mA is Ð B mAO) = 90º - B
zodat
Ð A1AO = Ð OAH  = B - C (mits B > C hetgeen de algemene geldigheid niet aantast).
Vergelijking (1) gaat daardoor dus over in
   HO2 = R2(1 + 4cos2A - 4 . cosA . cos(B - C) ) =
           = R2(1 + 4cosA . ( -cos(B + C) - cos(B - C) )
           = R2(1 + 4cosA . (-2cosB . cosC))
Dus
   HO2 = R2(1 - 8cosA . cosB . cosC)
Voor de straal r van de negenpuntscirkel geldt r = ½ R, terwijl voor het middelpunt N van de negenpuntscirkel geldt: ON = ½ OH.
Volgens stelling 4 vinden we dan
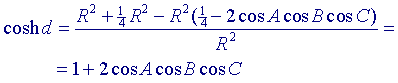
   Image208
Wegens 2sinh2  ½x = cosh x - 1 hebben we dan
   sinh2 ½d = cosA cosB cosC
¨

5. Referenties begin pagina
Zie de pagina "Middencirkel"

6. Download begin pagina
Deze pagina is, in een iets andere vorm, ook beschikbaar in PDF-formaat.
Download invafstand.pdf [ca. 68Kb]

Een PDF-bestand kan met Acrobat® Reader worden gelezen: Get Acrobat® Reader

begin pagina

[invafstand.htm] laatste wijziging op: 18-07-08