Cabri werkblad

Overzicht  ][  Alle werkbladen | Hyperbolische meetkunde | Meetkunde | Cabri

Overzicht - Loodrecht snijden

  1. Definities
  2. Loodrecht snijdende cirkels
         Opdracht 1
         Opdracht 2
  3. Interludium
         Opdracht 3
         Opdracht 4
  4. Verder onderzoek
         Opdracht 5
  5. Tenslotte
         Opdracht 6
         Opdracht 7, een macro (facultatief)
  6. Download

1. Definities
Allereerst de definitie voor de hoek tussen twee lijnen.

Definitie
Als twee rechte lijnen elkaar snijden, dan verstaan we onder de hoek tussen die twee lijnen de kleinste hoek die wordt gevormd door die lijnen.

Staan de lijnen loodrecht op elkaar, dan is de kleinste hoek (ze zijn alle vier aan elkaar gelijk) dus 90° .
In dit geval spreken we van loodrecht snijden (zie figuur 1 en figuur 2).
Als de lijnen evenwijdig zijn of samenvallen, dan zeggen we wel dat de hoek 0° is.

figuur 1 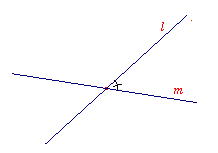loodr1      figuur 2 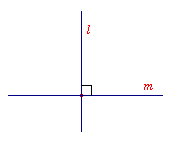loodr2

Maar wat te doen als een lijn en een cirkel of twee cirkels elkaar snijden?
Kunnen we dan ook spreken van de hoek waaronder ze elkaar snijden?

We geven een tweetal definities.
Definities
[1] Onder de hoek tussen een rechte lijn en een kromme lijn in een punt (een snijpunt van beide) verstaan we de hoek tussen die rechte lijn en de raaklijn in dat punt.
[2] Onder de hoek tussen twee kromme lijnen in een punt (een snijpunt van beide) verstaan we de hoek tussen de raaklijnen in dat punt aan de beide kromme lijnen.
.
figuur 3 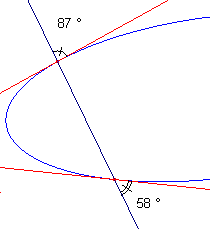loodr3

Nb.
De beide laatste definities zeggen dus iets over de hoek tussen twee objecten in een bepaald snijpunt. In een ander snijpunt kan de hoek dus een andere waarde hebben (zie figuur 3).

2. Loodrecht snijdende cirkels

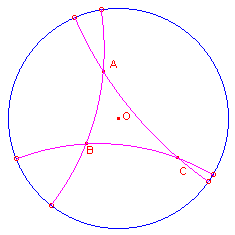
Opdracht 1
Gegeven is een cirkel met middelpunt O. Op deze cirkel ligt een punt A.
a.   Construeer een cirkel die de gegeven cirkel in A loodrecht snijdt.
Aanwijzing
De te construeren cirkel heeft de lijn OA als raaklijn.
b. Hoeveel cirkels door A zijn er die de gegeven cirkel in A loodrecht snijden?
c. Kies een tweede punt B op cirkel O.
Construeer een cirkel die gaat door A en B en die de gegeven cirkel loodrecht snijdt in A.
d. Hoeveel van dergelijke cirkels zijn er?
.
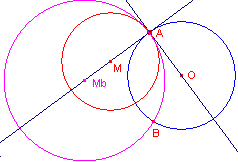figuur 4 loodr4
Opdracht 1 Ophalen van de figuur in Cabri Geometry       Animatie Animatie met CabriJava      (*)
.
(*) Voor het ophalen van de figuur in Cabri Geometry is het noodzakelijk dat Cabri II is geïnstalleerd op het gebruikte computersysteem, waarbij de Map-opties voor "Cabri-géomètre II Figure" en "Cabri-géomètre II Macro" op de juiste wijze zijn ingesteld.
Voor animaties met CabriJava moet de gebruikte browser in staat zijn Java-applicaties uit te voeren.
Is dit niet het geval, dan kunnen de figuren ook worden gedownload via deze website (zie hiervoor Download).

Opdracht 2
De constructie in Opdracht 1c kan worden uitgevoerd met behulp van het begrip "meetkundige plaats".
De gezochte cirkel heeft namelijk twee eigenschappen:
A. de cirkel snijdt de gegeven cirkel loodrecht in het punt A;
B. de cirkel gaat door de punten A en B.
Vul nu de volgende beweringen aan:

a.   De meetkundige plaats van de cirkels die voldoen aan eigenschap A is … .
b. De meetkundige plaats van de cirkels die voldoen aan eigenschap B is … .

Conclusie
Het middelpunt van de gezochte cirkel is het snijpunt van de beide meetkundige plaatsen.
figuur 5 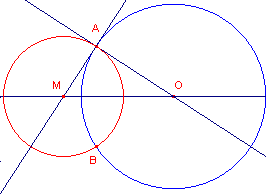loodr5
.
c.   Toon aan, dat de cirkels elkaar ook in B loodrecht snijden.
d. Ga ervan uit, dat het punt B nu niet op cirkel O ligt.
Ondergaat de constructie dan een wijziging? Geef een korte toelichting.

3. Interludium

Opdracht 3
figuur 6 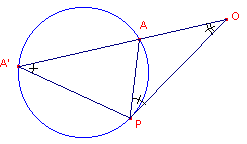loodr6 In nevenstaande figuur is OP raaklijn aan de cirkel.
A is een willekeurig punt van de cirkel.
A' is het tweede snijpunt van OA met de cirkel.
 
a. Waarom is hoek OPA gelijk aan hoek OA'P?
b. Bewijs, dat OA . OA' = OP2
Aanwijzing
Gebruik twee gelijkvormige driehoeken.

Opdracht 4
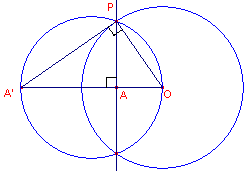figuur 7 loodr7 In nevenstaande figuur wordt de cirkel O met straal r door een tweede cirkel in het punt P loodrecht gesneden.
A is het voetpunt van P op de lijn OA'.
Bewijs, dat OA . OA' = r2.

4. Verder onderzoek
figuur 8a 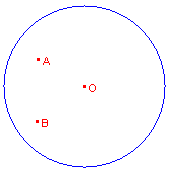loodr8 De punten A en B liggen nu beide binnen de cirkel met middelpunt O (zie figuur 8a).

Ook in dit geval willen we een cirkel construeren door A en B die de gegeven cirkel loodrecht snijdt (we doen dat in Opdracht 6).

Opdracht 5
Kijk eerst echter naar figuur 8b.
figuur 8b 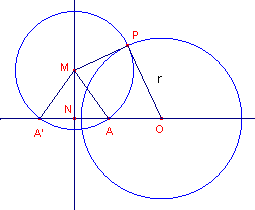loodr9 Hierin snijden de cirkels O en M elkaar loodrecht (in het punt P).
A ligt op cirkel M.
De lijn OA snijdt cirkel M verder in A'.
N is het voetpunt van M op OA.
 
a. Waarom is N het midden van AA'?
b. Als r de straal is van cirkel O, bewijs dan dat
OA . OA' = r2.
c. Op welke lijn ligt het middelpunt M van de loodrecht snijdende cirkel?

We kunnen een loodrecht snijdende cirkel door A dus construeren als we in staat zijn bij de gegeven cirkel met middelpunt O en gegeven punt A het punt A' te bepalen.
Opdracht 1 Ophalen van de figuur in Cabri Geometry       Animatie Animatie met CabriJava

Methode 1
figuur 9 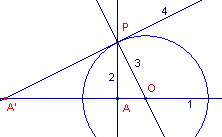loodr10
  1. Teken de lijn door O en A.
  2. Teken de loodlijn in A op OA. Het snijpunt met de cirkel is P.
  3. Teken OP.
  4. Teken de loodlijn in P op OP.
  5. Teken het punt A' als snijpunt van OA en deze loodlijn.

Methode 2, met inversie


Cabri heeft een functie waarmee het punt A' op basis van methode 1 onmiddellijk geconstrueerd kan worden.
Deze functie bevindt zich in het Afbeeldingen-menu en heeft de naam "Inversie".
  • Kies de functie Inversie in het Afbeeldingen-menu.
  • Selecteer het punt A en daarna de cirkel.

Hierna construeert Cabri het punt A'.
Dit punt wordt ook wel de inverse (het inverse punt) van A ten opzichte van de cirkel genoemd.

Opmerking


Deze constructie werkt ook als het punt A buiten de cirkel ligt. A' ligt dan binnen de cirkel.
[einde Opmerking]

5. Tenslotte
We kondigden de volgende opdracht al aan in de vorige paragraaf. In Opdracht 5 is al enig vooronderzoek met betrekking tot Opdracht 6 gepleegd.

Opdracht 6
Gegeven is een cirkel met middelpunt O.
De punten A en B liggen binnen deze cirkel (zie figuur 8a).
  • Construeer de cirkel door de punten A en B die de gegeven cirkel loodrecht snijdt.

    • Aanwijzing

    Construeer de inverse punten van A en B ten opzichte van de cirkel.

Opdracht 7, een macro (facultatief)
figuur 10 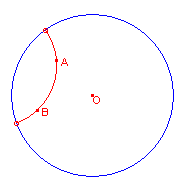loodr11 Gegeven is een cirkel met middelpunt O.
De punten A en B liggen binnen deze cirkel.
.
a.   Construeer een cirkelboog door de punten A en B waarvan de "drager" (dat is dus een cirkel) de gegeven cirkel loodrecht snijdt.
We zeggen nu ook wel dat boog AB en cirkel O elkaar loodrecht snijden.
b. Definieer een macro:d-lijn die, uitgaande van de punten A, B en de cirkel (beginobjecten), de bedoelde boog (eindobject) door A en B construeert.
c. Wat is er aan de hand met de boog als A en B op een middellijn van de cirkel liggen?
Waar ligt in dit geval het "middelpunt" van de boog?
d. Werkt de door jou gedefinieerde macro ook als de beide punten op de gegeven cirkel liggen?
Indien dat niet zo is, ga dan na waarom niet.
Probeer in dit geval de macro zo te definiëren, dat de boog ook wordt getekend als de beide punten op de cirkel liggen.
.
figuur 11

loodr12
Driehoek ABC in het Poincaré-model

 Opmerking
Bovenstaande constructie van boog AB kan worden gebruikt in het Poincaré-model van de hyperbolische meetkunde.
De naam d-lijn voor de boog geeft aan, dat de boog een lijn is op een disk (het deel van het vlak binnen de cirkel).

Voor een leerlingentekst over hyperbolische meetkunde zie bijvoorbeeld:
Moderne Wiskunde - vwo bovenbouw - B2/deel 1, pg. 211-215, Wolters-Noordhoff, Groningen, 1999.

Voor een behandeling van de hyperbolische meetkunde (volgens Poincaré) zie de pagina "Hyperbolische meetkunde" op deze website.

[einde Opmerking]
Toepassing Ophalen van de figuur in Cabri Geometry       Animatie Animatie met CabriJava

6. Download
De hierboven behandelde figuren kunnen worden gedownload via deze website.
In het bestand zijn ook de  macro's opgenomen en de figuren waarmee deze macro's zijn gedefinieerd.
Klik hier om het downloaden te starten [ZIP-bestand, 15Kb].

Van het werkblad is ook een PDF-versie beschikbaar:
pdf loodrecht.pdf [58Kb]

begin pagina

[loodrecht.htm] laatste wijziging op: 06-06-2000