Een, volgens Pappos, oud probleem: de arbelos

Overzicht  ][ Inversie | Geschiedenis | Meetkunde

0. Overzicht

1. Probleemstelling
Het volgende probleem wordt door Pappos (Pappos van Alexandrië, 290-350) reeds vermeld en het stamt volgens hem al uit ongeveer 300 vC (Egypte?).
Pappos maakt er melding van in Boek IV van zijn werk Synagoge (Collectio) waarin hij, naast zijn uitbreiding van de stelling van Pythagoras, onder andere ook het "Arbelos-probleem" ( Gr. arbhloV = schoenmakersmes) oplost, dat hieronder "in moderne zetting" is geformuleerd en wordt bewezen met inversie.

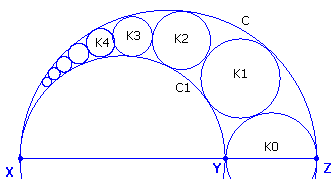
figuur  1  arbelos1 Klik hier Animatie voor een animatie van deze figuur.
 
Stelling 1
ALS
(a) X,Y, Z zijn collineair, C is de halve cirkel op XZ, C1 is de halve cirkel op XY, K0 is de halve cirkel op YZ
(b) K1, K2, ... zijn cirkels die Ki-1, C en C1 raken (zie figuur 1)
(c) straal van Kn is gelijk aan rn en d(Kn , XZ) = hn
DAN hn = 2nrn

2. Bewijs van stelling1

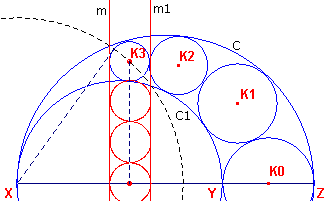figuur 2  arbelos2 Zie figuur 2.
Kies X als centrum van de inversie I en de lengte van de raaklijn uit X aan Kn als macht.
In figuur 2 is n = 3.
Dan: I(Kn) = Kn, immers de inversiecirkel en Kn snijden elkaar loodrecht.
C en C1 worden afgebeeld op rechte lijnen (X ligt op beide), waarbij I(C) = m en I(C1) = m1 beide raken aan Kn.
Voorts is m // m1 en beide loodrecht op XZ, immers I(XZ) = XZ (inversie is conform).

De cirkels K0, K1, K2, ... worden afgebeeld op cirkels (K0 op een halve cirkel) gelegen tussen m en m1, elkaar op volgend rakend.
Hierdoor hebben alle cirkels Kn' = I(Kn) een gelijke straal, nl. rn.
Voor hn geldt dan hn = 2nrn. ¨

Opmerking
In paragraaf 4 wordt aangegeven hoe de arbelos-rij (ook wel Pappos-rij genoemd) direct via inversie kan worden geconstrueerd..
[einde Opmerking]

3. Opmerkelijkheden

3.1. Secantcirkel
Het zou zeker te ver voeren het bewijs dat Pappos heeft gegeven van het bovenstaande hier te vermelden.
Echter, het "schoenmakersmes" heeft meer bijzondere eigenschappen.
We vermelden er enkele, oa. die gevonden zijn door Archimedes (287-211 vC) en die zijn vermeld in zijn Liber Assumptorum, te weten Stelling 2 (Prop. 4), Stelling 5 (Prop. 5) en een deel van Stelling 1, waarin hij voor slechts één geval de diameter van K1 berekent. Zie voor dit laatste de Opmerking bij de Berekening van de straal van K1..

Stelling 2
[1] De omtrek van de arbelos is gelijk aan de omtrek van de cirkel op XZ.
[2] De oppervlakte van de arbelos is gelijk aan de oppervlakte van de cirkel met de secant als middellijn.
Deze cirkel wordt ook wel secantcirkel genoemd. De secant is het lijnstuk PY loodrecht in Y op XZ.

Bewijs: zie figuur 3.

figuur 3  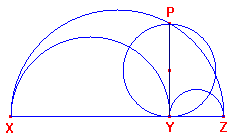arbelos3 [1]
Stellen we de diameters van de cirkels op XZ, XY, YZ opvolgend gelijk aan 1, d (d<1), 1 - d.
Omtrek onderste deel van de arbelos = ½p . d + ½p(1-d) = ½p
Omtrek(bovenste deel) = ½p . 1 = ½p
Waaruit het gestelde onmiddellijk duidelijk is. ¨

[2]
Met A bedoelen we op de oppervlaktefunctie; A(d) is de oppervlakte van een halve cirkel met middellijn d. Zodat

A(arbelos)   =  A(XZ) - A(XY) - A(YZ)
 =  1/8p(1 - d2 - (1 - d)2)
 =  1/8p(1 - d2 - 1 + 2d - d2)
 =  1/8p . 2(d - d2) = 1/4pd(1 - d)

Daar PY hoogtelijn is op de hypothenusa van de in P rechthoekige driehoek XZP, geldt
PY2 = XY .YZ = d . (1 - d)
Dus A(PY) = p(½PY)2 = 1/4p . PY2 = 1/4pd(1 - d) ¨

Opmerkingen
[1]
De middellijn van de secantcirkel is dus gelijk aan PY = Ö( d(1 - d) ) (zie ook Stelling 5.2).
[2]
De secantcirkel snijdt de (halve) cirkels C1 (op XY) en K0 (op YZ) in twee bijzondere punten. Zie stelling 4a als Gevolg van stelling 3.
[einde Opmerkingen]

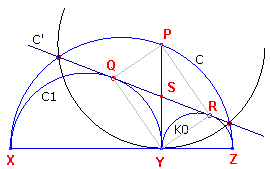
Stelling 3
De lijn door de snijpunten van de cirkel C en de cirkel met middelpunt P en straal PY raakt aan C1 en K0.

Bewijs: zie figuur 4a.

figuur 4a  arbelos4 Kiezen we de P als centrum van de inversie I en PY als inversiemacht, dan gaan C1 en K0 over in zichzelf (ze snijden de inversiecirkel loodrecht).
C gaat door het inversiecentrum en wordt dus afgebeeld op een rechte lijn C', die raakt aan (de beelden van) C1 en K0.
Hierbij is I(X) = R en I(Z) = R (raakpunten).
C' is dus gemeenschappelijk raaklijn van C1 en K0. ¨

Gevolgen
[1] Nu is eenvoudig te bewijzen, dat PQYR (zie figuur 4) een rechthoek is.
Immers, hoek XPZ is 90º, S heeft gelijke raaklijnstukken SQ = SY = SR, terwijl PS = ½QR.
Dus

Stelling 4a
De secantcirkel gaat door de raakpunten van de uitwendige raaklijn aan de beide kleinste cirkels van de arbelos.

[2]

Stelling 4b
De middellijn van de grootste cirkel die past in het segment van C bepaald door de uitwendige raaklijn en de boog door P heeft een middellijn die gelijk is aan d(1 - d). 		 

Bewijs: zie figuur 4b.

figuur 4b  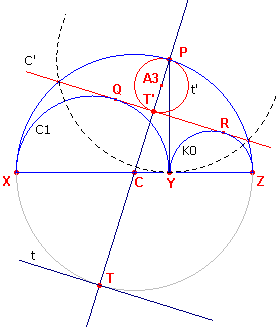arbelos4b T is het tweede snijpunt van de middellijn van C door P.
t is de raaklijn in T aan C.

Het punt T ' (het voetpunt van de loodlijn uit P op de gemeenschappelijke raaklijn) is het beeld van T bij de gebruikte inversie I.
Het beeld van de raaklijn t is dus de cirkel met middellijn PT ' (met middelpunt A3).
Dit is tevens de grootste cirkel die in het bedoelde segment van C past.
De macht van I is gelijk aan PY =  Ö( d(1 - d) ).
Nu is PT . PT ' = 1 . PT ' = PY2 = d(1 - d)
Dus PT' = d(1 - d).

Opmerking
Cirkels met een middellijn gelijk aan die van A3 komen we ook tegen in stelling 5.1.
[einde Opmerking]

[einde Gevolgen]

3.2. Twee Archimedes-cirkels

Stelling 5
[1] De ingeschreven cirkels van de semi-circulaire driehoeken XYP en ZYP hebben een gelijke middellijn, gelijk aan d(1 - d). (zie figuur 5).
Deze ingeschreven cirkels heten Archimedes-cirkels.
[2] De kleinste cirkel die beide Archimedes-cirkels omvat (uitwendig raakt) heeft een middellijn die gelijk is die van de secantcirkel,  PY = Ö( d(1 - d) ).

Bewijs:
[1] We geven allereerst een constructie van de linker Archimedes-cirkel op basis van inversie.

 figuur 5 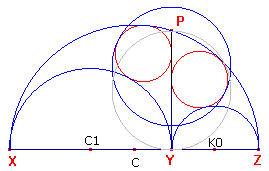arbelos5

Als inversiecentrum kiezen we het punt X, terwijl we de inversiemacht gelijk kiezen aan de lengte van XY = d.
Zie verder figuur 6.

figuur 6  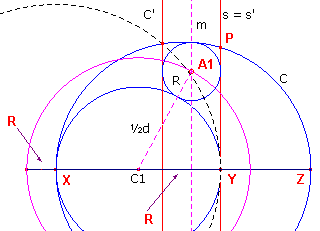arbelos6 Door de inversie gaat de cirkel C over in een rechte lijn C', terwijl de secant s overgaat in zichzelf.
De inverse van de gezochte cirkel moet nu raken aan deze beide lijnen.
Hierdoor is de straal R van de gezochte cirkel gevonden: de helft van de afstand tussen C' en s'. Het middelpunt A1 van de linker Archimedes-cirkel ligt dus op de middenparallel m van de lijnen C' en s'.
Omdat cirkel A1 ook moet raken aan cirkel C1, moet gelden C1A1 = ½d + R.
Het middelpunt kan dus gevonden worden als snijpunt van de cirkel (C1, ½d + R) en de lijn m.

We kunnen nu de gegeven constructie gebruiken om de lengte van de straal van de (linker) Archimedes-cirkel te berekenen.
Zie figuur 7.

figuur 7  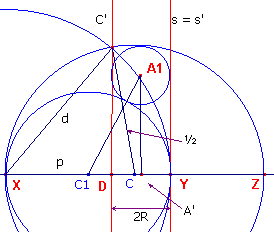arbelos7 We bepalen eerst de plaats van het punt D op XZ.
Stel XD = p. Verder is CC' = ½ en XC = ½.
In de driehoeken XDC' en CDC' passen we voor DC' de stelling van Pythagoras toe.
d2 - p2 = (½)2 - (½ - p)2
waaruit we vinden p = d2.
Dus DY = 2R = d - d2 = d(1- d)
De middellijn van de linker Archimedes-cirkel is dus gelijk aan d(1 - d).
Op dezelfde manier (of uit deze gelijkheid!) vinden we dat ook de middellijn van de rechter Archimedes-cirkel gelijk is aan  2R = d(1 - d). ¨

[2]
In driehoek C1A1A' is nu C1A1 = ½d + R   en C1A1 = ½d - R, zodat A1A'2 = d . 2R = d2(1-d).
Dus A1A'2 = h1 = dÖ(1-d)
Hieruit volgt dus voor de afstand van A2 tot de lijn XZ (zie figuur 8): h2 = (1-d)Öd.

figuur 8  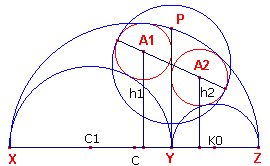arbelos8 Nu is
(h1-h2)2 = d2(1 - d) + (1 - d)2d - 2d(1 - d)Ö( d(1 - d) )
= 2Rd + 2R(1 - d) - 4RÖ(2R)
 = 2R - 4RÖ(2R)
A1A22  =  (h1 - h2)2 + 4R2
 =  2R(1 - 2Ö(2R) + 2R)
 =  2R(1 - Ö(2R) )2

De middellijn van de kleinste omgeschreven cirkel van de beide Archimedes-cirkels is dus gelijk aan
A1A2 + 2R = (1 - Ö(2R) )Ö(2R) + 2R = Ö(2R) = Ö( d(d-1) ) = PY (zie Opmerking 1 bij stelling 2). ¨

4. Constructie van de arbelos-rij

figuur 9  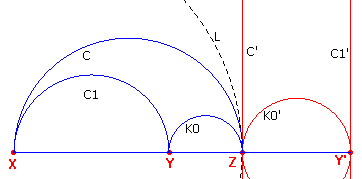arbelos9 We hebben in het bewijs in paragraaf 2 gezien, dat de arbelos-rij kan ontstaan door inversie ten opzicht van één van de exemplaren uit de rij.
We kiezen nu als inversiecirkel de cirkel L met middelpunt X en straal XZ.
De cirkel C gaat door deze inversie over in C', de loodlijn in Z op de lijn XZ.
De cirkel C1 gaat dan over in een rechte lijn C1' die gaat door het beeldpunt Y' van Y op het verlengde van XZ.

De cirkel K0 gaat nu over in de cirkel K0' waarvan het middelpunt het midden is van het lijnstuk ZY'.
De overige exemplaren van de rij kunnen dus gevonden worden als cirkels (met middellijn gelijk aan ZY') die gelegen zijn tussen C' en C1' en die elkaar opvolgend raken (zie figuur 10).

figuur 10  figuur 11
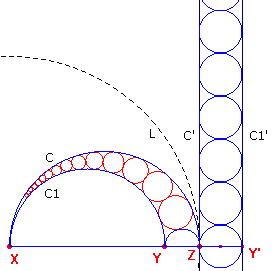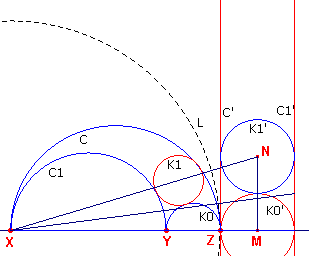arbelos10 arbelos11

Berekening van de straal r1 van K1
Op basis van de constructie van de arbelos-rij kunnen we nu de straal van K1 berekenen (zie verder figuur 11).
Zij r = ZM de straal van K0' en M, N de middelpunten van K0', K1'.
De macht m van het punt X tov. de cirkel K1' is dan m = XN2 - r2 = XM2 + MN2 - r2 = (1 + r)2 + (2r)2 - r2.
Dus
   m = 1 + 2r + 4r2
Voor de lengte van de straal van K1 hebben we dan (wegens homothetie van K1 en K1' ten opzichte van X) als vermenigvuldigingsfactor f:
   f = k2 / m (zie Inversie, paragraaf 5.2, Cirkels die niet door O gaan)
waarbij k de inversiemacht is. Wegens XZ = k = 1, is dan:
   f = 1 / m
De straal van K1 is daardoor dus gelijk aan r / (1 + 2r + 4r2)  
Wegens XY . XY ' = k2 = 1, en XY = d is XY' = 1/d en dan ZY' = 1/d - 1. Hieruit vinden we dan
  2r = (1 - d) / d
Substitutie hiervan geeft dus voor r1 =
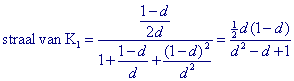
imagesarbelos_f1

Opmerking
Archimedes vermeldt in Propositie 6 van zijn Liber Asumptorum het volgende.
   Als XY = 3/2 YZ, dan is de diameter van de secant-cirkel gelijk aan 6/19 XZ.
Uit XY : YZ = 3 : 2 = d : (1-d) vinden we d = 3/5.
De middellijn van K1 is dan dus, volgens bovenstaande formule, gelijk aan imagesarbelos_f4, immers XZ = 1.
[einde Opmerking]

5. Enkele andere Archimedes-cirkels
5.1. Eén vanuit de arbelos-rij
Interessanter is het echter, op dezelfde manier als in paragraaf 4, de straal te berekenen van het beeld van de cirkel B (zie figuur 12).

figuur 12  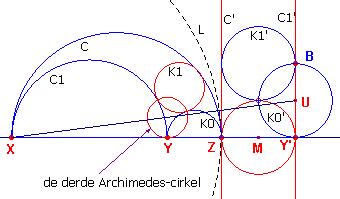arbelos12 Dit beeld gaat door de raakpunten van K1 aan C1 en K0 en door het punt Y.
Zij in dit geval m de macht van X tov. B. Dan is
m  =  XU2 - r2
 =  (1+2r)2 + r2 - r2
 =  1 + 4r + 4r2.
 =  (1 + 2r)2

In de berekening in paragraaf 4 vonden we 2r = (1 - d) / d.

De gelijkvormigheidsfactor f van B en het beeld van B is dus
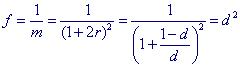
   imagesarbelos_f2
De middellijn van het beeld van B is dus gelijk aan d2 . (1 - d) / d = d(1 - d).
We hebben dus een cirkel waarvan de middellijn gelijk is aan die van de eerder behandelde Archimedes-cirkels.

Opmerking
Deze derde cirkel heet Bankoff-cirkel (naar Leon Bankoff; zie Referenties [2] )
[einde Opmerking]

Gevolg

figuur 13  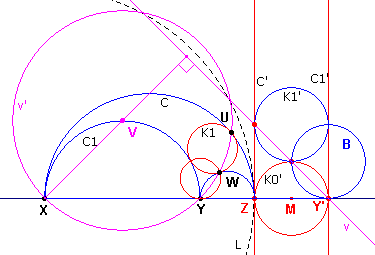arbelos13 Bekijken we nu de lijn v door de drie gemeenschappelijke punten van B, K0' en K1'.
Het beeld van deze lijn is een cirkel v' door de punten U, V, W. Maar deze cirkel gaat ook door het punt X (het centrum van de gebruikte inversie).
Stel nu afstand(X, v) = a = XY' / Ö2 = 1/(dÖ2).
De middellijn van v' is dan k2 /a (zie Inversie, Eigenschappen, Lijnen die niet door O gaan) waarin k de macht is van de inversie.
Dus middellijn v' = dÖ2.
Zij V het snijpunt van C1met de loodlijn uit X op v . Dan is
XV = d / (Ö2) = ½dÖ2.
V is dus het middelpunt van v'.

[einde Gevolg

5.2. Vier vanuit twee andere cirkels
5.2.1. De eerste twee
We tekenen de cirkels X' = (X, XY) en Z' = (Z, ZY). Deze snijden C ieder in een punt.
De kleinste cirkel door dit punt die raakt aan de secant (zie figuur 14a) is weer een cirkel waarvan de middellijn gelijk is aan d (1 - d).

figuur 14a  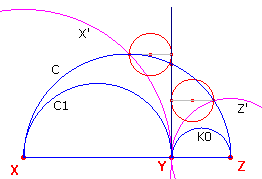arbelos14a Dit keer gebruiken we wat analytische meetkunde om de straal van beide cirkels te berekenen.
We kiezen een coördinaten stelsel met X als oorsprong en XZ als positieve x-as.
   vergelijking van C: (x - ½)2 + y2 = (½)2
   vergelijking van X': x2 + y2 = d 2
Voor de x-coördinaat van het snijpunt geldt dan
   (x - ½)2 - x2 = ¼ - d2
Dus: x = d 2
De middelijn van de cirkel links van de secant is dus gelijk aan d - d2 = d (1 - d).

   Vergelijking van Z': (x - 1)2 + y2 = (1 - d)2.
Voor de x-coördinaat van het snijpunt vinden we dan x = 2d - d2.
De middellijn van de cirkel rechts van de secant is dan (2d - d2) - d = d (1 - d).
In beide gevallen vinden we dus een straal gelijk aan die van de eerder gevonden Archimedes-cirkels.

5.2.2. Een raakcirkel van Apollonius en de vierde
We gebruiken de beide in paragraaf 5.2.1 reeds genoemde cirkels X' en Z'.
De cirkel B' die C, X', en Z' (binnen de arbelos) raakt (zie figuur 14b) is een cirkel die behoort tot geval X, A003, uit het Raakprobleem van Apollonius.

figuur 14b  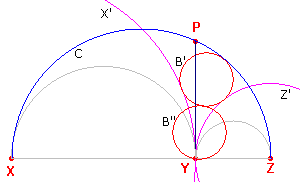arbelos14b We kunnen via de constructie van deze cirkel met behulp van inversie de diameter van deze cirkel op eenvoudige manier berekenen.
Naar zal blijken is deze diameter eveneens gelijk aan d (1 - d).

Maar, de vierde cirkel,  B", duikt dan (onmiddellijk) op. Het is de kleinste cirkel die raakt aan B' en door Y gaat. En ook van deze cirkel is de diameter gelijk aan d (1 - d).

We kiezen het punt Y als centrum van inversie en PY = k als inversiemacht. Dan is k2 = d(1-d). Zie Opmerking 1 bij stelling 2.
Bij deze inversie gaat X' over in de lijn I(X'), Z' in de lijn I(Z') en C in de cirkel I(C); zie verder figuur 15.

figuur 15  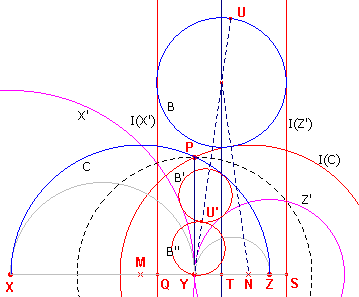arbelos15 We moeten nu de cirkel B (die het origineel is van B') construeren als uitwendig rakend aan I(C) en tevens rakend aan de lijnen I(X') en I(Z').

De macht m van het punt Y tov. de cirkel C is (afgezien van het teken) gelijk aan YX . YZ = d (1 - d).
De middellijn van de beeldcirkel I(C) is dan (wegens de vermenigvuldigingsfactor f = k2/m = 1) gelijk aan die van C; dus ook gelijk aan 1.

Uit de theorie van de inversie weten we dat de het verband tussen de middellijn l en de afstand a van het inversiecentrum tot de beeldlijn van die cirkel wordt gegeven door l = k2/a.

Hieruit volgt dan
   YQ = d(1-d) / (2d) = ½(1-d)
   YS = d(1-d) / ( 2(1-d) ) = ½d
Zodat YQ + YS = ½. De straal van de cirkel B is dus gelijk aan ¼.
Nu is YM = YN,  waarbij M en N middelpunten van de even grote cirkels C en I(C).
   YT = QT - QY = ¼ - ½(1-d) = ½d - ¼ = ½(d-½)
zodat T het midden is van YN.
Geven we het middelpunt van de cirkel B ook aan met de letter B, dan is dus YB = NB = ½ + ¼ = ¾.
De macht m van het punt Y tov. de cirkel B is dan gelijk aan YB2 - (¼)2 = ½.
De middellijn van de cirkel B' dus gelijk aan:
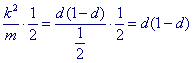
   imagesarbelos_f3
Zij U' het "eerste" snijpunt van YB met de cirkel B', en zij U het "tweede" snijpunt van YB met de cirkel B.
De punten U en U' zijn dan beeld en origineel bij de inversie.
Nu is k2 = YU' . YU = YU' . (YB+BU) = YU' . (¾ + ¼) = YU' = d (1-d).
De cirkels B' en B" hebben dus beide een middelllijn die gelijk is aan de middellijn van de Archimedes-cirkels (zie Stelling 5).

6. Referenties

[1]        Bob Allanson: "Pappus' arbelos" (website: http://members.ozemail.com.au/~llan/)
[2] Leon Bankoff: "The Marvelous Arbelos" in The Lighter Side of Mathematics (ed. R.K. Guy, R.E. Woodrow), MAAX, Washington DC, 1994
[3] Alexander Bogomolny: Arbelos - The Shoemaker's Knife (Cut-The-Knot)
[4] CRC Concise Encyclopedia of Mathematics, USA
[5] Martin Gardner: "Mathematical Games: The Diverse Pleasures of Circles that Are Tangent to One Another" in Scientific American, nr. 240, pg. 18-28, Jan. 1979
[6] Aad Goddijn: "Een ode voor de arbelos" in NieuweWiskrant, 18-4 (juni 1999), pg. 45-47, Freudenthal Instituut, Utrecht
[7] Sir Thomas L Heath: A History of Greek Mathematics, Vol. II, pg. 101-102 en 371-377, Dover Publications, Inc., New York, 1981
[8] Thomas Schoch: "My arbelos story" (website: http://www.retas.de)
Thomas Schoch: "A Dozen More Arbelos Twins" (januari 1998; eerder gepubliceerd via http://woobiola.net/)
[9] Peter Y. Woo, "The Arbelos" (website: http://woobiola.net/)
[10] Cabri-werkblad "Inversie" (op deze website)

begin pagina
[arbelos.htm] laatste wijziging op: 20-02-2006