Proposities I-44 tot en met I-48 (Pythagoras)

Overzicht  ][  Elementen  |  DK & meetkunde

Overzicht terug

  1. Inleiding
  2. Inleidende proposities
  3. De stelling van Pythagoras
  4. Wat meer over de stelling
    1. Enkele mozaiekbewijzen cabrisignal
    2. Uitbreidingen, ed.
         4.2.1. De driehoekstelling van Pappos cabrisignal
         4.2.2. Moderne bewijzen cabrisignal
         4.2.3. Concurrentie van lijnen / Stelling van Heron
         4.2.4. Uitgebreide stelling van Pythagoras
    3. Pythagoreïsche drietallen (driehoeken)
  5. Referenties

1. Inleiding terug
Het eerste Boek van de Elementen wordt besloten met enkele toepassingen van de equivalentie-theorie van oppervlakten:

De proposities I-44 en I-45 en de daarin gebruikte methode hebben vooral betekenis voor de oppervlakterekening (de "meetkundige rekenkunde" van de Grieken) die we in Boek II aantreffen.

In de volgende stellingen komt het begrip "aanpassing" voor.
Onder (bijvoorbeeld) het aanpassen van een parallelogram aan een driehoek wordt verstaan het construeren van een parallelogram waarvan de oppervlakte gelijk is aan de oppervlakte van die driehoek.

2. Inleidende proposities terug
De vertalingen uit het Grieks zijn overgenomen uit [2].

Propositie I-44 terug
Aan een gegeven rechte in een gegeven rechtlijnigen hoek een parallelogram aan te passen, gelijk aan een gegeven driehoek.

[Bedoeld is hier een parallelogram te construeren met een gegeven zijde, een gegeven hoek en een oppervlakte die gelijk is aan die van een gegeven driehoek]

Zij AB de gegeven rechte lijn, C de gegeven driehoek en D de gegeven rechtlijnige hoek.
Dan moet een parallelogram aangepast worden met de gegeven rechte lijn AB [als zijde], met een hoek die gelijk is aan de hoek D, aan de gegeven driehoek C (zie figuur 1).

figuur 1 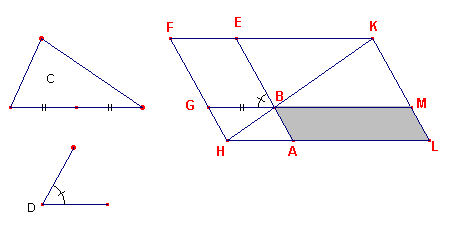imagespropI44-1

Zij het parallelogram BEFG geconstrueerd gelijk aan driehoek C, in de hoek EBG die gelijk is aan de hoek D; en laat het zo geplaatst zijn, dat BE in het verlengde ligt van AB.
Laat FG getrokken zijn door H, en laat AH getrokken zijn door A parallel met BG of BF. Laat HB verbonden zijn.

Dan, omdat de rechte lijn HF de parallellen AH, EF snijdt, zijn de hoeken AHF, HFE gelijk aan twee rechte hoeken. Dus zijn de heoken BHG, GFE minder dan twee rechte hoeken. En rechte lijnen oneindigd verlengd van hoeken die minder zijn dan twee rechte hoeken, snijden elkaar; daarom snijden HB, FE, indien verlengd, elkaar [5e postulaat].
Laat ze verlengd zijn en elkaar snijden in K; laat KL door het punt K getrokken zijn parallel met EA of FH; en laat HA, GB verlengd zijn tot de punten L, M.
Dan is HLKF een parallelogram, HK daarvan de diagonaal; en AG, ME zijn parallelogrammen, en LB, BF de zogenoemde complementen, rond HK.
Daarom is [parallelogram] LB gelijk aan [parallelogram] BF.
Maar [parallelogram] BF is gelijk aan driehoek C; dus is ook LB gelijk aan C
En omdat de hoek GBE gelijk is aan D, is ook de hoek ABM gelijk aan D.

Daarom is het parallelogram LB die gelijk isaan de gegeven driehoek C, aangepast aan de rechte lijn AB, in de hoek ABM, die gelijk is aan D.
Hetgeen gedaan moest worden. ¨

Propositie I-45 terug
In een gegeven rechtlijnigen hoek een parallelogram te construeren, gelijk aan een gegeven rechtlijnige figuur.

Zie figuur 2.

figuur 2 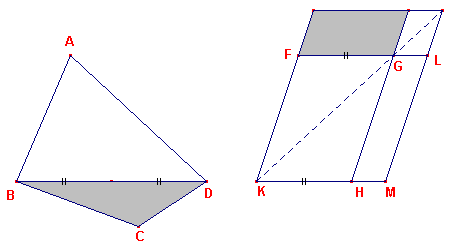imagespropI44-2

De constructie, waarbij de gegeven hoek overeenkomt met hoek HKF, wordt uitgevoerd voor het geval van een willekeurige vierhoek ABCD, waarin de diagonaal BD is getrokken
Men construeert daartoe eerst een parallelogram FH dat gelijk is aan de driehoek ABD. en past daarna propositie I-44 toe op zijde GH voor het parallelogram dat gelijk is aan driehoek BCD.
Vervolgens wordt bewezen, dat HM in het verlengde ligt van KH en dat GL in het verlengde ligt van FG, om vervolgens te bewijzen, dat KMLF het parallelogram is dat aan de gestelde eisen voldoet. ¨

Op basis van de proposities I-44 en I-45 kan men nu elk polygoon transformeren in een daarmee equivalent parallelogram met voorgeschreven hoeken en een zijde van voorgeschreven lengte.

Propositie I-46 terug
Op een gegeven rechte een vierkant te beschrijven.

Laat AB de gegeven rechte lijn zijn.
Dan moet een vierkant beschreven worden op de rechte lijn AB.

Laat AC in een rechte hoek getrokken worden op de rechte lijn AB in het punt A en laat AD gelijk gemaakt worden aan AB.
Door het punt D moet een lijn getrokken worden parallel aan AB en door het punt B moet BE getrokken worden parallel aan AD.
Dan is ADBE een parallelogram; dan is AB gelijk aan DE, en AD aan BE.
Maar AB is gelijk aan AD; dus zijn de vier rechte lijnen BA, AD, DE, EB aan elkaar gelijk.; daarom is het parallelogram ADEB gelijkzijdig.

Ik zeg vervolgens dat het ook rechthoekig is.

 figuur 3 imagespropI44-3

Want, omdat de rechte lijn AD de parallelle lijnen AB, DE snijdt, zijn de hoeken BAD, ADE gelijk aan twee rechte hoeken.
Maar de hoek BAD is recht; daarom is ook de hoek ADE recht.
En in parallel-lijnige oppervlakken zijn de overstaande zijden en hoeken aan elkaar gelijk. Daarom is elk van de overstaande hoeken ABE, BED ook recht.
Daarom is ADBE rechthoekig.
En bewezen was dat het gelijkzijdig is.
Daarom is het een vierkant; en het is beschreven op de rechte lijn AB.
Hetgeen gedaan moest worden. ¨

De bedoeling van propositie I-46 is blijkbaar een existentie-bewijs te geven voor een vierkant.
Daarvan kan dan in ieder geval gebruik gemaakt worden bij het bewijs van het beroemde theorema van Pythagoras, dat in de volgende propositie is verwoord.

3. De stelling van Pythagoras terug

Propositie I-47 terug
In rechthoekige driehoeken is het vierkant op de den rechten hoek onderspannende zijde gelijk aan de vierkanten op de den rechten hoek insluitende zijden.

Laat ABC een rechthoekige driehoek zijn met de hoek BAC recht.
Ik zeg dat het vierkant op BC gelijk is aan de vierkanten op BA, AC.

Klik hier Animatie voor een animatie van het bewijs van de stelling van Pythagoras (Pythagoras van Samos, 569-475 vC, Samos, Ionië).

Opmerking
Voor het bewijs, dat de lijnen AL, BK en CF door één punt gaan zie paragraaf 4.2 onderdeel 3.
[einde Opmerking]

figuur 4 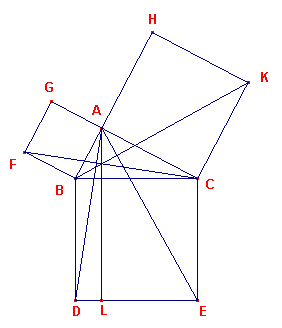imagespropI44-4 Want laat het vierkant BDEC beschreven zijn op BC, en op BA, AC de vierkanten GB, HC [propositie I-46].
Laat AL door A getrokken zijn evenwijdig met BD of CE, en laten AD, FC verbonden zijn.
Dan, omdat elk van de hoeken BAC, BAG recht is, volgt dat met een rechte lijn BA, en in punt A erop, de twee rechte lijnen AC, AG, niet liggend aan dezelfde kant, twee aanliggende hoeken maken die gelijk zijn aan twee rechte hoeken; daarom ligt CA in een rechte lijn met AG.
Om dezelfde reden ligt ook BA in een rechte lijn met AH.
En omdat de hoek DBC gelijk is aan de hek FBA, want elk is recht, laat bij elk de hoek ABC opgeteld zijn.
Daardoor is de gehele hoek DBA gelijk aan de gehele hoek FBC.
En omdat DB is gelijk aan BC, en FB aan BA, zijn de twee zijden AB, BD gelijk aan opvolgend de twee zijden FB, BC, en de hoek ABD is gelijk aan de hoek FBC. Dus de basis AD is gelijk aan de basis FC, en de driehoek ABD is gelijk aan de driehoek FBC.

Nu is het parallelogram BL het dubbele van de driehoek ABD van ze hebben dezelfde basis en liggen tussen dezelfde parallellen BD, Al.
En het vierkant GB is het dubbele van de driehoek FBC, want, ook, deze hebben dezelfde basis FB en liggen tussen dezelfde parallellen FB, GC.
Maar de dubbelen van gelijken zijn aan elkaar gelijk.
Daarom is het parallelogram BL ook gelijk aan het vierkant GB.
OP dezelfde manier, als AE, BK verbonden zijn, kan ook bewezen worden dat het parallelogram CL gelijk is aan het vierkant HC; dus het gehele vierkant BDEC is gelijk aan de twee vierkanten GB, HC, en het vierkant BDEC is beschreven op BC, en de vierkanten GB, HC op BA< AC.
Dus is het vierkant op de zijde BC gelijk aan de vierkanten op de zijden BA, AC.
Hetgeen bewezen moest worden. ¨

Opmerking
Zie ook het commentaar van Proclus bij Propositie I-47.
Zie ook de paragraaf Pythagoreïsche drietallen.
[einde Opmerking]

Propositie I-48 terug
Indien in een driehoek het vierkant op een der zijden gelijk is aan de vierkanten op de twee overige zijden van den driehoek, is de door de overige twee zijden van den driehoek ingesloten hoek recht.

Want in driehoek ABC zij het vierkant op de zijde BC gelijk aan de vierkanten op de zijden BA, AC.
Ik zeg dat de hoek BAC recht is.

Want laat AD getrokken zijn vanuit het punt A in een rechte hoek met de lijn AC, laat AD gelijk gemaakt worden aan BA, en laat CD verbonden zijn.
Omdat DA gelijk is aan AB, is het vierkant op DA gelijk aan het vierkant op AB.
Laat het vierkant op AC bij elk worden opgeteld, dan zijn de vierkanten op DA, AC gelijk aan de vierkanten op BA, AC.
Maar het vierkant op DC is gelijk aan de vierkanten op DA, AC, want de hoek DAC is recht; en het vierkant op BC is gelijk aan de vierkanten op BA, AC want dat is de hypothese.
Dus het vierkant op DC is gelijk aan het vierkant op BC, zodat de zijde DC ook gelijk is aan BC.
En omdat DA gelijk is aan AB, en AC gemeenschappelijk is, zijn de twee zijden DA, AC gelijk aan de twee zijden BA, AC. en de basis DC is gelijk aan de basis BC.		 figuur 5 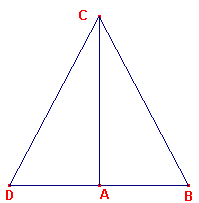imagespropI44-5

Dus de hoek DAC is gelijk aan de hoek BAC. Maar de hoek DAC is recht; daarom is de ook BAC ook recht.
Hetgeen bewezen moest worden. ¨

4. Wat meer over DE stelling terug
Er is in de loop der tijden veel gepubliceerd over de stelling van Pythagoras, met evenzo vele bewijzen.
We geven daarvan in paragraaf 4.1 enkele voorbeelden.
In paragraaf 4.2 geven we enkele uitbreidingen van de stelling voor andere figuren dan vierkanten beschreven op de zijden van een (rechthoekige) driehoek.

4.1 Enkele mozaiekbewijzen terug

[4.1.1]
In latere geschriften (eind 9e eeuw, vermoedelijk van Thãbit ibn Qurra, 836-901) wordt een bewijs gegeven, dat bekend staat als het eerste (echt zo gegeven) mozaiekbewijs (zie figuur 6).
Een voordeel van dit bewijs is, dat het de additieve equivalentie van het vierkant op de hypothenusa enerzijds en de som van de vierkanten op de beide rechthoekszijden anderzijds rechtstreeks illustreert, doordat het de laatste twee in stukken verdeelt die samen het eerste vormen.

figuur 6 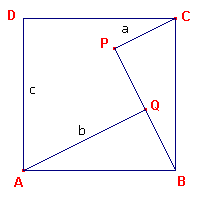imagespropI44-6 Het uitgangspunt is een vierkant met zijde c waarin twee congruente rechthoekige driehoeken zijn beschreven met rechthoekszijden a en b.
Deze beide driehoeken kunnen nu zo in de figuur geplaatst worden dat het vierkant op de zijde c uitenvalt in twee vierkanten met oppervlakten a2 en b2: rotatie van driehoek PBC om C , zodaat het beeld van B samenvalt met D en rotatie van driehoek QAB om A waarbij het beeld van B eveneens samenvalt met D

Klik hier Animatie voor een animatie van dit bewijs.

Zie ook paragraaf 4.1.5.

[4.1.2]

figuur 7 imagespropI44-7 Een mozaiek bewijs dat gebaseerd is op elementaire algebra is het volgende.
Binnen een vierkant worden op de zijden vier congruente driehoeken geplaatst (zie figuur 7). Door gebruik te maken van het bijzondere product

   (a ± b)2 = a2 ± 2ab + b2

wordt de stelling eenvoudig bewezen.

Klik hier Animatie voor een animatie van dit bewijs.

[4.1.3]

figuur 8a 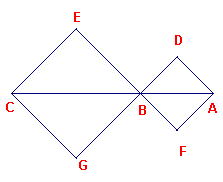imagespropI44-8a            figuur 8b 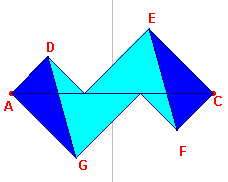imagespropI44-8b

Het in figuur 8a en figuur 8b geïllustreerde bewijs en wordt toegeschreven aan Leonardo da Vinci (1452-1519, Italië).

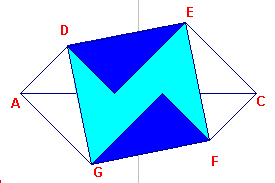figuur 8c imagespropI44-8c Het gaat uit van de vierkanten ADBF (met oppervlakte a2) en BECG (met oppervlakte b2). Door spiegeling van de van het gedeelte van de de figuur boven de lijn CA in de middelloodlijn van het lijnstuk CA gaat de figuur over de veelhoek AGFCED (zie figuur 8b). Door rotatie van de driehoeken AGD en CEF (om D resp. E) krijgen we een vierkant FEDG (zie figuur 8c) dat beschreven is op de hypothenusa van de driehoek (met oppervlakte c2).

Klik hier Animatievoor een (gedeeltelijke) animatie van het bovenstaande bewijs.

[4.1.4]

figuur 8.1  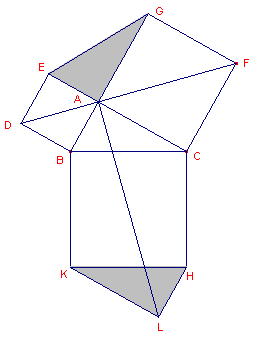propI44n1 De "Pythagoras-figuur" is aangevuld met twee driehoeken die beide congruent zijn met driehoek ABC (Tempelhof, 1769).
In de figuur is verder een viertal congruente vierhoeken te herkennen:
BDFC, DFGE en ABKL, ACHL.
De stelling volgt nu eenvoudig uit deze congruenties door weglating van de driehoeken uit de samenstellende oppervlakten.

Klik hier Animatievoor een  animatie van het bovenstaande.

[4.1.5]
Hieronder staat het vermoedelijk oudste "bewijs" van de Stelling van Pythagoras.
Het staat in het Chinese leerboek Chou-Pei Suan-Ching (ontstaan tussen 1200 en 100 vChr).

figuur 8.2 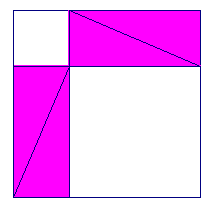propI44-82 propI44-82b Ook nu weer:
- zijde van het grootste witte vierkant = c
- zijde van het kleinste witte vierkant = a
- zijde van het derde wittevierkant = b
Dus:
   a2 + b2 = c2

Klik hier Animatievoor een  animatie met CabriJava..

[4.1.6]

figuur 8.3. 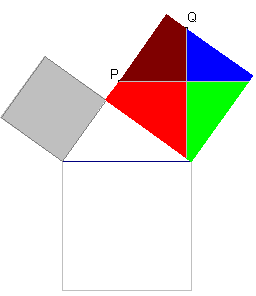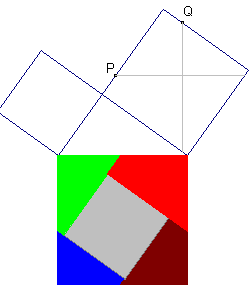propI44-83a propI44-83b In [5] en [6] vinden we een mozaïekbewijs dat afkomstig is van Henry Perigal (1801-1898, Engeland), voor het eerst gepubliceerd in 1830.
Zie ook The Messenger of Mathematics (en eventueel voor verdere links).

In dit mozaïek-bewijs wordt het vierkant op de grootste rechthoekszijde verdeeld in vierhoeken, door lijnen te trekken evenwijdig aan de zijden van het vierkant op de hypothenusa.

Klik hier Animatievoor een  animatie met CabriJava..

Zie verder [1],  [3] en [5].

4.2 Uitbreidingen, ed. terug

[4.2.1] Driehoekstelling van Pappos terug
Een van de eerste uitbreidingen van de stelling van Pythagoras is te vinden in de Synagoge (Collectio, 340) van Pappos (Pappos van Alexandrië, 290-350, Egypte - klik hier voor de wat meer bekende stelling van Pappos).
Het bijzondere hiervan is, dat de door hem gevonden eigenschap geldt voor een willekeurige driehoek.
Zeker is ook dit bewijs een fraaie toepassing van de equivalentie-theorie.

Driehoekstelling van Pappos
Als ABC een driehoek is en er zijn willekeurige parallelogrammen ABED, BCFG beschreven op AB, BC, dan zijn deze parallelogrammen gelijk aan het parallelogram ACML op AC, waarbij L op HD en M op FH ligt (met H als snijpunt van DE en FG; zie figuur 9).
figuur 9 imagespropI44-9 Bewijs:
De constructie van het parallelogram op de zijde AC verloopt als volgt.
De verlengden van DE en FG snijden elkaar in H.
De lijn HB snijdt AC in K. Door A en C worden lijnen evenwijdig met HK getrokken die opvolgend DH en FH snijden in L en M.

Nu is opp(ABED)=opp(ABHL), parallelogrammen met dezelfde basis AB en AB//DH [propositie I-35]; en
opp(BCFG)=opp(BCMH), parallelogrammen met dezelfde basis BC en BC//FH [propositie I-35].
Maar ook opp(ALHB)=opp(ALNK) en opp(CMHB)=opp(CMNK), om dezelfde reden.

Dus opp(ABED) + opp(CBGF) = opp(ALNK) + opp(CMNK) = opp(ALMC). ¨

Klik hier Animatie voor een animatie van het bewijs.

Uiteraard kan de stelling van Pythagoras als een bijzonder geval worden opgevat van de driehoekstelling van Pappos.

[4.2.2] Moderne bewijzen terug
Vandaag de dag zouden we het bewijs van de stelling van de stelling van Pythagoras wellicht leveren gebaseerd op gelijkvormigheid (zie figuur 10a).

figuur 10a 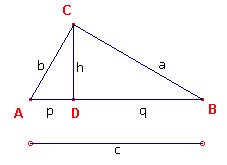imagespropI44-10 Uit de gelijkvormigheid van de driehoeken ABC en CBD volgt
AB : CB = BC : DB of c : a = a : q of a2 = cq.
Uit de gelijkvormigheid van van de driehoeken ABC en ACD volgt
AB : AC = AC : AD of c : b = b : p of b2 = cp

Optelling van beide geeft dan
a2 + b2 = cq + cp = c(q +p) = c2

Klik hier >Animatie<voor een CabriJavapplet die illustreert dat b2 = pc.

Dit bewijs zou ook door Euclides min of meer op deze wijze kunnen worden gegeven. Maar dat vereist echter kennis van de redentheorie die eerst in Boek VI wordt behandeld.

Overigens het kortste moderne bewijs maakt gebruik van vectoren (zie figuur 10b) en de daarmee samenhangende eigenschappen, zoals het inwendig product van twee vectoren (hieronder genoteerd tussen [ en ] ).:

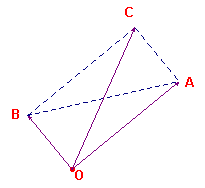imagespropI44-v      figuur 10b imagespropI44-10b

[4.2.3] Concurrentie van drie lijnen terug
In de figuur bij het bewijs van de stelling van Pythagoras, gaan de lijnen AL, BK en CF door één punt.

propI44-4 Heron van Alexandrië (10-75, Egypte) heeft (naar het schijnt) als eerste een bewijs van deze eigenschap gegeven.

Heron bewijst allereerst een drietal hulpstellingen, uiteraard gebruikmakend van de equivalentie-theorie voor oppervlakten
(zie Opmerking voor enkele andere bewijzen).
Hulpstelling 1 en 2
[1] Als, in een driehoek ABC, de lijn EF parallel aan de basis AB getrokken is, en als CD getrokken is van de top C naar het midden D van AB, dan wordt ook EF door CD in twee gelijke delen verdeeld.
[2] behandelt het geval waarin EF de verlengden van AC en BD snijdt.

Bewijs van (1): (in "moderne" notatie; zie figuur 11a)

figuur 11a 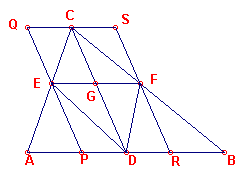imagespropI44-11 Trekken we de lijn l door C // AB, de lijn m door E // CD em de lijn n door F // CD. De snijpunten zijn P, Q, R, S.
Treek ook DE en DF.
Nu is
opp(CBD) = opp(CAD) (driehoeken op dezelfde basis, met gelijke top), en
opp(BDF) = opp(AED) (driehoken met gelijk basis en tussen dezelfde evenwijdige lijnen).

Door aftrekking van beide vinden we: opp(CFD) = opp(CED) en dus ook opp(CDRS) = opp(CDPQ) (oppervlakte van een driehoek is de helft van de oppervlakte van het parallelogram). Dus is
PD = RD (parallelogrammen tunssen dezelfde evenwijdige lijnen hebben gelijke bases). Dus ook
EG = FG. ¨

Hulpstelling 3 (omgekeerde van propositie I-43, gnomon-theorema)
Als een parallelogram AB verdeeld is de vier parallelogrammen AG, DF, FC, CE, dan ligt het gemeenschappelijk hoekpunt G op de diagonaal AB

Bewijs:

Heron verlengt AG tot het snijpunt H met CF. Dan wordt H met B verbonden. En er moet bewezen worden dat AHB een rechte lijn is.
Omdat de oppervlakten DF, EC gelijk zijn (gnomon), zijn de driehoeken DGF, ECG gelijk. Als we aan elke driehoek GCF toevoegen zijn de driehoeken ECF en DCF gelijk; en dus zijn de lijnen DE, CF parallel.
De driehoeken AEK en GDK zijn congruent en daarom is EK = KD.		 figuur 11b 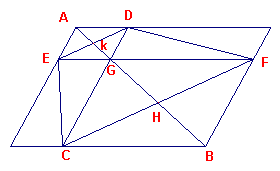imagespropI44-11b

Volgens hulpstelling 2 is dan CH = HF. In de driehoeken FHB, CHG zijn de zijden BF, FH gelijk aan de zijden GC, CH. en de hoek BFH = hoek GCH. De driehoeken zijn dus congruent, waaruit volgt dat hoek BHF = hoek GHC.
Tellen we bij beide de hoek GHF op, dan vinden we dat de hoeken BHF, FGH gelijk zijn aan de hoeken CHG, GHF. En deze laatste is een gelijk een twee rechte hoeken.
Dus is de lijn AHB een rechte lijn. ¨

Stelling van Heron terug
In het bewijs van de stelling van Pythagoras gaan de lijnen AL, BK en CF door één punt.

Bewijs: Zie figuur 12. Hierin is de lijn AKL getekend, loodrecht op BC, en verder snijdt EC de lijn AK in M.
Het punt M is verbonden met B en G. Te bewijzen is nu, dat BMG een rechte lijn is.
De oorspronkelijke figuur (zie figuur 4) is aangevuld met een aantal parallelogrammen.

figuur 12 imagespropI44-12 Voorts zijn de diagonalen OA, FH van het parallelogran FH getekend.
De driehoeken FAH, BAC zijn congruent; de hoek HFA is dus gelijk aan de hoek ABC, en daarom ook gelijk aan de hoek CAK (immers AK staat loodrecht op BC).
De diagonalen van de rechthoek FH snijden elkaar in Y; dus FY = YA en hoek HFA = hoek OAF.
De driehoeken OAF , CAK zijn dus congruent en daardoor liggen de lijnen OA en AKin elkaars verlengde.
Dus is OM de diagonaal van SQ; en daarom is de rechthoek AS gelijk aan de rechthoek AQ (gnomon-theorema).
Als we bij beide de rechthoek AM optellen, dan blijkt dat de rechthoek FM gelijk aan de rechthoek MH.
Maar omdat EC diagonaal is van het parallelogram FN, is rechthoek FM gelijk aan rechthoek MN.
Daarom is de rechhoek MG gelijk aan de rechthoek MN (gnomon-theorema)
Uit hulpstelling 3 (toegepast op BNGQ, MPNR, rechthoek MH) volgt dan, dat M op de diagonaal van BNGQ ligt.
Dus liggen B, M, G op een rechte lijn. ¨

Opmerking
[1]
Een bewijs gebaseerd op Hoektransversalen en de Stelling van Ceva verloopt eenvoudiger.
Klik hier voor zo'n bewijs.

[2]
Zie ook de pagina "Figuur van Vecten", Stelling 2 - Tussenresultaat
[einde Opmerking]

[4.2.4]  Uitgebreide Stelling van Pythagoras terug
In Boek VI van de Elementen komt de Stelling in een iets uitgebreidere (generaliseerde) vorm voor.
Daar gaat het om gelijkvormige, op dezelfde manier getekende, figuren die op de zijden van een rechthoekige driehoek.
Klik hier voor de Uitgebreide Stelling van Pythagoras.

4.3. Pythagoreïsche drietallen terug
Voor een Pythagoreïsch drietal (a, b, c) geldt (uiteraard) a2 + b2 = c2.
Proclus (411-485, Griekenland) vermeldt (in zijn commentaar op de Elementen, en wel bij het commentaar op Propositie 47, twee regels voor de vorming van deze drietallen (klik hier voor de Engelse vertaling):

"Bepaalde methoden voor de ontdekking van driehoeken van dit type zijn bekend, een die wordt toegeschreven aan Plato, en een andere aan Pythagoras.
[De laatste] gaat uit van oneven getallen Want deze neemt het gegeven oneven getal als de kleinste van de zijden om de rechte hoek en, nadat hiervan het vierkant genomen is en daarvan de eenheid is afgetrokken neemt ze de helft helft van de rest als de grootste zijde om de rechte hoek. Hier weer de eenheid aan toevoegend, maakt ze de derde zijde, de hypothenusa.
Als voorbeeld, nemende 3, nemende het vierkant, en aftrekkende 1 af van 9, geeft de methode de helft van 8, zijnde 4; dan, optellende weer 1, geeft dit 5; en een rechthoekige driehoek is gevonden met een zijde van 3, een andere 4 en een andere 5.
Maar de methode van Plato begint vanaf even getallen. Want het gegeven even getal nemende, neemt deze het als zijde om de rechte hoek en, nadat het in tweeën gedeeld is en de helft in het kwadraat is gebracht, maakt ze de hypothenusa door aan dit vierkant de eenheid toe te voegen en de andere zijde om de rechte hoek door van het vierkant de eenheid af te nemen.
Als voorbeeld, nemende 4, de methode kwadrateert de helft hiervan, oftewel 2, en dat maakt 4; dan, aftrekkende de eenheid, geeft dat 3 en optellende de eenheid geeft het 5.
Dus ze heeft dezelfde driehoek gevormd als die welke verkregen is door de andere methode."
(in vertaling van Dr. E.J. Dijksterhuis: De Elementen van Euclides)

In moderne formulering wordt de regel van Pythagoras uitgedrukt in de formule
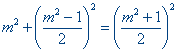
   imagesptripels1
waarin m een oneven natuurlijk getal is.

De regel van Plato luidt in formule
   imagesptripels2
waarin n een natuurlijk getal is.

In hun rekenkunde gebruikten de Pythagoreërs vaak de gnomon-configuratie (zie figuur 13).
Philoponos, die (oa.) een commentaar schreef op de Metahysica van Aristoteles, schreef:

Als een bewijs [...] refereren de Pythagoreërs aan wat er gebeurt bij de optelling van getallen; want als oneven getallen opvolgend bij elkaar worden opgeteld, blijven ze vierkant en gelijkzijdig [...]. Oneven getallen worden daarom gnomons genoemd, omdat ze, als ze worden opgeteld bij wat al vierkanten zijn, ze de vierkante vorm behouden [...]. Alexander heeft op uitstekende wijze uitgelegd, dat de zin 'als gnomons rond om geplaatst zijn' betekent 'een schema maken van getallen met oneven getallen' [...], want het is de praktijk van de Pythagoreërs dingen in schema's weer te geven."

figuur 13 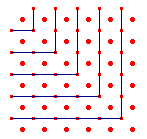imagespropI44-13 In figuur 13 is het geciteerde via een aantal gnomons in beeld gebracht.
We zien:
1 = 12
1 + 3 = 22
1 + 3 + 5 = 32
1 + 3 + 5 + 7 = 42
1 + 3 + 5 + 7 + 9 = 52
1 + 3 + 5 + 7 + 9 + 11 = 62

Op zich is het wel aardig om via gnomons ook de beide formules (die van Pythagoras en die van Plato) te illustreren (zie figuur 14a en figuur 14b).

figuur 14a - Pythagoras 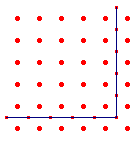imagespropI44-14a            figuur 14b - Plato 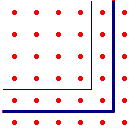imagespropI44-14b

In figuur 14a stellen we zijde van een bepaald vierkant gelijk aan a (in dit geval is dus a = 5). De gnomon erom heen telt dan dan 2a + 1 (ic. 11) eenheden. Opdat 2a + 1 zelf weer vierkant is, stellen we

 2a + 1   = n2
waardoor  a  = ½ (n2 - 1)
en dus a + 1  = ½ (n2 + 1)

Opdat hierbij a en a + 1 beide geheel zijn, moet n een oneven getal zijn.
En hieruit volgt dan eenvoudig de formule van Pythagoras.

In figuur 14b gaan we uit van een bepaald vierkant met zijde a (ic. a = 5) plus een gnomon bestaande uit rij en vergelijken met hetzelfde vierkant min een gnomon van één rij.
Voor het vierkant plus de gnomon (het grote vierkant) geldt dan
   (a + 1)2 = (a - 1)2 + 4a
Als we nu stellen, dat a = n2 dan krijgen we de formule van Plato.

Of beiden (Pythagoras en Plato) inderdaad de Pythagoreïsche drietallen via de gnomon-configuratie hebben afgeleid, is helaas onbekend.

5. Referenties terug
Op een groot aantal websites en in een bijzonder groot aantal boeken is natuurlijk geschreven over de stelling van Pythagoras en de Pythagoreïsche getallen.
We vermelden daarom slechts:

[1]     Cut-The-Knot! - op deze pagina staan 77 bewijzen
[2] DR. E.J. DIJKSTERHUIS, De Elementen van Euclides I en II, P. Noordhoff, Groningen, 1929
[3] Proclus' commentaar (op deze website)
[4] Pythagoras-links - op de website van het tijdschrift Pythagoras
[5] DR. J.H. WANSINK, Didactische oriëntatie voor wiskundeleraren, Wolters, Groningen, 1966 (deel I, pp. 224-265)
[6] H. Perigal, On geometric dissections in: The Messenger of Mathematics, 1874

begin pagina
[propI44.htm] laatste wijziging op: 15-03-2008