Boek VI

Overzicht  |  Aanpassing  |  Exces en defect  |  Gulden snede  |  Uitgebreide Stelling van Pythagoras
[  Elementen  |  Meetkunde  ]

1. Overzicht van Boek VI terug
In Boek VI wordt de redentheorie (de leer der evenredigheden) die opgezet is in Boek V, toegepast op de meetkunde.
Het boek heeft de volgende opbouw

Prop VI, 1-3 : evenredigheid van rechten
Prop VI, 4-8 : gelijkvormigheid van driehoeken
Prop VI, 9-13 : constructies
Prop VI, 14-23 : verband tussen oppervlaktentheorie en redentheorie
Prop VI, 24-30 : uitbreiding van de oppervlakterekening met behulp van de redentheorie
Prop VI, 31 : Uitgebreide Stelling van Pythagoras

De proposities 1-23 komen in sterke mate overeen met de stellingen die in de moderne planimetrie over deze onderwerpen worden behandeld. Om deze reden laten we ze op deze pagina danook weg.
Ook de overige proposities zullen we niet in extenso behandelen. Slechts die proposities die een bijzonder licht kunnen werpen op de meetkunde (in het huidige voortgezet onderwijs in Nederland) en op de algebra, worden aan de orde gesteld.

2. Aanpassing van oppervlakten terug
De Grieken pasten bij het veranderen van oppervlakten in principe een drietal operaties toe die we hieronder zullen aangeven met hyperbolische, elliptische en parabolische aanpassing van de oppervlakte.
De betekenis van die operaties vinden we eigenlijk terug in het commentaar van Proclus (411-485, GRiekenland) op de Elementen:

"Indien gij, wanneer een rechte lijn is uitgezet, het gegeven oppervlak langs de geheele rechte als zijde uitstrekt, zegt men, dat ge dat oppervlak [langs de lijn] aanpast.[paraballein] ; indien gij de lengte van het oppervlak grooter maakt dan de rechte zelf, dan zegt men dat het uitsteekt [uperballein]; indien gij haar kleiner maakt, zoodat er, wanneer het oppervlak beschreven is, iets van de rechte uitsteekt, dat het te kort schiet [elleipein]."

De meest vruchtbare toepassing van deze theorie vindt men voor het eerst in de leer der kegelsneden (Konica van Apollonios).

Ter verduidelijking vertalen we de bovenbedoelde terminologie door parabolische, hyperbolische en elliptische aanpassing. Op grond van de toepassingen die ervan bestaan, kunnen we de volgende definities geven:

De parabolische aanpassing is geheel gedefinieerd volgens en uitvoerbaar met behulp van de Proposities I, 44-45. Deze proposities leren, dat als X is een gegeven oppervlak is en a een gegeven lijnstuk, er een lijnstuk x te vinden is zodat de oppervlakte van het parallelogram op a en x gelijk is aan X, en dit alles bij een gegeven hoek j.
We zullen deze gelijkheid van oppervlakte in hetgeen volgt noteren als P(a, x) = X.

Opmerking
Denken we ons X in de vorm van een parallelogram P(m, n) met dezelfde hoek als waarin de aanpassing moet worden uitgevoerd, dan is het moderne equivalent van de parabolische aanpassing blijkbaar de constructie van het lijnstuk x, bij een gegeven lijnstuk a, waarvan de lengte voldoet aan de betrekking x = (mn) / a.
Dit is dus de constructie van de vierde evenredige.
Deze constructie kan overigens worden gebaseerd op het gnomon-theorema.

Klik hier Animatie voor een animatie van de constructie volgens het gnomon-theorema.
[einde Opmerking]

Terwijl het probleem van de parabolische aanpassing geheel bepaald is door het lijnstuk a en de hoek j, is dat niet het geval voor de beide andere aanpassingen. Hierbij eist Euclides nog een voorschift voor de vorm van het parallelogram, dat uitsteekt of te kort schiet. Bij de hyperbolische aanpassing noemen we dit het exces en bij de elliptische aanpassing het defect.
In Boek II treffen we alleen die vormen van aanpassing aan, waarin het exces of het defect een vierkant is.
Opvallend is dat Euclides nergens in Boek II een constructie geeft voor het kwadratisch exces of defect.
Toch kunnen we, zoals Simson in zijn boek The Elements of Euclid (Part 1) aannemelijk heeft gemaakt, ervan uitgaan dat de Grieken toch op basis van de theorie in Boek II hebben gewerkt.

Klik hier voor een uiteenzetting over de constructies van Simson.

3. Exces en defect terug
De behandeling van de ellipische en hyperbolische aanpassing is opgedeeld in de volgende paragrafen

3.1. Inleidende proposities
3.2. Defect
3.3. Oplossing van de vierkantsvergelijking ax - px2 = c2
3.4. Exces
3.5. Algebraïsche samenvatting

3.1. Inleidende proposities terug
Voordat Euclides verder ingaat op het exces en defect van de elliptische en hyperbolische aanpassingen van een gegeven vorm, geeft hij eerste twee proposities die een aanvulling zijn op het gnomon-theorema. We geven deze proposities zonder verder bewijs.

Propositie VI-24
In elk parallelogram zijn de parallelogrammen om de diagonaal gelijkvormig met het geheel en met elkaar
Propositie VI-26
Als van een parallelogram een parallelogram wordt afgenomen, gelijkvormig met het geheel en gelijkelijk gelegen, dat een gemeenschappelijken hoek ermee heeft, ligt het met het geheel om dezelfde diagonaal.

Tussen beide proposities in, staat de belangrijke stelling die het fundament is van de uitbreiding van de oppervlakterekening.
Overigens is niet duidelijk wat de reden hiervan is. Propositie 26 is immers onafhankelijk van propositie 25 (dit is een constructie/existentiebewijs)

Propositie VI-25
Eenzelfde [figuur] te construeeren, die gelijkvormig is met een gegeven rechtlijnige [figuur] en gelijk aan een andere gegeven rechtlijnige [figuur].

Zie figuur 1.

figuur 1 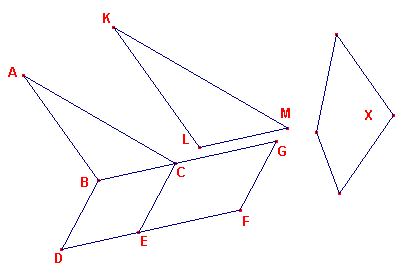imagespropVI-1 Zij ABC een driehoek waarmee de te construeren figuur gelijkvormig moet zijn.
Zij de oppervlakte van de teconstrueren figuur gelijk aan die van figuur X.

We construeren allereerst het parallelogram BE (op een willekeurige hoek) dat gelijk is aan ABC. (volgens propositie I-44).
Vervolgens construeren we op dezelfde hoek en op de zijde CE het parallelogram CF dat gelijk is aan het gegeven oppervlak X.

Als nu LM de middenevenredige is tussen BC en CG, dan kunnen we KLM gelijkvormig construeren aan ABC.

Klik hier Animatie voor een animatie die het hierna volgende bewijs van de stelling illustreert.

Bewijs:
BC : LM = LM : CG
BC : CG = parallelogram(BE) : parallelogram(CF) terwijl ook uit de redentheorie volgt
Maar (figuur op BC) : (figuur op LM) = BC : CG (*)
Hieruit volgt dan, omdat (figuur op BC) = parallelogram(BE), dat ook (figuur op LM) = parallelogram(CF) = X

(*) De Grieken beschouwden een evenredigheid niet als een getal. Daardoor kan ook niet gesproken worden over kwadraten in algebraïsche zin.
We kunnen de genoemde eigenschap echter met onze moderne middelen eenvoudig afleiden.
   ALS a : b = b : c
   DAN a2 : b2 = a2 : ac = a : c
De bedoelde eigenschap laat Euclides volgen uit (het hier niet opgenomen bewijs van) propositie VI-19 die luidt

Propositie VI-19
Gelijkvormige driehoeken staan tot elkaar in de dubbelreden van de overeenkomstige zijden

Euclides formuleert het porisma (gevolg) van deze propositie als volgt

Hieruit [uit het bewijs van de propositie; dk] is duidelijk, dat als drie lijnen evenredig zijn [a, b en c, als a : b = b : c; dk], dan als de eerste is tot de derde ook de figuur beschreven op de eerste evenredig is met de figuur die gelijkvormig beschreven is op de tweede.

3.2. Defect terug
De elliptische aanpassing met een defect van voorgeschreven vorm wordt uitgevoerd in propositie VI-28.
Deze propositie wordt echter voorafgegaan door een propostie waarin een voorwaarde nodig voor het uitvoeren van die constructie wordt geformuleerd.

Propositie VI-27
Van alle parallelogrammen aangepast aan dezelfde rechte en te kort schietend met parallelogrammen, die gelijkvormig en gelijkelijk gelegen zijn met het op de helft beschrevene, is het grootste het aan de helft aangepast, dat gelijkvormig is met het defect.

Bewijs:

figuur 2 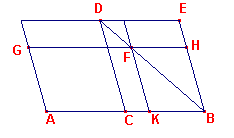imagespropVI-2 Zij AB de gegeven rechte (zie figuur 2), C het midden van AB en CBED het parallelogram van de gegeven vorm op BC.
Is nu F een willekeurig punt op BD, dan zegt de stelling dat P(AD) > P(AF).

Nu heeft het parallelogram AF (AKFG) een defect P(BF) dat gelijkvormig is met het parallelogram BD
Passen we het gnomon-theorema toe dan vinden we

AF = CG +CF = CG + FE (dit figuren, geen lijnstukken!)
Ook is AD = CG + GD = CG + DH.
Omdat DH > FE is dus ook AD > AF. ¨

Opmerking bij prop. VI-27
In moderne formulering vinden we, als we AB = a, BC / CD = p, FK = x en hoek GAB = j stellen:
CD = ½a / p en oppervlakte(AKFG) = x. Uit de verhoudingen in driehoek BCD vinden we dan, indien CK = y:
BK : BC = FK : CD of (½a - y) : ½a = x : ½a / p. Waaruit volgt dat y = ½a - px. Zodat AK = a - px.
De oppervlakte van AKFG is dus: x(a - px)sin j.
Het maximum van de uitdrukking ax - px2 vinden we nu voor x = a /2p; het maximum is dus gelijk aan a2 / 4p. En dit komt overeen met de oppervlakte van het parallelogram CBED.
[einde Opmerking]

Een afgeleide eigenschap van deze propositie is nu als voorwaarde opgenomen in

Propositie VI-28
Aan een gegeven rechte een parallelogram aan te passen, gelijk aan een gegeven rechtlijnige figuur, te kort schietend met een parallelogram gelijkvormig met een gegeven [parallelogram].
Het is dan dus nodig dat de gegeven rechtlijnige figuur niet groter is dan de figuur beschreven op de helft, gelijkvormig met het defect.

Zij AB de gegeven rechte met midden C. Zij X het gegeven oppervlak en Y de gegeven vorm van het defect (deze laatste staan niet in figuur 3).

figuur 3 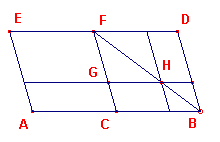imagespropVI-3 Euclides construeert eerst twee parallelogrammen ACFE en CBDF, ieder op de helft van het lijnstuk AB en ieder gelijkvormig met Y.
X mag dus niet groter zijn AF
Als X = AF dan is AF de gevraagde figuur.
Stel dus X < AF.
Euclides geeft vervolgens aan, dat er een met Y gelijkvormig parallelogram geconstrueerd moet worden waarvan de oppervlakte gelijk is aan het verschil tussen AF en X.

Deze constructie verloopt volgens propositie VI-25.
Dit parallelogram, FGHK, plaatst hij daarna in de hoek DFC van parallelogram BF.
Wegens propositieVI-26 ligt H op de diagonaal BF.
Nu is AH het gevraagde parallelogram.

Bewijs:
Nu is AH = AG + CH = BG + DH (geen lijnstukken! gnomon-theorema)
Dus is AH + FH = BG + DH + FH = BF,
terwijl ook X + FH = BF. Gevolg X = AH. ¨

3.3. Oplossing van de vierkantsvergelijking ax - px2 = c2 terug
Wanneer we ook nu weer het algebraïsche equivalent van deze constructie opschrijven, dan volgt een verrassend resultaat.

We stellen AB = a, GC = x, BC / FC = p en X = c2.
Zonder afbreuk te doen aan de constructie gaan we ervan uit, dat Y een rechthoek is
Conform de Opmerking bij propositie VI-27 moet x nu voldoen aan de vergelijking ax - px2 = c2

We kunnen nu schrijven

   px2 - ax = - c2

We tellen bij beide leden nu a2/4p op om het linker lid tot een lineaire vorm in x te make. De meetlundige betekenis van a2/4p is de oppervlakte van parallelogram BF. In het rechter lid komt dan het verschil van BF en X te staan:

   px2 - ax + a2/4p = a2/4p - c2

Deling door p geeft  

(1) ..... x2 - a/p x + a2 / 4p2 = a2 / 4p2 - c2 / p of  (x - a / 2p)2 = a2 / 4p2 - c2 / p

Om nu volgens propositie VI-25 het parallelogram FH te maken vervormen we dit verschil tot een parallelogram met basis a/2 en construeren de middenevenredige FG van de andere zijde die gelijk is aan (a2 / 4p - c2) / (a/2) en van a / 2p. We vinden dan

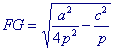imagespropVI-form1 en omdat FG = a / 2p - x vinden we dus 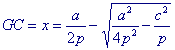imagespropVI-form2

We zien dus dat we van bovenstaande vergelijking (1) slechts één wortel vinden

Alle stappen van de meetkundige constructie kunnen we dus in de algebraïsche oplossing terugvinden.

Ook de waarwaarde voor oplosbaarheid a2 / 4p ³ c2 zien we (uiteraard) in de oplossing terug.

We missen bij Euclides de wortel x = a /2p + ÖD. De meetkudnige betekenis hiervan is dat men het parallelogram dat gelijk is aan het verschil van BF en X om het verlengde van BF construeert.
Beide oplossingen van de vergelijking zijn dus in dit geval wel terug te vinden.

3.4. Exces terug
Geheel analoog aan propositie VI-28 wordt nu behandeld

Propositie VI-29
Aan een gegeven rechte een parallelogram aan te passen, gelijk aan een gegeven rechtlijnige figuur en dat uitsteekt met een parallelogram, gelijkvormig met een gegeven [parallelogram].

Is AB weer de gegeven rechte met midden C en zij X het gegeven oppervlak en Y de gegeven vorm van het exces (deze laatste staan niet in figuur 4).

Ook nu wordt in de hoek FEC een parallelogram EG beschreven dat gelijk is aan de som van BE (het paralellelogram op het halve lijnstuk en X) en dat gelijkvormig is met Y. Op dezelfde manier als in propositie VI-28 blijkt dan, dat AG het gevraagde parallelogram is. ¨

Als we dezelfde notatie gebruiken als in paragraaf 3.3, dan is het algebraïsch equaivalent van deze constructie het oplossen van de vergelijking

   ax + px2 = c2

 figuur 4 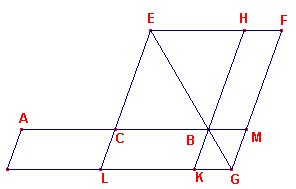imagespropVI-4

Ook hier kunnen we in de constructie weer alle stappen van de algebraïsche oplossing terugvinden.
Ditmaal is het essentieel, dat Euclides slechts één oplossing kent. Immers de vergelijking heeft nu ook een negatieve wortel. En dergelijke getallen hadden voor de Grieken geen betekenis..

3.5. Algebraïsche samenvatting terug
Beide problemen, de elliptische en de hyperbolische aanpassing, bevatten de algemene oplossing van het oplossen van een tweedegraads vergelijking.
Gaan we uit van de vergelijking

   px2 ± ax ± c2 = 0

waarin p een positief (reëel) getal is en a en c de lengtes van lijnstukken voorstellen (dus ook positief), dan zijn positieve reële oplossingen mogelijk in de volgende gevallen

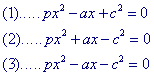
imagespropVI-form3

Geval (1) is identiek met het probleem in propositie VI-28. Het is een elliptische aanpassing aan een lijunstuk met lengte a van een oppervlak ter grootte van c2, met een defect in de vorm van een parallelogram met zijdenverhouding p.
Geval (2) is identiek met het probleem in propositie VI-29. Het is een hyperbolische aanpassing aan een lijnstuk met lengte a van een oppervlak, groot c2, met een exces in de vorm van een parallelogram eveneens met een zijdenverhouding p.
Geval (3), dat we kunnen schrijven in de vorm px2 - ax = c2, is blijkbaar eveneens een hyperbolische aanpassing aan een lijnstuk met lengte a.
Euclides behandelt dit geval niet. Het geval kan echter teruggebracht worden tot propositie VI-29.
Algebraïsch blijkt dit via de transformatie x = a/p + y, waardoor de vergelijking overgaat in py2 + ay = c2. En dit is geval (2).

figuur 5 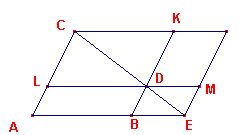imagespropVI-5 Meetkundig betekent de transformatie dat men bij een gegeven rechte AB = a het parallelogram CE met zijdenverhouding p construeert, zodat het exces KE gelijk is aan een gegeven oppervlak c2. Daarbij voert men BD als nieuwe onbekende in:
   BD = KB - KD = x - a/p
en vraagt dus naar het parallelogram AM dat gelijk is aan het gegeven oppervlak, en waarvan het exces BM de gegeven vorm heeft.

Inderdaad is nu AM = AD + BM = KM + BM = KE.

Opmerking
Indien p = 1 kunnen de bijzondere gevallen van het tweedegraadsprobleem (in dit geval hebben we een kwadratisch exces of defect) zonder gebruik te maken van de redentheorie met behulp van de oppervlakterekening van Boek II worden opgeslost.
[einde Opmerking]

4. Gulden snede - uiterste en middelste reden terug
Als toepassing van de algemene oppervlakterekening wordt nu opnieuw het probleem uit Boek II, propositie 11 gesteld, echter nu geformuleerd in de bewoordingen van de redentheorie.
Allereerst een definitie van de te gebruiken terminologie.

Definitie VI-3
Men zegt dat een rechte in uiterste en middelste reden verdeeld is, wanneer, zoals het geheel tot het grootste stuk, zoo het grootste tot het kleinste staat

en dan onmiddellijk gevolgd door

Propositie VI-30
Een gegeven begrensde rechte in uiterste en middelste reden te verdelen

Laat AB de gegeven begrensde rechte lijn zijn.
Geëist wordt AB in uiterste en middelste reden te verdelen

figuur 6 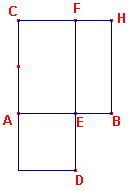imagespropVI-6 Laat op AB een vierkant beschreven zijn; en laat het parallelogram CD aangepast zijn aan AC, gelijk aan BC en met een exces AD dat gelijkvormig is met BC [volgens prop. VI-29]. Nu is BC een vierkant; daarom is ook AD een vierkant. En, omdat BC gelijk is aan CD, laat CE van beide afgetrokken worden.
Dus is de overblijvende [rechthoek] BF gelijk aan [het vierkant] AD. Maar deze zijn gelijkhoekig. Dus in BF, AD zijn de zijden rond de gelijke hoeken omgekeerd evenredig; dus zoals FE staat tot ED, is AE tot EB.
Maar FE is gelijk aan AB, en ED [is gelijk] aan AE.
Dus zoals BA staat tot AE, is AE tot EB. En AB is groter dan AE, dus is AE ook groter dan EB.

Daarom is de rechte lijn AB in uiterste en middelste reden verdeeld door E, en het grootste segment ervan is AE.
Hetgeen gedaan moest worden. ¨

Opmerkingen
[1]
Bij de uitvoering van de aanpassing volgens VI-29 moet men op de helft van AC een rechthoek constrieren die gelijk is aan de som van het vierkant op ½AC en het aan te passen oppervlak AH. Is AB = a, dan wordt de tweede zijde van die rechthoek gelijk aan 5/2a, immers a2 + 1/4a2 = 5/4a2 = 1/2a . 5/2a.
Volgens VI-25 moet men dan de middelevenredige (b) van 5/2a en 1/2a nemen en deze over 1/2a heen afpassen. We vinden dan
   b = Ö(5/4a2) = 1/2aÖ5
en
   ED = 1/2aÖ5 - 1/2a = 1/2a(Ö5 -1), een bekende uitdrukking!

Zie ook de Opmerking 3 bij propositie II-11.

[2]
Zie ook de pagina "Gulden snede en Getallen van Fibonacci".

[einde Opmerkingen]

5. Uitgebreide Stelling van Pythagoras terug
In de volgende propositie vinden we de bekende uitbreiding van de stelling van Pythagoras (prop. I-47) bij het gebruik van gelijkvormige veelhoeken op de zijden van een rechthoekige driehoek.

Propositie VI-31
In rechthoekige driehoeken is een figuur, beschreven op de den rechten hoek onderspannende zijde, gelijk aan de op de den rechten hoek omvattende zijden op gelijke wijze beschreven gelijkvormige figuren

Opmerkingen
[1]
Klik hier voor een commentaar van Proclus (411-485, Griekenland) bij Prop. I-47 en Prop. VI-31.
[2]
Klik hier voor het bewijs van Prop. VI-13 met de vertaalde tekst uit de Elementen (hieronder staat het bewijs in een "moderne" vorm).
[einde Opmerkingen]

In figuur 7 is AD loodrecht op BC. Nu is CB : BA = BA : BD.

figuur 7 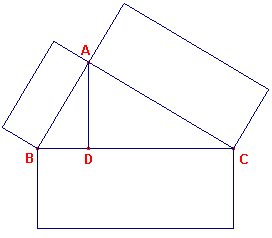imagespropVI-7 En hieruit volgt weer (zie de opmerking bij prop. VI-19)
CB : BD = opp(BC) : opp(AB),
waarin opp(PQ) betekent: de oppervlakte van de figuur beschreven op het lijnstuk PQ.
Evenzo:
CB : CD = opp(BC) : opp(AC)
waaruit we kunnen afleiden, dat
BD : opp(AB) = CD : opp(AC), of
BD : CD = opp(AB) : opp(AC).
Hieruit volgt dan het gestelde, omdat BD + CD = BC ¨

Klik hier Animatie voor een animatie van deze stelling.

[3]
Een toepassing van Prop. VI-31 is te vinden op de pagina "Maantjes van Hippocrates".

begin pagina
[propVI.htm] laatste wijziging op: 30-11-2007