Kegelsneden volgens Apollonius

Zie ook: Kegelsneden en hun vergelijkingen
Zie ook: Ellips-constructies met Cabri
Zie ook: Pooltransformaties
Zie ook: Bollen van Dandelin

1. Inleiding
Na de overwinning van Alexander de Grote op de Perzen in 333 vC ontstond een Grieks wereldrijk met Alexandrië als hoofdstad. Dit was de begintijd van het Hellenisme.
Van de geleerden uit die tijd die grote invloed op de ontwikkeling van de exacte wetenschappen hebben gehad, noemen we Euclides, Archimedes, Erathostenes en Apollonius.
Deze laatste, Apollonius van Perga (~262 - ~190 vC) studeerde in Alexandrië en ging daarna naar Pergamom, een stad die zich naast Alexandrië tot een centrum van wetenschap ontwikkelde.
Apollonius' bekendste werk is een verhandeling over kegelsneden, de zogenoemde Konika.
Uiteraard kon Apollonius zich alleen beroepen op de tot dan toe bekende methoden in de wiskunde, en deze waren eigenlijk zeer beperkt, doordat het getalbegrip bij de Grieken louter gebaseerd was op de oppervlakterekening (zie bijvoorbeeld Boek VI van de Elementen van Euclides).
In het onderstaande laten we, soms gebruikmakend van moderne methoden, zien op welke wijze Apollonius de bekende kegelsneden, ellips, hyperbool en parabool, ontwikkelde.

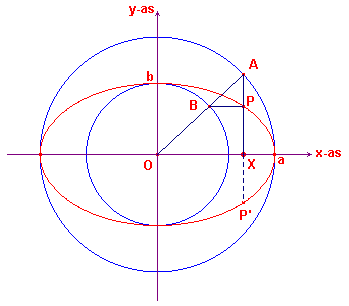
2. Verband tussen cirkel en ellips
Het verband tussen een cirkel en een ellips kan op eenvoudige wijze worden ingezien.
We laten dit verband, op basis van de vergelijkingen van beide krommen, hieronder volgen.

figuur 1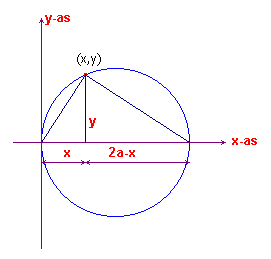

In een cartesisch coördinatenstelsel is een cirkel getekend met middellijn 2a (zie figuur 1).
Voor een punt (x, y) op deze cirkel kunnen we op eenvoudige wijze een betrekking vinden tussen de x en de y door gebruik te maken van een bekende eigenschap van de hoogtelijn op de hypothenusa:

y² = x (2a -x)

Klik hier voor een bewijs van de eigenschap van de hoogtelijn, die gebaseerd is op Propositie II-14 de Elementen van Euclides.

We kunnen nu door een transformatie (verticale lijnvermenigvuldiging) de punten van de cirkel afbeelden op de punten van een een ellips.
We vermenigvuldigen beide leden van de vergelijking met b²/a². Dit geeft, na enig rekenwerk,

( b/a y )² = (2b²/a) x - (b²/a²) x² (dit is nog steeds de vergelijking van de cirkel)

We zien in deze vergelijking, dat de y-waarde van het punt (x, y) van de cirkel vermenigvuldigd is met b/a.
Stellen we nu b/a y = y', dan is y' de y-waarde van het beeldpunt van het punt (x, y) bij de lijnvermenigvulding ten opzichte van de x-as.
Stellen we verder b²/a = p.
De vergelijking van beeldfiguur van de cirkel wordt in dit geval dus (met weglating van het accent bij de y, waarbij de x-waarde van het punt dus niet verandert):

y2 = 2p x - (p/a) x²

Dit is dus de vergelijking van de ellips (zie verder figuur 2).

figuur 2

Uit de substitutie b/a y = y' volgt de evenredigheid
   y : y' = a : b
of
   (y - y') : y = (a - b) : a
of
   AP : AX = AB : AO

Hieruit volgt dus een eenvoudige constructie van de ellips door gebruik te maken van de cirkels met middelpunt O en stralen a resp. b.

Klik hier voor een animatie van deze constructie.

Opmerkingen
[1]
Bovenstaande constructie wordt, naast enkele andere Cabri-constructies, behandeld op de pagina "Ellips-constructies met Cabri".
[2]
Op de pagina "Toegevoegde middellijnen" wordt van deze constructie eveneens gebruik gemaakt.
[einde Opmerkingen]

3. Kegelsneden: ellips - te kort schieten

figuur 3a	figuur 3b	figuur 3c
			Klik hier voor een animatie van de doorsnede van een kegel en een vlak.

Wanneer we een omwentelingskegel (hier kortweg ook kegel genoemd) snijden met een vlak ontstaat een doorsnede die we kegelsnede noemen.
Door de stand van het vlak te wijzigen krijgen we een ellips (zie figuur 3a), een parabool (zie figuur 3b) of een hyperbool (zie figuur 3c)

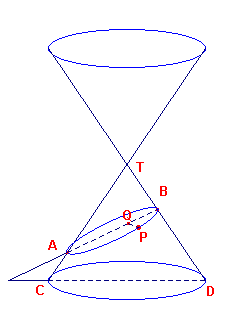
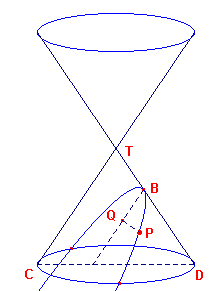
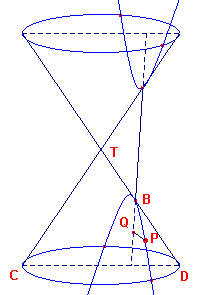
figuur 4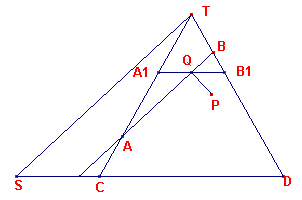

Hiernaast (in figuur 4) is de asdoorsnede TCD van een kegel getekend. De kegel wordt gesneden door een vlak V, day het vlak van tekening volgens de lijn AB snijdt (het vlak V staat dus loodrecht op het vlak van tekening).
We zullen nu op de manier waarop Apollonius dat deed, bewijzen, dat de snijfiguur F van de kegel en het vlak een ellips is.

Zij P een punt van de snijfiguur (doorsnede) F. P is in de figuur neergeklapt via de loodlijn PQ uit het punt P op AB.

Door P denken we nu een vlak dat loodrecht staat op de as van de kegel. Dit levert in de figuur de lijn A₁B₁.
Dit vlak snijdt de kegel volgens een cirkel. Voor A₁, B₁, P op deze cirkel geldt nu

PQ² = QA₁ x QB₁

De lijn TS is evenwijdig aan AB. Hierdoor ontstaan de volgende gelijkvormige driehoeken

	QA₁A en SCT	waaruit volgt QA₁ : QA = SC : ST
	QB₁B en SDT	waaruit volgt QB₁ : QB = SD : ST

Door vermenigvuldiging van deze laatste verhoudingen krijgen we de evenredigheid:

(QA₁ x QB₁) : (QA x QB) = (SC x SD) : ST²

Deze laatste verhouding, (SC x SD) : ST² = k, hangt echter alleen van de vorm van de kegel af en de stand van het vlak, en dus niet van Q en daardoor evenmin van het punt P.
Deze verhouding is dus blijkbaar geldig voor alle punten P op de doorsnede F.
Welk punt P we ook op F nemen steeds geldt dus

(QA₁ x QB₁) : (QA x QB) = k of QA₁ x QB₁ = k(QA x QB)

In verband met het eerste gevonden resultaat, PQ² = QA₁ x QB₁, vinden we dus

PQ² = k(QA x QB).

Tot zover volgen we Apollonius. Omdat onze kennis van de equivalentie-theorie en de aanpssingen van oppervlakten niet voldoende is, maken we het onderzoek naar de vorm van de doorsnede F af met een algebraïsche aanpak

We noemen nu QB = x, QP = y en AB = 2a (we kiezen dus een assenstelsel in het vlak V).

De laatste betrekking gaat dan over in

y² = k x (2a - x)

Stellen we verder, omdat a en k beide constant zijn, ak = p, dan vinden we tenslotte als vergelijking van de de doorsnede F:

y² = 2px - p/a x²

Deze vergelijking is dus dezelfde als die welke we voor de ellips gevonden hebben in paragraaf 2.

Hoewel we hier wel de methode van Apollonius hebben gevolg zijn we ten slotte toch (maar) weer naar een algebraïsche vergelijking teruggekeerd. Apollonius vatte echter de gevonden gelijkheid op in termen van oppervlakten:

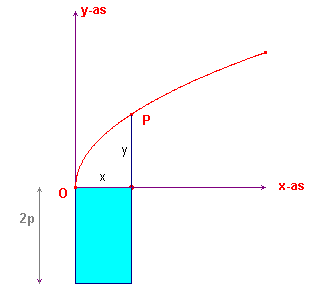
Als de vergelijking egschreven wordt als y² = x (2p - p/a x), dan zien we daaruit, dat de oppervlakte van het vierkant met zijde y gelijk is aan de oppervlakte van de rechthoek met zijden x en (x - p/a x). Deze laatste is de blauwe rechthoek in figuur 5. Het vierkant is daarin niet getekend.

figuur 5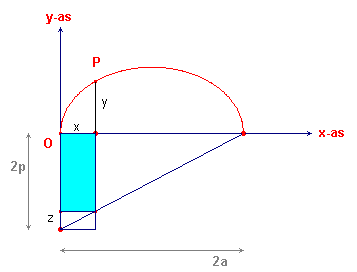

In deze figuur is 2p langs de negatieve y-as afgezet.
Door het punt (0, -2p) met het punt (2a, 0) te verbinden is een driehoek ontstaan.
Daarin geldt de volgende evenredigheid

z : x = 2p : 2a oftewel z = p/a x

De verticale zijde van de blauwe rechthoek is dus inderdaad gelijk aan 2p - z = 2p - p/a x.

De blauwe rechthoek is het verschil van de rechthoek met zijden 2p en x en de onderste (kleine) rechthoek op het lijnstuk z.

Er gaat van de rechthoek met oppervlakte 2px dus iets af.
Daarom noemde Apollonius de kromme lijn die door het punt P beschreven wordt, een ellips (van het Griekse elleiyiV, dat hier de betekenis "tekort" heeft).
Men spreekt hierom ook wel van een elliptische aanpassing van de oppervlakte.
Voor de duidelijkheid is in figuur 5 alleen de bovenste helft van de ellips getekend.

Klik hier voor een animatie van de bovenstaande "Apollonische" constructie van de ellips.

4. Hyberbool - overtreffen

figuur 6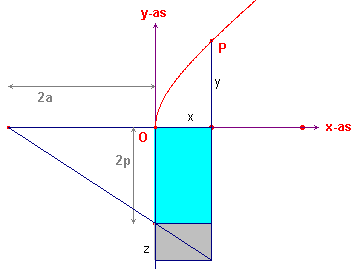

Om (het bovenste deel van de rechter tak van de) hyperbool te tekenen verbinden we (zie figuur 6) nu het punt (-2a, 0) met het punt (0, -2p). Ook nu geldt (maar nu in beide gelijkvormige rechthoekige driehoeken)

z : x = 2p : 2a en dus z = p/a x

De oppervlakte van de blauwe driehoek èn de grijze driehoek samen is nu gelijk aan x (2p + p/a x).

De vergelijking van de hyperbool luidt dus

y² = 2px + p/a x²

Er komt in dit geval dus iets bij de rechthoek met oppervlakte 2px.
Apollonius noemde de kromme lijn die door het punt P beschreven wordt, een hyperbool (van het Griekse uperbolh, dat hier de betekenis "overschot" heeft).
Men spreekt hierom ook wel van een hyperbolische aanpassing van de oppervlakte van de rechthoek.

Klik hier voor een animatie van de constructie van de hyperbool.

5. Parabool - overeenstemmen

figuur 7

We kunnen natuurlijk ook een aanpassing van het oppervlak vinden door aan de rechthoek met oppervlakte 2px niets toe te voegen.

In figuur 7 geldt dus

y² = 2px

Dit is de vergelijking van wat Apollonius een parabool noemde (van het Griekse parabolh, dat hier dus "overeenstemming" betekent).
We spreken dus hier van een parabolische aanpassing van de oppervlakte van de rechthoek.

Klik hier voor een animatie van de constructie van de parabool.

[kegelsneden.htm] laatste wijziging op: 28-12-2000