Toegevoegde middellijnen van een ellips

Overzicht  ][  Anal. meetkunde | Kegelsneden | Meetkunde

Zie ook de pagina "Kegelsneden volgens Apollonius".

0. Overzicht begin pagina

  1. Middellijnen cabrisignal
  2. Theorema's van Apollonius cabrisignal
         Eerste theorema (stelling 2)
         Tweede theorema (stelling 3)
         Gevolgen
  3. Referenties

1. Middellijnen begin pagina

Definities
[1] Een middellijn van een ellips is een lijn door het middelpunt van de ellips.
[2] Een koorde van een ellips is een verbindingslijnstuk van twee punten van de ellips.
.
Stelling 1
De meetkundige plaats van de middens van evenwijdige koorden van een ellips is (een deel van) een middellijn van die ellips
(zie figuur 1).
.
figuur 1 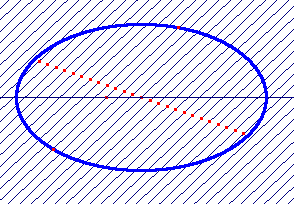midlijn1      Klik hier Animatie voor een CabriJavapplet bij figuur 1.

Bewijs: zie figuur 2.

figuur 2 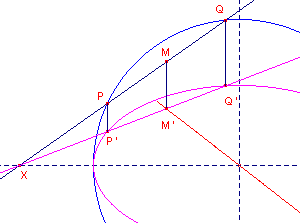midlijn2 Zijn a en b opvolgend de halve lengte van de hoofdas en de halve lengte van de nevenas van de ellips.
Door de ellips op te vatten als het beeld van de hoofdcirkel bij een verticale lijnvermenigvuldiging (*) met b/a ten opzichte van de hoofdas van de ellips, blijkt dat koorden van de cirkel overgaan in koorden van de ellips.
Bij deze afbeelding heeft het midden van een lijnstuk als beeld het midden van het beeldlijnstuk.
Het middelpunt van de cirkel is invariant.

De punten M (middens van de evenwijdige koorden van de cirkel) liggen op een rechte lijn door het middelpunt van de cirkel.
De punten M' liggen dus (ook) op een rechte lijn door het middelpunt. ¨
_____
(*) Zie de pagina "Ellips-constructies met Cabri [2]".

Gevolg
De koorden van de cirkel zijn evenwijdig met een middellijn van de cirkel. Bij de cirkel is de meetkundige plaats van de middens van de koorden de middellijn die loodrecht staat op die koorden.
Deze eigenschap geeft dus bij de ellips twee middellijnen. Elk daarvan is de verzameling van de middens van de koorden die met de andere middellijn evenwijdig zijn.

Definitie
Middellijnen met de eigenschap dat de middens van de koorden evenwijdig aan de ene middellijn liggen op de andere, heten toegevoegde middellijnen.

[einde Gevolg]

2. Theorema's van Apollonius begin pagina

Stelling 2
De som van de kwadraten van de halve lengtes van twee toegevoegde middellijnen is constant.
(Eerste Theorema van Apollonius - Apollonius van Perga, ~262 - ~190 vC)

Klik hier Animatie voor een CabriJavapplet van Stelling 2.

Bewijs: Zie figuur 3, waarin OQ1 en OQ2 toegevoegde middellijnen zijn. De lengtes van de halve assen zijn a en b.

figuur 3 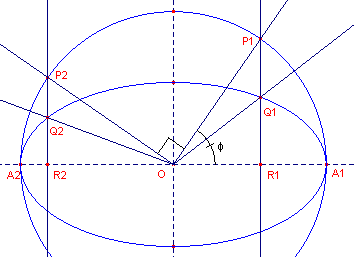midlijn3 Zij OR1 = x (dan is ook, wegens OP1 _|_ OP2, P2R2 = x).
Zij verder P1R1 = y (dus ook OR2 = y).
Wegens de verticale lijnvermenigvuldiging met b/a hebben we dan:
Q1R1 = b/a · y
En wegens sin f = y/a, is Q1R1 = bsin f.
Dus OQ12 = x2 + b2 sin2f ......(1)
Voor Q2R2 geldt: Q2R2 = b/a · x
En sin(90° - f) = cos f = x/a, zodat Q2R2 = bcos f.
Dus OQ22 = b2cos2f + y2 .......(2)
OQ12 + OQ22  =  x2 + b2sin2f + b2cos2f + y2
= x2 + y2 + b2
= a2 + b2 ¨
. begin pagina
Stelling 3
Het parallellogram op twee toegevoegde middellijnen van een ellips heeft een constante oppervlakte (= 4ab).
(Tweede Theorema van Apollonius)

Eerste bewijs: (zie figuur 4)
We bewijzen eerst dat de oppervlakte van het parallelogram op de halve toegevoegde middellijnen m1 en m2 constant is (= ab).

Klik hier Animatie voor een CabriJavapplet dat het eerste bewijs illustreert.

figuur 4 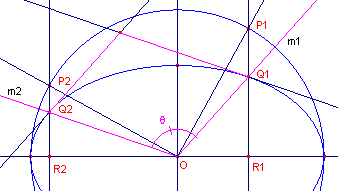midlijn4 Zij a = Ð(m1, x-as) en b = Ð(m2, x-as), en verder
   q = b - a (= Ð(m1, m2)).
Nu is
   sin q = sin b · cos a - cos b · sin a

De oppervlakte A van het bedoelde parallellogram is dan:
   A = a1b1sin q = b1sin b · a1sin a - b1cos b · a1sin a
A  =  Q2R2 · OR1 + OR2 · Q1R1
= b/a · P2R2 · x + y · b/a · P1R1
= b/a (x2 + y2) = b/a · a2 = ab

De oppervlakte van het parallellogram op de (gehele) toegevoegde middellijnen is dan dus 4ab. ¨

Klik hier Animatie voor een CabriJavapplet van deze eigenschap.

Tweede bewijs: (zie figuur 5)

figuur 5 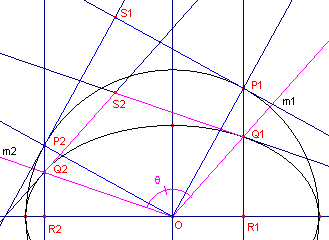midlijn5 Het parallellogram op OQ1 en OQ2 is het beeld van het vierkant op OP1 en OP2. Deze vierkanten hebben dezelfde oppervlakte. De beelden daarvan hebben bij de verticale lijnvermenigvuldiging dus ook dezelfde oppervlakte.
Omdat hiersprake is van een lijnvermenigvuldiging met factor b/a is de oppervlakte van het parallellogram dus gelijk aan
   b/a · a2 = ab. ¨

Gevolgen begin pagina

[1]   Het parallellogram op beide toegevoegde middellijnen is een omgeschreven parallellogram van de ellips (zie figuur 6).
  
[2]
Stelling 4
De meetkundige plaats van de hoekpunten der parallellogrammen beschreven op twee toegevoegde middellijnen van een ellips is een ellips, waarvan de assen samenvallen met die van de beschouwde ellips en waarvan de assen Ö2 maal zo groot zijn.

Bewijs: (zie figuur 6)

figuur 6 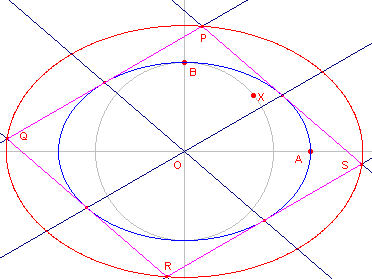midlijn6 De meetkundige plaats van de hoekpunten van vierkanten beschreven op twee loodrechte middellijnen van de hoofdcirkel is een cirkel, concentrisch met de hoofdcirkel en met straal aÖ2.
Het beeld van die cirkel bij de gebruikelijke lijnvermenigvuldiging met b/a is de bedoelde ellips. ¨

Klik hier Animatie voor een CabriJavapplet bij dit bewijs.
.
[3]
Stelling 5
Het midden M van een koorde PQ van een ellips, het snijpunt R van de raaklijnen in P en Q en het middelpunt O zijn collineair

Bewijs: (zie figuur 7)

figuur 7 midlijn7 Dit blijkt onmiddellijk uit de lijnvermenigvuldiging van de hoofdcirkel.
Immers, hierbij is collineariteit invariant.
De raaklijnen aan de cirkel gaan over in raaklijnen aan de ellips, etc. ¨

Klik hier Animatie voor een CabriJavapplet waarmee dit geïllustreerd wordt.

Opmerking. Zij OP en OQ toegevoegde middellijnen, dan is vierhoek OPRQ een parallellogram. Daaruit volgt direct dat het midden M van PQ op de lijn OR ligt (diagonalen).

[einde Gevolgen]

3. Referenties begin pagina

[1] D.J.E. SCHREK, Beknopte Analytische Meetkunde, P. Noordhoff N.V., Grongingen (1964)
[2]     J. VERSLUYS, Meetkunde der kegelsneden, A. Versluijs, Amsterdam (1909)

[middellijn.htm] Laatste wijziging op: 02-03-10 (23-12-2000)