De Elementen van Euclides

Overzicht  ][  Geschiedenis van de wiskunde | Meetkunde

---

Overzicht

1. Overzicht proposities (op deze website)
      Boek I / Boek II / Boek III / Boek VI / Boek IX
2. Inleiding
3. Opbouw
4. Boek I
5. Referenties

---

1. Overzicht proposities (op deze website)

Nb. (ruG) betekent:
Deze pagina is opgenomen ten dienste van de pagina "Meetkundige constructies" (Bètasteunpunt voor Scholieren, Rijksuniversiteit Groningen).

• Boek I
  • prop I-1 tm I-3 - cirkelconstructies (op de pagina "Passermeetkunde")
  • prop I-13 - over de gestrekte hoek (ruG)
  • prop I-16 - buitenhoek groter dan een niet-aangelegen binnenhoek
  • prop I-18 - in een driehoek onderspant de grootste zijde de grootste hoek
  • prop I-19 - in een driehoek staat de grootste hoek op de grootste zijde
  • prop I-27 - eerste stelling over evenwijdige lijnen
  • prop I-28, prop I-29, axioma van Playfair - andere stellingen over evenwijdigheid
  • prop I-32 - hoekensom en buitenhoekstelling
  • prop I-33 tm I-37 en I-43  - parallelogrammen, gnomon-theorema
  • prop I-38 - gelijke oppervlakten van driehoeken (ruG)
  • prop I-42 - constructie van een parallelogram gelijk aan een driehoek (ruG)
  • prop I-44 tm I-48 - stelling van Pythagoras, mozaiekbewijzen, driehoekstelling van Pappos,
    Pythagoreïsche drietallen 
• Boek II
  • prop II, 1-3 - optelling van oppervlakten
  • prop II, 4-7 - bijzondere algebraïsche producten, zoals (a+b)² = a² +2ab + b²
  • prop II-11 - verdeling in uiterste en middelste reden op basis van oppervlakten (gulden snede; zie ook de pagina "Gulden snede")
  • prop II-14 - oplossing van x² = ab
• Boek III
  • prop III-20 - middelpuntshoek en omtrekshoek
  • prop III-21 - hoeken op dezelfde koorde, verzameling toppen van driehoeken met gelijke basis en tophoek
  • prop III-22 - koordenvierhoek
  • prop III-31 - hoek in een halve cirkel (Thales-cirkel)
  • prop III-35 tm III-37 - machtseigenschappen bij de cirkel
• Boek VI
  • prop VI, 9-13 - constructies
  • prop VI, 25-26 - gelijkvormige parallelogrammen
  • prop VI, 27-28 - elliptische aanpassing (defect), algebraïsch equivalent daarvan
    (zie ook de pagina "Kwadratisch defect en exces volgens Simson")
  • prop VI-29 - hyperbolische aanpassing (exces)
  • algemene oplossing van een vierkantsvergelijking via de redentheorie
  • prop VI-30 - uiterste en middelste reden (gulden snede; zie ook de pagina "Gulden snede")
  • prop VI-31 - uitgebreide stelling van Pythagoras
• Boek IX
  • prop IX-20 - er zijn oneindig veel priemgetallen
  • prop IX-36 - volmaakte getallen

---

2. Inleiding
Het boek De Elementen van Euclides van Alexandrië (~325 - ~265 vC) behoort tot de mooiste en meest invloedrijke wetenschappelijke werken.
De schoonheid ervan ligt in de logische opbouw van de meetkunde en enkele ander takken van de wiskunde.
Daarnaast is het boek van grote invloed geweest op de ontwikkeling van de zogenoemde "niet-euclidische meetkunden".
Het boek is een voortdurend onderwerp van studie geweest, nu al 24 eeuwen lang, in vele talen, natuurlijk eerst in het Grieks en later als vertaling in het Arabisch, Latijn en de meeste andere moderne talen (er zijn meer dan 1000 uitgaven bekend).
De Elementen zijn talloze malen overgeschreven en van commentaar voorzien; latere schrijvers hebben er veranderingen in aangebracht waar zij dat wenselijk achtten, waardoor de oorspronkelijke tekst niet meer in alle details te reconstrueren is.
Door de logische opbouw en wijze waarop Euclides de tot dan toe bekende beginselen van de meetkunde heeft samengevat (Euclides was een uitstekend didacticus), werden de Elementen de grondslag voor het meetkunde-onderwijs tot in de twintigste eeuw.

Op deze webpagina's wordt daarom natuurlijk ook aandacht gegeven aan de Elementen, en dat niet in de laatste plaats omdat dynamische meetkunde heden ten dage weer in de belangstelling staat en via het WWW illustratieve en nieuwe didactische mogelijkheden geeft.
Deze website en in het bijzonder de pagina's die gewijd zijn aan de Elementen, zijn nog in ontwikkeling.
Het is echter niet de bedoeling om de Elementen in extenso te behandelen; er wordt veeleer een verband gelegd tussen andere op deze website aanwezige pagina's over meetkunde en de Elementen.

3. Opbouw
De inhoud van het werk voldoet aan de door Plato gestelde eis, dat de wiskunde losgemaakt dient te worden van het gebied van het materiële. Wiskundige kennis wordt volgens Plato alleen door denken verkregen. Men mag dus geen eigenschappen uit de figuur aflezen, maar men moest van elke eigenschap een streng bewijs geven en geen gebruik maken van figuren.
Volgens Aristoteles moet er bij het opbouwen van een wiskundig systeem uitgegaan worden van "algemene inzichten" die aan al het deductief denken ten grondslag liggen. Daarnaast moet gebruik gemaakt worden van "speciale inzichten", waarin de existentie van de grondbegrippen gepostuleerd en hun betekenis vastgelegd wordt. Ten slotte moet men de overige begrippen definiëren met gebruikmaking van eerdere definities en de existentie van de gedefinieerde begrippen bewijzen,

In de Elementen is Euclides er redelijk in geslaagd zich te houden aan de "voorschriften" van Plato en Aristoteles.

De Elementen bestaan uit 13 boeken.
  In de eerste 6 (Boek I tot VI) boeken wordt de planimetrie besproken.
  In Boek VII-IX wordt de rekenkunde ontwikkeld.
  Boek X gaat over rationale getallen.
  De boeken XI-XIII zijn gewijd aan de stereometrie.

4. Boek I
Boek 1 van de Elementen bevat oa. de axioma's en de postulaten waarop de "Euclidische meetkunde" is gebaseerd.

Het boek bevat

• 23 definities. Enkele daarvan zijn
  • 1. Een punt is wat geen deel heeft.
  • 2. Een lijn is een breedteloze lengte.
  • 3. De uiteinden van een lijn zijn punten.
  • 4. Een rechte lijn is een [lijn] die gelijk ligt met de punten erop.
  • 5. Een vlak is, wat alleen lengte en breedte heeft.
  • 6. De uiteinden van een vlak zijn lijnen.
  • 7. Een plat vlak is [een vlak] dat gelijk ligt met de rechte lijnen erop.
  • 15. Een cirkel is een vlakke figuur, omvat door een lijn, zodanig dat alle rechten die van éen der binnen deze figuur gelegen punten tot deze lijn neerdalen, gelijk zijn.
  • 23. Parallel zijn lijnen, die in hetzelfde platte vlak gelegen en naar weerszijden tot in het oneindige verlengd, naar geen van beide zijden elkaar ontmoeten.

  Klik hier voor de overige definities uit Boek I.

• 9 (zogenoemde) algemene inzichten, waaronder
  • 1. Dingen, gelijk aan hetzelfde, zijn ook an elkaar gelijk.
  • 2. En als men bij gelijke dingen gelijke voegt, zijn de totalen gelijk.
  • 3. En als men van gelijke dingen gelijke afneemt, zijn de resten gelijk.
  • 7. En dingen die op elkaar passen zijn gelijk.
  • 8. En het geheel is groter dan het deel.
• 5 postulaten (axioma's)
  • 1. Laat geëist zijn van elk punt naar elk [punt] een rechte lijn (een lijnstuk; DK) te trekken.
  • 2. En [laat geëist zijn] een beëindigde rechte samenhangend in een rechte lijn te verlengen (een lijnstuk verlengd tot een lijnstuk).
  • 3. En [laat geëist zijn] dat met elk middelpunt en elke afstand (bedoeld is de straal vastgelegd als een lijnstuk; DK) een cirkel beschreven wordt.
  • 4. En [laat geëist zijn] dat alle rechte hoeken aan elkaar gelijk zijn.
  • 5. En [laat geëist zijn] dat, als een rechte, die twee rechten treft, de binnenhoeken aan dezelfde kant kleiner dan twee rechte [hoeken] maakt, de twee rechten, tot in het oneindige verlengd, elkaar ontmoeten aan de kant, waar de hoeken kleiner zijn dan twee rechte [hoeken].

Opmerking
De postulaten 1-3 voldoen aan de eisen van Aristoteles. Ze postuleren de existentie van de grondbegrippen. De postulaten 4 en 5 voldoen daaraan echter niet.
In postulaat 4 wordt niet het bestaan van rechte hoeken vastgelegd, maar er wordt geëist dat we aannemen, dat alle rechte hoeken aan elkaar gelijk zijn.

figuur 1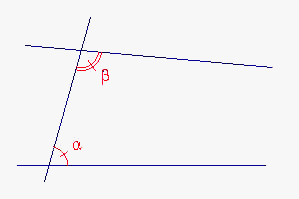

En in postulaat 5 (zie figuur 1) wordt van ons verlangd dat we aannemen, dat twee rechte lijnen die aan bepaalde voorwaarden voldoen, een snijpunt hebben. Bewezen kan worden dat postulaat 5 gelijkwaardig is met 5a. Door een punt buiten een rechte gaat precies één rechte lijn die met die rechte parallel is (axioma van Playfair)

Door wijziging van dit postulaat in

• 5h.
  Door een punt buiten een rechte gaan ten minste twee rechte lijnen die met die rechte parallel zijn
• 5e.
  Door een punt buiten een rechte gaat geen rechte lijn die met die rechte parallel is

zijn de latere niet-Euclidische meetkunden (opvolgend de "hyperbolische" en "elliptische") ontwikkeld.
[einde Opmerking]

48 proposities (stellingen), waarvan bij het bewijs in de eerste 28 en het 31e geen gebruik gemaakt wordt van het 5e postulaat.
Bijzonder is het, dat dit (dus) ook het geval is bij de proposities die betrekking hebben op conguentie van driehoeken (propositie 4, 8 en 26). Deze behouden hun geldigheid daardoor ook in de hyperbolische meetkunde.
Bij alle andere echter (29, 30 en 32-48) wordt echter wel gebruik gemaakt van het 5e postulaat.

In het bijzonder bekijken we Propositie 27 (die onafhankelijk is van het 5e postulaat)

figuur 2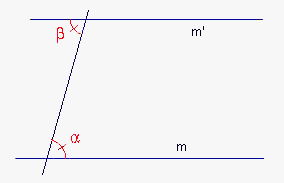

Propositie 27 Indien een rechte, twee rechten treffende, de verwisselende binnenhoeken aan elkaar gelijk maakt, zullen de rechten aan elkaar parallel zijn. Deze propositie (zie figuur 2) maakt het dus mogelijk te bewijzen dat twee lijnen parallel zijn zonder gebruik te maken van de definitie van parallelle lijnen (dus zonder ze te verlengen tot in het oneindige; zie definitie 23). Overigens is hierdoor deze stelling dus eveneens geldig in de hyperbolische meetkunde(n).

¤ Klik hier voor het bewijs van Propositie I-27 (en I-28, I-29 en het bewijs van het 5e postulaat uit het axioma van Playfair) .
¤ Klik hier voor het axioma van Wallis
¤ Zie ook de pagina "Over evenwijdige lijnen".

5. Referenties
Enkele andere websites met informatie over Euclides en de Elementen:

• Euclides van Alexandrië / met enkele afbeeldingen uit de eerste Nederlandse vertaling (W.A.W. Moll)
• Clarke University, USA (D.E. Joyce)
• Library of Congress, USA
• Yahoo, California, USA (meer links)
• University of Virginia, USA
• Simon Fraser, Canada
• Encyclopedia Britannica online
• Tufts University, USA (een electronische versie van de Elementen)
• Euclidis Beginselen der Wiskonst (website van W.A.W. Moll), eerste Nederlandse vertaling (1695)

---

[elementen.htm] laatste wijziging op: 28-10-2004