Axioma van Wallis
[ Playfair's axioma | Evenwijdige lijnen | Euclides' Elementen | Propositie I-27 ]
| Axioma Bij een gegeven (willekeurige) driehoek ABC en een gegeven lijnstuk DE bestaat een driehoek DEF (waarvan dus DE een zijde is) die gelijkvormig is met driehoek ABC. |
Op basis van dit axioma, afkomstig van John Wallis (1616-1703, Engeland) kan het 5e axioma van Euclides bewezen worden.
Het axioma van Wallis
is daarmee dus equivalent met het 5e axioma van Euclides.
We zullen deze equivalentie aantonen: door een punt P buiten een gegeven lijn m is precies één lijn is die met m evenwijdig is.
| Bewijs: | |
 |
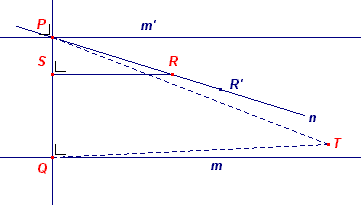Zij P dus het gegeven punt buiten de lijn m. Zij verder m' een lijn door P // m (via PQ _|_ m en m' _|_ PQ in P). Zij nu n een tweede lijn door P. We zullen nu aantonen dat de lijn n de lijn m snijdt. We kiezen, zonder de algemeenheid geweld aan te doen, een
lijn n door een punt R', waarvan de afstand tot m kleiner is dan |PQ|. |
We passen nu het axioma van Wallis toe op driehoek PRS en op lijnstuk
PQ: er is dus een punt T zo, dat PRS ~ PTQ.
We kiezen T aan dezelfde kant van PQ als R.
Uit de gelijkvormigheid volgt dan: ÐTPQ = ÐRPS.
Deze hoeken hebben de halve lijnen PQ en PS als gemeenschappelijk been.
Omdat T aan dezelfde kant van PQ ligt als R, ligt het punt T dus op n. ------(1)
Ook volgt uit de gelijkvormigheid: ÐPQT = ÐPSR,
waaruit dan (zoals hierboven) volgt, dat T op m ligt. ------(2)
Uit (1) en (2) vinden we dan, dat T het snijpunt is van m en n.
Er is dus slechts éen lijn door P evenwijdig met m. ¨
Referenties
| [1] | Cut-the-Knot: The fifth Postulate, Attempts to prove |
| [2] | MathWorld: Parallel Postulate |
| [3] | David Royster: Hyperbolic geometry / Similar Triangles (University of North Carolina, Charlotte, NC, USA) |
[wallis.htm] laatste wijziging op: 17-11-03