Over evenwijdige lijnen
Overzicht ][ Euclides' Elementen | Propositie I-27
1. Definitie en
achtergrond ![]()
De meest gebruikelijke definitie van evenwijdige lijnen (gelegen in een plat vlak) is de
volgende.
| Definitie Twee lijnen zijn evenwijdig als ze geen punt gemeenschappelijk hebben. |
Daarmee samenhagend hebben we als axioma:
| Axioma (axioma
van Playfair) Door een punt buiten een rechte gaat precies één rechte lijn die met die rechte parallel is. |
Dit axioma hangt dan weer ten nauwste samen met het 5e postulaat van Euclides:
En [laat geëist zijn] dat, als een rechte, die twee rechten treft, de binnenhoeken aan dezelfde kant kleiner dan twee rechte [hoeken] maakt, de twee rechten, tot in het oneindige verlengd, elkaar ontmoeten aan de kant, waar de hoeken kleiner zijn dan twee rechte [hoeken].
Euclides bewijst, onafhankelijk van dit postulaat:
| Propositie 27 Indien een rechte, twee rechten treffende, de verwisselende binnenhoeken aan elkaar gelijk maakt, zullen de rechten aan elkaar parallel zijn. |
Klik hier voor Euclides' bewijs van Prop.I-27.
Het is in het huidige (Nederlandse en Vlaamse) meetkundeonderwijs niet gebruikelijk om
te streven naar dergelijke bewijzen.
We geven in paragraaf 2 daarom een bewijs dat gebaseerd is op het
intuïtief aanwezige begrip rotatie, maar wel uitgaande van de hierboven
gegeven definitie.
2. Propositie 27,
anders bewezen ![]()
| Stelling 1 Twee niet-samenvallende lijnen zijn evenwijdig, als bij snijding door een derde lijn, twee overeenkomstige hoeken gelijk zijn. |
Nb.
Het is in het Nederlandse voortgezet onderwijs gebruikelijk om overeenkomstige hoeken, bij
evenwijdige lijnen gesneden door een derde, F-hoeken te noemen.
We bewijzen allereerst
| Hulpstellng 2 Overstaande hoeken zijn gelijk. |
Bewijs:
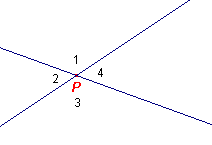 |
P1 = P12 - P2 = 180 - P2 P3 = P23 - P2 = 180 - P2 waaruit volgt dat P1 = P3 en dus ook P2 = P4. ¨ |
Bewijs van Stelling 1:
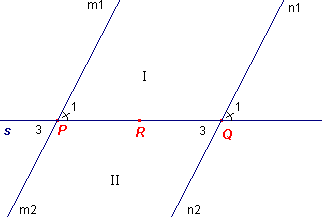 |
De snijdende lijn s deelt het vlak in twee delen die we I en II
noemen. In I liggen de halve lijnen m1 (met 'drager' m) en n1
(met 'drager' n). In II liggen de halve lijnen m2 en n2 (met 'drager' opvolgend m en n). We hebben nu: P1 = Q1 (gegeven) P1 = P3 (hulpstelling 2) zodat Q1 = P3. En ook P1 = Q1 (gegeven) Q3 = Q1 (hulpstelling 2) zodat P1 = Q3 |
We kunnen nu het vlakdeel I zo om het midden R van PQ draaien (roteren), dat hoek P1
samenvalt met hoek Q3 en hoek Q1 met P3.
Klik hier >![]() <
voor een CabriJavapplet dat deze rotatie illustreert.
<
voor een CabriJavapplet dat deze rotatie illustreert.
Dan valt m1 langs n2 en n1
langs m2.
Stel nu, dat m en n (en daardoor ook m1 en n1)
een snijpunt X zouden hebben in het vlakdeel I, dan zouden ook m2 en n2
(en dus ook m en n) een gemeenschappelijk punt Y hebben.
De lijnen m en n zouden dan twee gemeenschappelijke punten hebben.
Dit geeft echter, door gebruik te maken van een axioma (zie Opmerking 1),
noodzakelijk voor de verder opbouw van de meetkunde, dat de lijnen m en n
samenvallen.
En dit is in tegenspraak met het gegeven, dat m en n verschillend zijn.
Op dezelfde manier laten we zien, dat m en n geen snijpunt kunnen hebben
in II.
Dus m en n hebben geen punt gemeenschappelijk, en zijn dus evenwijdig (zie definitie). ¨
Opmerkingen
[1]
Het bedoelde axioma luidt:
Axioma: Door twee verschillende punten gaat precies
één rechte lijn.
[2]
Ook bij de 'intuïtieve rotatie', toegepast in het bewijs van Stelling 1,
kunnen we wat formeler te werk gaan via een axioma:
Axioma: Elke figuur kan men verplaatsen zonder
vorm- en grootteverandering.
[einde Opmerkingen]
3. Gebruik van het
axioma van Playfair ![]()
We kunnen het axioma van Playfair gebruiken om de omgekeerde stelling
van Stelling 1 te bewijzen.
| Stelling 2 Als twee evenwijdige lijnen gesneden worden door een derde, dan zijn twee overeenkomstige hoeken gelijk. |
Bewijs:
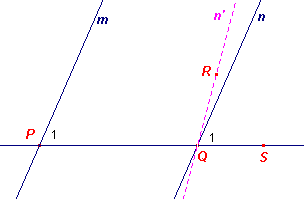 |
We willen bewijzen: ALS m // n DAN P1 = Q1 We gebruiken 'een bewijs uit het ongerijmde". We gaan uit van de ontkenning van hetgeen we willen wewijzen. Stel P1 ¹ Q1 We kunnen nu door Q een lijn n' tekenen waarbij (met R op die lijn en S op de snijdende derde lijn): RQS = P1 RQS en P1 zijn dan overeenkomstige hoeken bij snijding van m en n' door een derde lijn (QS). Dus (volgens Stelling 1): m // n' Gegeven is echter (nog steeds): m // n |
Door het punt Q gaan nu twee lijnen n en n' die evenwijdig zijn aan m.
Dit is in tegenspraak met het axioma van Playfair.
Dus dan is inderdaad P1 = Q1.
Door gebruik te maken van de gelijkheid van overstaande hoeken (zie
hulpstelling 2) kunnen we bewijzen dat andere paren overeenkomstige hoeken ook gelijk
zijn. ¨
Opmerking
Een 'bewijs uit het ongerijmde' wordt ook wel indirect bewijs
genoemd.
Bij een indirect bewijs onderstellen we dat hetgeen bewezen moet worden niet waar
is, en we tonen daarna aan, dat we daardoor in tegenspraak komen met het gegeven, met een
axima of met een eerder bewezen stelling.
[einde Opmerking]