Boek VI - constructies

Boek VI (overzicht) ][ Elementen | Meetkunde | Geschiedenis

Zie de pagina "Boek VI" voor een overzicht van de op deze website behandelde onderwerpen uit Boek VI .

Propositie VI - 9
Van een gegeven rechte een voorgeschreven deel af te nemen.

Bewijs:
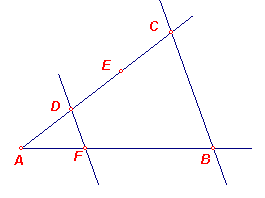	[We gebruiken hier, met Euclides, de term 'rechte' voor 'recht lijnstuk'.] De gegeven rechte is AB. Men moet van AB een gegeven deel afsnijden. Voorgeschreven is het derde deel. Men trekt vanuit A onder een willekeurige hoek met AB de lijn AC, kiest op AC een willekeurig punt D, maakt DE en EC gelijk aan AD, trekt BC en hiermee evenwijdig DEF door D. Omdat in driehoek ABC FD//BC getrokken is, geldt: CD : DA = BF : FA. Nu is CD = 2DA, dus ook BF = 2FA, en dus BA = 3AF. Dus heeft men van de gegeven rechte AB het vorgeschreven deel, namelijk AF, afgesneden. Hetgeen te construeren was. ¨
Opmerking [Uit: Dr. E.J. Dijksterhuis: De Elementen van Euclides, deel 2, pg. 91] Deze conclusie [BA = 3AF; dk] is nu echter, zooals Simson in de diep indringende kritiek (), die hij in het bijzonder op de redentheorie heeft uitgeoefend, ongeoorloofd, omdat in Boek V nergens bewezen is, dat wanneer in een evenredigheid de eerste term een veelvoud van de tweede is, de derde hetzelfde veelvoud van de vierde moet zijn, hoe vanzelfsprekend dit in de prae-Eudoxische redentheorie moet hebben geleken. __________ () Robert Simson: The Elements of Euclid (London, 1811), p. 319.

Propositie VI - 10
Een gegeven onverdeelde rechte met een gegeven verdeelde gelijkelijk te verdelen.

Bewijs:

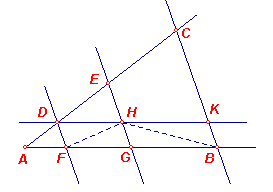Gegeven is een onverdeelde rechte AB en de door de punten D, E verdeelde rechte AC. Ze zijn zo getekend, dat ze een willekeurige hoek insluiten.
Men verbindt dan CB en trekt door D, E de met DF, EG evenwijdige lijnen, en ook DHK door D // AB.
FH en HB zijn dan parallellogrammen, dus is DH = FG, HK = GB. En daar in driehoek DKC de lijn HE // KC getrokken is, geldt
CE : ED = KH : HD
Nu is KH = BG, HD = GF, dus is ook CE : ED = BG : GF.
Evenzo is ED : DA = GF : FA omdat in driehoek AGE geldt FD // GE.
Maar hierboven is bewezen dat CE : ED = BG : GF. Dus zowel CE : ED = BG : GF als ED : DE = GF : FA.
Dus heeft men een gegeven onverdeelde rechte AB opdezelfde manier verdeeld als een gegeven verdeelde rechte AC.
Hetgeen te construeren was. ¨

Definitie V - 9
Als drie grootheden evenredig zijn, zegt men dat de eerste tot de derde de dubbelreden heeft van [haar reden] tot de tweede.

Opmerkingen
[1] We moeten hieronder voor de grootheden a, b, c (in deze volgorde) verstaan: a : b = b : c
[2] Bovenstaande definitie komt voor in het de laatste paragraaf van Deel V, en speelt verder in Deel V geen rol. Echter wel in Deel VI, en in de verdere ontwikkeling van de Griekse wiskunde.
[einde Opmerkingen]

Propositie VI - 11
Bij twee gegeven rechten een derde evenredige te vinden.

Bewijs:

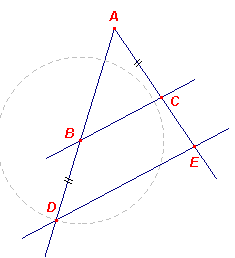De gegeven rechten zijn BA, AC die een willekeurige hoek insluiten. Men moet nu bij BA, AC de derde evenredige vinden.
Men verlengt de rechten met D, E, maakt BD = AC, trekt BC en hieraan evenwijdig DE door D.
Omdat in driehoek ADE geldt dat BC // DE, een van dezijden, geldt AB : BD = AC : CE. Nu is BD = AC, dus is
AB : AC = AC : CE
Dus heeft men bij twee gegeven rechten de derde evenredige gevonden, namelijk CE.
Hetgeen te construeren was. ¨

Propositie VI - 12
Bij drie gegeven rechten een vierde evenredige te vinden.

Bewijs:

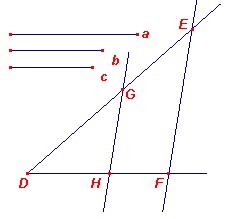De drie gegeven rechten zijn a, b, c. Men moet bij a, b, c de vierde evenredige vinden.
Men trekt twee lijnen DE, DF die een willekeurige hoek insluiten en maakt DG = a, GE = b, DH = c, trekt GH en hieraan evenwijdig EF door E.
Daar in driehoek DEF GH // EF, een van de zijden, is DG : GE = DH : EF. Nu is DG = a, GE = b, DH = c, dus is:
a : b = c : HF
Dus heeft men bij drie gegeven rechten a, b, c de vierde evenredige gevonden.
Hetgeen geconstrueerd moest worden. ¨

Propositie VI - 13
Bij twee gegeven rechten de middelevenredige te vinden.

Bewijs:

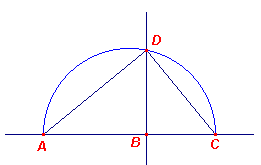De twee gegeven rechten zijn AB, BC. Men moet bij AB, BC de middelevenredige vinden.
Men heeft de rechten in elkaars verlengde gelegd. Dan tekent men de halve cirkel ADC op AC, trekt BD in B loodrecht op AC, en trekt AD, DC.
Als hoek in de halve cirkel is ADC recht [gebaseerd op de Stelling van Thales, die in Boek III voorkomt als Propositie 31]. En daar men in de rechthoekige driehoek ADC de loodlijn DB heeft op de schuine zijde, is DB middelevenredige tussen de delen AB, BC van de schuine zijde (*).
Dus heeft men bij twee gegeven rechten AB, BC de middelevenredige gevonden, namelijk DB.
Hetgeen geconstrueerd moet worden. ¨

Opmerking
De conclusie (*) is gebaseerd op Propositie VI-8 (hier niet opgenomen). Daarin wordt bewezen:

Als in een rechthoekigen driehoek uit den rechten hoek op de basis een loodlijn wordt getrokken, dan zijn de driehoeken aan de loodlijn gelijkvormig met den geheelen [driehoek] en met elkaar.

In een porisma bij deze propositie wordt dan vermeld, dat de hoogtelijn op de basis (de schuine zijde) middelevenredig is tussen de stukken waarin ze de basis verdeelt.
[einde Opmerking]

[propVIconst.htm] laatste wijziging op: 23-11-03