Proposities III-35 tot en met III-37

[ Elementen | DK & Meetkunde ]

Aan het eind van Boek III staan drie stellingen waarin de oppervlaktemeting (zie Boek II) op de cirkel wordt toegepast.
Het zijn stellingen die later aanleiding hebben gegeven tot de invoering van het begrip "macht van een punt ten opzichte van een cirkel".

De vertalingen van de proposities uit het Grieks zijn overgenomen uit:
DR. E.J. DIJKSTERHUIS, De Elementen van Euclides I en II, P. Noordhoff (Groningen, 1929)

Propositie III-35
Als in een cirkel twee rechten elkaar snijden, is de rechthoek, omvat door de deelen van de eene, gelijk aan den rechthoek omvat door de deelen van de andere.

Bewijs:

figuur 1a 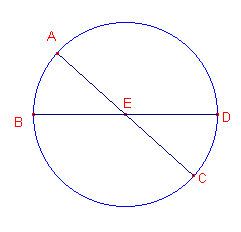propIII35-1a In een cirkel kunnen twee lijnen AC en BD elkaar snijden in een punt E.
Ik zeg nu, dat AE · EC = DE · EB.

Gaan hier AC en BD door het middelpunt van de cirkel (zie figuur 1a), zodat E het middelpunt van de cirkel is, dan is het duidelijk, dat AE, EC, DE, EB gelijk zijn, en dat ook
AE · EC = DE · EB

AC en BD kunnen ook niet door het middelpunt gaan. Zie hiervoor verder figuur 1b.
figuur 1b 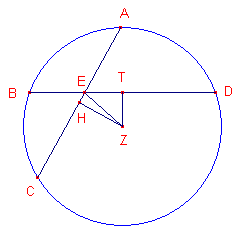propIII35-1b We tekenen de loodlijnen ZH en ZT uit het middelpunt Z op de koorden AC en BD.
Nu is volgens Prop. II-5 (en met de daar geïntroduceerde notatie):
R(AE, EC) + V(EH) = V(AH) ...... (1)
(R is hier "oppervlakte rechthoek op", V is "oppervlakte vierkant op")
Zo ook
R(BE, ED) + V(ET) = V(BT) ...... (2)
We tellen in (1) aan beide kanten van de gelijkheid V(ZH); we tellen in (2) aan beide kanten V(TZ) op. Dat geeft:
R(AE, EC) + V(EH) + V(ZH) = V(AH) + V(ZH) ...... (twee keer "stelling van Pythagoras")
R(AE, EC) + V(EZ) = V(AZ) ...... (3)
en
R(BE, ED) + V(ET) + V(TZ) = V(BT) + V(TZ) ...... (twee keer "stelling van Pythagoras")
R(BE, ED) + V(EZ) = V(BZ) ...... (4)

AZ en BZ zijn aan elkaar gelijk, dus geldt V(AZ) = V(BZ).
Uit (3) en (4) volgt dan direct het gestelde. ¨

Klik hier >Animatie< voor een CabriJavapplet bij bovenstaande propositie.

Opmerking
In de "moderne" meetkunde zouden we Prop. III-35 bewijzen met behulp van gelijkvormigheid van driehoeken (zie figuur 1c).

figuur 1c 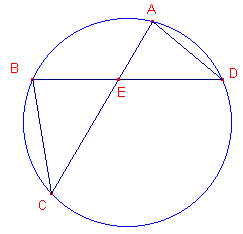propIII35c In driehoeken AED en BEC zijn:
EAD = EBC (omtrekshoeken op bg CD)
BCE = EDA (omtrekshoeken op bg AB)
Uit de gelijkvormigheid van AED en BEC volgt dan direct:
   AE : BE = ED : EC
of
   AE · EC = DE · EB

[einde Opmerking]

Propositie III-36
Als buiten een cirkel een punt genomen wordt en er dalen uit dat punt naar den cirkel twee rechten neer, en de eene daarvan snijdt den cirkel en de andere raakt hem, dan zal de [rechthoek] omvat door de heele snijdende en het buiten [den cirkel] afgesneden [stuk] tusschen punt en den bollen omtrek, gelijk zijn aan het vierkant op de rakende.

Bewijs:

figuur 2 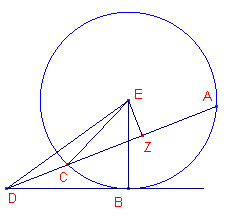propIII36 Uit het punt D zijn een snijlijn DCA en een raaklijn DB getrokken.
Nu moet bewezen worden dat: R(DA,DC) = V(DB)

Zij E het middelpunt van de cirkel.
We bewijzen alleen het geval dat de snijlijn niet door het punt E gaat.

Trek daartoe EZ loodrecht op AC; dan is Z het midden van AC.
Wegens Prop. II-6 geldt nu:

R(DA,DC) + V(ZC) = V(ZD)

Door aan beide kanten van deze identiteit V(EZ) op te tellen vinden we:
R(DA,DC) + V(ZC) + V(EZ) = V(ZD) + V(EZ)
R(DA,DC) + V(CE) = V(DE) ...... (1)

Echter, ook geldt:
V(DB) + V(EB) = V(DE), en dus: V(DB) + V(CE) = V(DE) ...... (2)
Uit (1) en (2) volgt nu het gestelde. ¨

Klik hier >Animatie< voor een CabriJavapplet bij bovenstaande propositie.

En tenslotte de omgekeerde van Prop. III-36:

Propositie III-37
Als buiten een cirkel een punt genomen wordt en er dalen uit dat punt naar den cirkel twee rechten neer en de eene daarvan snijdt den cirkel en de andere ontmoet hem (*), en wanneer de [rechthoek], omvat door de heele snijdende en het buiten [den cirkel] afgesneden [stuk] tusschen het punt en den bollen omtrek gelijk is aan het vierkant op de ontmoetende, zal de ontmoetende rechte den cirkel raken.

(*)
Dijksterhuis merkt hier op:
De letterlijke vertaling is hier niet vol te houden. De bedoeling is natuurlijk, dat van de lijn DB alleen bekend is, dat ze naar een punt van den cirkel getrokken is.

Bewijs:

figuur 3 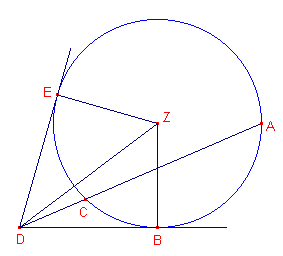propIII37 De twee bedoelde lijnen zijn: DCA en DB.
Gegeven is nu dat R(DA,DC) = V(DB) ...... (1)
Trek nu door D de (tweede) raaklijn DE aan de cirkel.
Wegens Prop. III-36 is nu:
R(DA,DC) = V(DE) ...... (2)
Uit (1) en (2) volgt dan:
V(DB) = V(DE), zodat ook DB = DE.
De driehoeken DZE en DZB hebben nu drie zijden gelijk. Volgens Prop. I-8 (niet op deze website behandeld; congruentie) volgt dan:
DBZ = DEZ = 90°
De lijn DB raakt dus aan de cirkel in het punt B.  ¨

terug
[propIII35.htm] laatste wijziging op: 02-03-03