Gulden snede en getallen van Fibonacci

Overzicht ][ Elementen | Meetkunde | Getallentheorie

Zie ook de pagina "Logaritmische spiraal".

Overzicht terug

  1. Elementen
  2. Rekenen
    2.1. Phi cabrisignal
    2.2. Verdere eigenschappen van Phi
    2.3. Constructie van een hoek van 36° cabrisignal
  3. Vijfhoek en pentagram
    3.1. Verband tussen Ö5 en de vijfhoek cabrisignal
    3.2. Het pentagram en Phi
  4. Enkele (onvermoede) vindplaatsen van Phi
    4.1. De 3-4-5-driehoek
    4.2. De macht van een punt
    4.3. Goniometrie
    4.4. Phi als kettingbreuk
    4.5. Een ring en een ellips - gulden ellips newy
  1. Gulden rechthoek en gulden driehoek
    5.1. Gulden rechthoek
    5.2. Gulden driehoek
  2. Getallen van Fibonacci
  3. Referenties

1. Elementen terug
Euclides geeft in zijn Elementen op twee plaatsen een constructie voor het verdelen van een lijnstuk in uiterste en middelste reden, ook wel het aanbengen van de gulden snede (Latijn: sectio aurea of ook wel: proportio divina) genoemd.
Hij doet dit in Boek II (propositie 11 van de "rekenkundige meetkunde") en in Boek VI (propositie 30 van de "redentheorie"); op de pagina Boek II, Opmerking 3 staat ook een 'moderne' constructie (deze constructie staat hieronder als CabriJavapplet).

In het onderstaande geven we enkele andere toepassingen van de gulden snede.

2. Rekenen terug

2.1. Phi terug
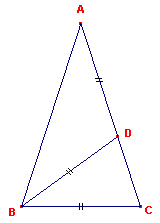
Zij C het punt dat het lijnstuk AB verdeelt in uiterste en middelste reden.
We schrijven soms wel ter afkorting: C = vumr(AB); zie figuur 1.

figuur 1 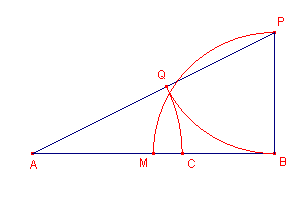sectio1 Stellen we BC = 1 en AC = x, dan is AB = x + 1.
Dan volgt uit AB : AC = AC : BC, dat
   (x + 1)/x = x / 1
zodat
(1)......   x2 - x - 1 = 0

De positieve wortel van vergelijking (1) is x = (1 + Ö5)/2.
Deze (positieve) waarde van x wordt wel aangegeven met de Griekse letter f (Phi; de eerste letter van de naam van de Griekse beeldhouwer Phidias, 490(?)-430(?) vChr).
De negatieve waarde x = (1 - Ö5)/2 geven we aan met f '.
Nu is, in vijf decimalen, f  = 1.61803 en f ' = - 0.61803 (soms wordt ook de positieve waarde 0.61803 voor f ' gebruikt).

Klik hier >Animatie< voor een CabriJavapplet van bovenstaande constructie.
o Klik hier voor een tweede constructie.

Afspraak
De verhouding AC/CB = f  heet de gulden snede.

Het grootste deel van de VUMR van AB is AC.
Nu is
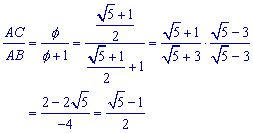
sectio1_f

In figuur 1 is ook de constructie van het punt C aangegeven.
Constructiestappen:

1 -  Midden(AB) = M    4 -  Snijpunt(2,3) = P    7 -  Snijpunt(5, 6) = Q
2 - Loodlijn(B, AB)    5 - Lijnstuk(AP)    8 - Cirkel(A, AQ)
3 - Cirkel(B, BM)    6 - Cirkel(P, PB)    9 -  Snijpunt(8, AB) = C

Bewijs:
Zij AB = a. Dan is BM = PB = ½a.
Volgens de stelling van Pythagoras in dan AP2 = a2 + ¼a2 = 5/4a2.
Nu is AQ = AC = (aÖ5)/2 - ½a = a(Ö5 - 1)/2.
Zodat
AC/AB = (Ö5-1)/2,
waaruit volgt, dat voor C geldt C = vumr(AB). ¨

2.2. Verdere eigenschappen van Phi terug
sectio2_f
Verder blijkt uit de vergelijking x2 - x - 1 = 0 en uit de berekende waarden van f en f ':
sectio3_f
(4)...... Wegens sectio4_fhebben we voorts AB =  f . AC.

2.3. Constructie van een hoek van 36° terug

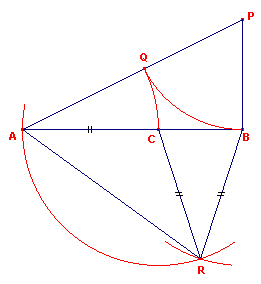figuur 2 sectio2 In figuur 2 is voortgebouwd op de constructie van figuur 1.
C = vumr(AB).
Getekend zijn opvolgend:
- Cirkel(C, CA)
- Cirkel(B, CA).
Een snijpunt van beide cirkels is het punt R.
Nu is hoek BRC = 36°. (*)

Het bewijs hiervan volgt door gebruikmaking van de eigenschap die volgt uit figuur 3.

Klik hier >Animatie< voor een CabriJavapplet van deze constructie.
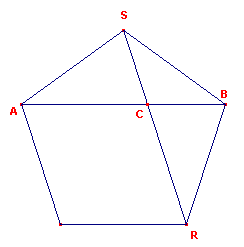figuur 3 sectio3 In de regelmatige vijfhoek in figuur 3 hebben we:
driehoek SBC ~ driehoek ABS,
waaruit:
   AB : SB = BS : BC
of ook
   AB : AC = AC : BC
Het punt C verdeelt de diagonaal AB dus in uiterste en middelste reden.
Anders geformuleerd:
.
Stelling
In een regelmatige vijfhoek verdelen snijdende diagonalen elkaar in uiterste en middelste reden.

Hieruit volgt het bewijs van de constructie van de hoek van 36° in figuur 2. ¨

(*)
Voor een afleiding van de goniometrische verhoudingen van de hoeken van 36º en 72º zie het artikel "Over de hoeken van 36º en 72º", januari 2006.
Klik hier om het artikel te downloaden (PDF-bestand; ca. 112 kB).
Opmerking. Voor het lezen van een PDF-bestand wordt Adobe Reader® geadviseerd >>> Get Reader.

3. Het pentagram terug

3.1. Verband tussen Ö5 en de vijfhoek terug
Er is een onmiskenbaar verband tussen Ö5 en f, en dus ook tussen Ö5 en de regelmatige vijfhoek.
Hieronder geven we een (en dat is één van de vele) constructie van een regelmatige vijfhoek.

figuur 3.1a 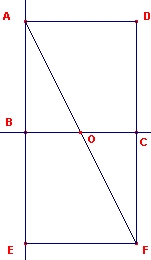sectio31a We gaan uit van een rechthoek AEFD (dubbelvierkant) met zijden 1 en 2. De lengte van de diagonaal van die rechthoek is gelijk aan Ö5 (zie figuur 3.1.a).
De lengte van het lijnstuk OA is dan dus ½Ö5.

Zie verder figuur 3.1b.

We tekenen vervolgens de cirkel (B, BC). De lengte van de straal van die cirkel is 1.
Deze cirkel is ook de omcirkel van de te construeren regelmatige vijfhoek.
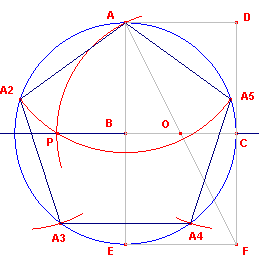figuur 3.1b sectio31b De cirkel (O, OA) snijdt de drager van het lijnstuk BC in het punt P.
De cirkel (A, AP) snijdt de omcirkel in de punten A2 en A5, samen met A hoekpunten van de regelmatige vijfhoek.
De hoekpunten A3 en A4 kunnen we vinden met de cirkels (A2, AA2) en (A5, AA2).

Klik hier >Animatie< voor een CabriJavapplet van deze constructie.

o Klik hier voor enkele andere constructies van de regelmatige vijfhoek.

3.2. Het pentagram en Phi terug

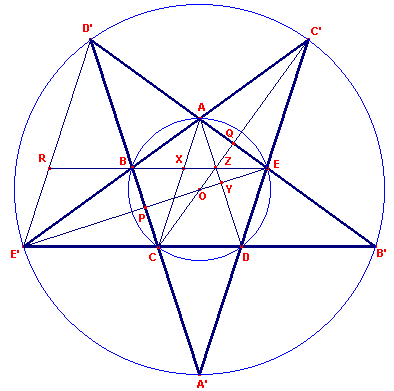figuur 4 sectio4 Het pentagram (vijfhoekige regelmatige ster) kan ontstaan door de zijden van een regelmatige vijfhoek twee aan twee te verlengen.
We kiezen AB = 1 (de zijde van de regelmatige vijfhoek).
Zijn R en r opvolgend de stralen van de omgeschreven cirkels van A'B'C'D'E' en ABCDE, dan kunnen we eenvoudig vinden:
(i)     AD' = f
(ii) OP/r = f / 2
(iii) OE'/r = f 2
(iv) OP/OE' = 2f
(v) Een diagonaal zoals BE heeft lengte f.
(vi) Is X het snijpunt van twee diagonalen AC edn BE, dan geldt:
   EX / XB = f
   CX / XA = f
(vii)     De lengtes van de lijnstukken D'B', D'E, B'A, AE, AX, XZ vormen een meetkundige rij:
   D'B' = f 3
   D'E = f 2
   B'A = f
   AE = 1
   AX = f -1
   XZ = f -2
(viii) De rij heeft ook een additieve eigenschap: de som van elk tweetal opvolgende elementen is gelijk aan het volgende element in de rij:
f + f 2 = f 3
(ix) De lengte van de zijde van A'B'C'D'E' is gelijk aan f2.
(x) R/r = f 2
(xi) De stervijfhoek en de regelmatige vijfhoek vormen de uitslag van een regelmatige vijfzijdige piramide met hoogte OE'.

4. Enkele (onvermoede) vindplaatsen van Phi terug

4.1. De 3-4-5-driehoek terug

figuur 5a 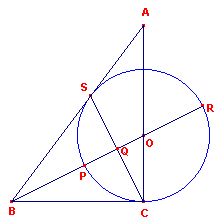sectio5 Driehoek ABC is rechthoekig in C.
AC = 4, CB = 3 en AB = 5.
De lijn door het hoekpunt B is de bissectrice van hoek B. Deze snijdt AC in het punt O.
O is het middelpunt van de cirkel door het punt C.
Omdat O op de bissectrice van B ligt, raakt deze cirkel ook aan AB (in het punt S).
Dus:
BS = 3 en AS = 2.
De bissectrice snijdt de cirkel in de punten P en R en de lijn CS in Q (de hoek bij Q is recht).
Volgens de bissectrice-stelling is BC/BA = CO/AO = 3/5
Dus CO = 3/8 . 4 = 3/2 (= straal) en AO = 5/2.
Verdere berekeningen geven:

BO = 3/2Ö5 (via driehoek BCO), zodat
   BP = BO - PO = 3/2(Ö5 - 1)
   BR = BP + PR = 3/2(Ö5 - 1) + 3 = 3/2(Ö5 + 1)
Hieruit volgt dan
   BR / PR = (Ö5 + 1)/2 = f
Waaruit volgt, dat P = vmur(BR). ¨

figuur 5b 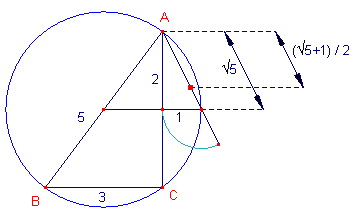sectio5b In nevenstaande figuur staat een andere constructie voor f in een 3-4-5-driehoek.
De wijze van construeren spreekt voor zichzelf.

4.2. De macht van een punt terug

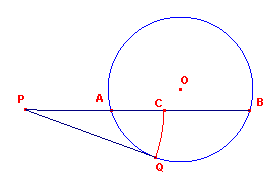figuur 6 sectio6 In figuur 6 is AB = PQ, waarbij PQ het raaklijnstuk is uit P aan de cirkel met middelpunt O.
Nu geldt voor de macht van het punt P tov. cirkel O:
PA x PB = PQ2, zodat
PA : PQ = PQ : PB, of
PA : AB = AB : (PA + AB)
We zien dus, dat A = vumr(PB).

Verder geldt voor het punt C, dat PC = PQ.
Nu is:
   PA = PC - AC = AB - AC
en ook
   BC = AB - AC, zodat
   PA = BC

We hebben nu:
   AB : BC = AB : PA = f
Dus ook C = vumr(AB).

4.3. Goniometrie terug

We lossen de vergelijking sin 2x = cos 3x op.
Hieruit volgt direct:
   sin 2x = sin(p/2 - 3x)
zodat we (oa.) vinden x = p/10.
De vergelijking laat zich als volgt herleiden:
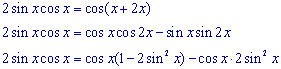
sectio5a_f
We laten de "trivale" oplossingen uit cos x = 0 voor wat ze zijn, zodat nu:
sectio5b_f
Hieruit vinden we dan als (positieve) oplossing:
sectio5c_f
zodat
   sin 18° = 1/(2f)
Wegens cos 36° = 1 - 2sin2 18° = 1 - 1/(2.Phi2), vinden we (na enige herleiding)
   cos 36° = f / 2

N.b.
Voor een afleiding van de goniometrische verhoudingen van de hoeken van 36º en 72º zie het artikel "Over de hoeken van 36º en 72º", januari 2006.
Klik hier om het artikel te downloaden (PDF-bestand; ca. 112 kB).

4.4. Phi als kettingbreuk terug
Op de pagina "Kettingbreuken" wordt een inleiding gegeven tot de theorie van de kettingbreuken.
Uit f 2 = f + 1 volgt:
   f = 1 + 1 / f
en dus ook
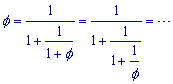
   sectio62_f
We vinden dus de oneindige kettingbreuk (zie de pagina "Kettingbreuken" voor de schrijfwijze):
   f = ]1, 1, 1, 1, 1, ...[
De benaderende breuken Pk/Qk van f kunnen we nu via een algoritme berekenen:
   ketting11
Hierin zijn de getallen ak de opvolgende waarden in ]a1, a2, ...[. Dus voor alle k hebben we in dit geval ak = 1.

k = 0 1 2 3 4 5 6 7 8 9    ...
Pk / Qk =  1/0 1/1 2/1 3/2 5/3 8/5 13/8 21/13 34/21 55/34 ...

Zie voor de tellers en noemers van de benaderende breuken paragraaf  6. Getallen van Fibonacci.

Zie ook de pagina "Logaritmische spiraal".

newy4.5 Een ring en een ellips - gulden ellips terug

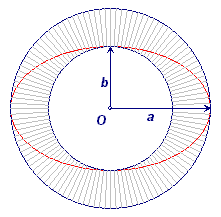sectio10 We gaan uit van twee in O concentrische cirkels met stralen a en b (a > b).
De oppervlakte van de ring is gelijk aan
   pa2 - pb2 = p(a2 - b2) ......(1)
De ellips met grote as gelijk aan 2a en kleine as gelijk aan 2b, en met O als middelpunt, heeft als oppervlakte
   pab ......(2)
Wanneer beide oppervlaktes gelijk zijn, vinden we uit (1) en (2):
   a2 - b2 = ab
   a2- ab - b2 = 0
waaruit we vinden dat a / b  = f
Opmerking - We zouden zo'n ellips dan (bij gelijke oppervlaktes dus) een gulden ellips kunnen noemen.

5. Gulden rechthoek en gulden driehoek terug

5.1. Gulden rechthoek terug

figuur 7a 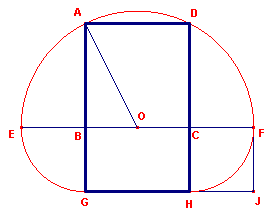sectio7 Uitgaande van een vierkant ABCD met zijde 1 construeren we de punten E en F via de cirkel O (het midden van BC) met straal OA (= ½Ö5).
Nu is EB = BG = CF = CH = ½Ö5 - ½ = (Ö5 - 1)/2 = 1/f.
Daardoor:
AG = AB + BG  = 1 + 1/f = (f  + 1)/f = f.
De zijden van rechthoek AGHD zijn dus 1 en f.
We noemen een dergelijke rechthoek waarvan de zijden zich verhouden als 1 : f een gulden rechthoek.

Opmerkingen
[1]
V(BGJF) = (1 + 1/f)(1/f) = 1/f  + 1/f 2 = (f + 1)/f 2 = 1
[2]
Bovenstaande constructie van een gulden rechthoek is niet de meest eenvoudige. Hieronder staat de meest gebruikte

figuur 7b 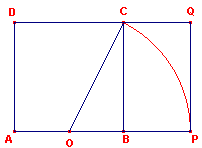sectio7b Uitgaande van vierkant ABCD met AB = 1 (O is het midden van AB) hebben we:
OC = ½Ö5.
Met OP = CO hebben we dan AP = ½ + ½Ö5.

N.b.
Op deze constructie kunnen we natuurlijk ook een constructie van de regelmatige vijfhoek baseren.
Zie daarvoor de pagina "Een andere constructie van de gulden snede" (deze website).
Zie verder ook Referentie [1].

[3]
Zie ook de pagina "Logaritmische spiraal", waarop in de gulden rechthoek via verdeling daarvan in een kleinere rechthoeken een spiraal kan worden getekend.
[einde Opmerkingen]

5.2. Gulden driehoek terug

figuur 8 sectio8 Een driehoek met hoeken van 36°, 72° en 72° heet gulden driehoek.
De bissectrice van hoek B snijdt de zijde AC in het punt D. Dan geldt
AD = BD = BC.
Nu is:
ABC ~ BCD (hh), zodat
AC : BD = BC : CD
of
AC : AD = AD : CD
Zodat D = vumr(AC).
Of ook:
AC = f  . AD.
Kiezen we BD = 1, dan is dus AC = AB = f.

Gevolg
We bekijken de oppervlaktes (V) van de verschillende driehoeken in figuur 8.
V(ABC) = ½AB . AC . sinA = ½f 2sin 36º
V(ABD) = ½BA . BD . sinABD = ½ . f . 1 . sin 36º = ½f sin 36º
V(BCD) = ½BC . BD . sinCBD = ½ . 1 . 1 . sin 36º = ½ sin 36º
Zodat:
V(ABC) : V(ABD) : V(BCD) = f 2 : f : 1.
[einde Gevolg]

Opmerking
Zie ook de pagina "Logaritmische spiraal", waarop in de gulden driehoek via verdeling daarvan in een kleinere driehoeken een spiraal kan worden getekend.
[einde Opmerking]

6. Getallen van Fibonacci terug
De (meetkundige) rij getallen
   1, f, f 2, ...
heeft ook de additieve eigenschap un + 1 = un + un - 1 (met n = 2, 3, ...).
Dit volgt uit het feit, dat f 2 = f + 1.
Zo is f 3 = f . f 2 = f(f + 1) = f 2 + f = 2f + 1
De rij kan dus ook geschreven worden als
   1, f, 1 + f, 1 + 2f, 2 + 3f, ...

Definitie
Rijen met de eigenschap un + 1 = un + un - 1 worden ook wel Lucas-rijen genoemd
(naar Edouard Lucas - Francois Edouard Anatole Lucas, 1842-1891, Frankrijk).

Geven we u1 en u2, dan ligt de rij vast.
Twee voorbeelden:
[1]
u1 = 2, u2 = 1
Lucas-rij: 2, 1, 3, 4, 7, 11, ...
De getallen in deze rij heten Getallen van Lucas (Lucas-numbers; zie ook Referenties).
[2]
u1 = 5, u2 = 2
Lucas-rij: 5, 2, 7, 9, 16, 25, 41, 66, 107, 173, 280, 453, 733, ..., 13153, 21282, ...
We berekenen van deze rij voor enkele waarden van n de uitdrukking un+1/un:
   16 / 9 = 1,7777...
   453 / 280 = 1,6178...
   733 / 453 = 1,6181...
   21282 / 13153 = 1,61803...
We zien, dat de waarden van un+1/un de waarde van f  = (Ö5 + 1)/2 benaderen.
[einde Voorbeelden]

De rij van Fibonacci
We kiezen nu, als in de voorbeelden:
u1 = 1, u2 = 1
De eerste 40 termen van de bijbehorende Lucas-rij staan in de volgende tabel.

n  un   n un   n un   n un
     1 1       11 89       21 10946       31 1346269
2 1   12 144   22 17711   32 2178309
3 2   13 233   23 28657   33 3524578
4 3   14 377   24 46368   34 5702887
5 5   15 610   25 75025   35 9227465
6 8   16 987   26 121393   36 14930352
7 13   17 1597   27 196418   37 24157817
8 21   18 2584   28 317811   38 39088169
9 34   19 4181   29 514229   39 63245986
10 55   20 6765   30 832040   40 102334155

Deze elementen van deze rij heten getallen van Fibonacci (zo genoemd door Lucas in 1877).
Leonardo van Pisa (genaamd Fibonacci, Filius Bonaccii, wat "zoon van Bonaccio" betekent) leefde ca. 1175-1250.
Fibonacci publceerde in zijn boek Liber Abaci het befaamde "konijnenvraagtuk" waarvan de getallen van Fibonacci de oplossing zijn.
Ook voor de getallen van Fibonacci geldt, dat un+1/un de waarde van f  = (Ö5 + 1)/2 benaderen:
   u15/u14 = 1,618037
   u25/u24 = 1,618033
We kunnen bewijzen dat
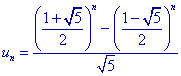
   sectio6_f
Klik hier voor een bewijs van de formule.
De formule werd het eerst gepubliceerd in 1730 door Abraham de Moivre (1667-1754, geboren in Vitry, Frankrijk).
De formule wordt echter vaak aangeduid als de formule van Binet (naar Jacques Philippe Marie Binet, 1786-1856, geboren in Rennes, Frankrijk). Binet bewees de formule in 1843.

We kunnen inderdaad ook bewijzen, dat

Stelling
Voor elementen un van elke Lucas-rij geldt (voor "grote" waarden van n): un+1 / un »     f

Klik hier voor een bewijs van deze stelling voor de rij van Fibonacci.

Opmerking
Een eenvoudig bewijs van de stelling voor de rij van Fibonacci kan ook worden geleverd door f  te ontwikkelen in een kettingbreuk.
Zie voor een aanzet daartoe paragraaf 4.4. Phi als kettingbreuk.
[einde Opmerking]

7. Referenties terug

Zie ook de pagina "Logaritmische spiraal".

[1] HANS BÄR: Tekengalerij (http://members.chello.nl/~jlmbar/)
[2]     H.E. HUNTLEY: The Divine Proportion. Dover Publications Inc., New York (1970)
[3] ROBERT LAWLOR: Sacred Geometry. Thames & Hudson Ltd., Londen (1982)
[4] N.N. WOROBJOW: Die Fibonaccische Zahlen. VEB Verlag, Berlijn (1971; vertaling uit het Russisch)

- Referenties op Internet kunnen worden gevonden met de sleutelwoorden "golden section ratio fibonacci";
oa. over Lucas-numbers en Fibonacci-numbers (door R. Knott - Surrey University, Guildford, UK).

begin pagina

[sectioaurea.htm] laatste wijziging op: 16-02-10