De formule van Binet en een stelling van Lucas

Binet | Lucas  ][  Gulden snede | Elementen | Meetkunde | Getallentheorie

---

Zie ook de pagina "Gulden snede en getallen van Fibonacci".

1. De formule van Binet

Stelling Voor de getallen un met un+1 = un + un-1 (met n > 1, u1 = 1 en u2 =1) geldt 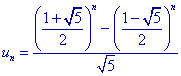    (formule van Binet; naar Jacques Philippe Marie Binet, 1786-1856, geboren in Rennes, Frankrijk, gepubliceerd in 1843)

Bewijs:
De getallen u_n vormen de rij van Fibonacci: 1, 1, 2, 3, 5, 8, ...
We schrijven op deze pagina p in plaats van f.
De getallen p = (1 + Ö5)/2 en p' = (1 - Ö5)/2 zijn de wortels van de vergelijking x² - x - 1 = 0 (zie de pagina "Gulden snede").
Voor de formule van Binet kunnen we dus schrijven:
   
Op grond van p² - p - 1 = 0 waaruit volgt dat p² = p + 1 hebben we
   p³ = p² + p = p + 1 + p =           2p + 1
   p⁴ = 2p² + p = 2(p + 1) + p =     3p + 2
   p⁵ = 3p² + 2p = 3(p + 1) + 2p = 5p + 3
   p⁶ = 5p² + 3p = 5(p + 1) + 3p = 8p + 5
   ...
De coëfficiënten en constanten in de rechter leden van de uitdrukkingen hierboven zijn opvolgende Fibonacci-getallen (hetgeen eenvoudig met volledige inductie kan worden aangetoond).
We kunnen dus schrijven:
   pⁿ = F(n) ^. p + F(n-1)
Uiteraard geldt ook
   p' ⁿ = F(n) ^. p' + F(n-1)
Nu is
   pⁿ - p' ⁿ = F(n) ^. p - F(n) ^. p' = F(n) ^. (p - p')
zodat
   F(n) = (pⁿ - p' ⁿ) / (p - p')
Echter p - p' = Ö5, zodat we inderdaad vinden, dat
      
¨

2. Een stelling van Lucas

Stelling (van Lucas) Voor elementen un van de rij van Fibonacci geldt (voor "grote" waarden van n): un+1/un » f

Bewijs:
Daarbij gebruiken we de formule van Binet en het feit, dat p / p' = - p².
We schrijven F(n) = u_n, waarbij F(1) = 1 en F(2) = 1.
Nu is volgens de formule van Binet:
   
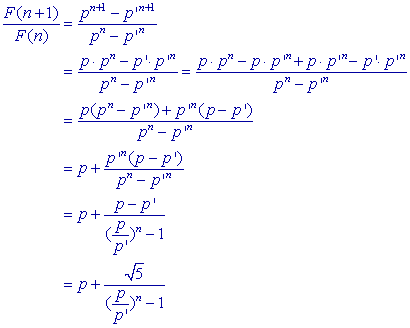
Nu is
   
Deze uitdrukking neemt voor grote waarde van n onbegrensd toe, immers p > 1.
Het tweede lid in de uitdrukking voor F(n+1)/F(n) nadert daardoor tot 0.
Zodat
   
¨

---

[sectioaurea2.htm] laatste wijziging op: 15-sep-01