De logaritmische spiraal

Overzicht ][ Gulden snede | Meetkunde

---

Zie ook de pagina "Cabri-FAQ 28 - Hoe teken je een spiraal?"

Overzicht

1. Poolcoördinaten
2. Roteren en vermenigvuldigen
3. Logaritmische spiraal
4. Eigenschappen
5. Loxodromen
6. De logaritmische spiraal en de gulden rechthoek
7. Draaivermenigvuldiging
8. Vermenigvuldigings- en rotatiecongruent
9. De logaritmische spiraal en de gulden driehoek
10. Referenties

---

1. Poolcoördinaten

figuur 1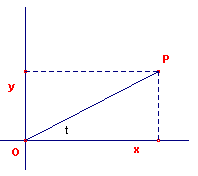

De plaats van een punt P in een vlak kan niet alleen worden vastgelegd door een tweetal coördinaten (x, y) tov. een orthonormaal assenstel, maar ook door de afstand r van P tot het punt O en de hoek t die OP maakt met de positieve x-as.

Deze coördinaten heten de poolcoördinaten van P: (r, t). Het verband tussen beide soorten coördinaten is als volgt:

2. Roteren en vermenigvuldigingen

We beschouwen nu de volgende afbeeldingen van het vlak op zichzelf:
R: (r, q ) ® (r, q  + v) waarbij v continu verandert over de verzameling R van de reële getallen
Het beeld van het punt (a,0) is dan de cirkel r = a.
R heet continue rotatie.

V:

(x,y) ® (vx, vy) waarbij v continu verandert over de verzameling R van de reële getallen
Het beeld van (a,0) is dan de positieve x-as, als v > 0).
V heet continue vermenigvuldiging.

3. Logaritmische spiraal

De afbeelding D = VR heet continue draaivermenigvuldiging.
We laten nu de vermenigvuldigingsfactor v afhangen van de grootte van de rotatiehoek t:
m is de factor bij de draaiing over een hoek van 1 rad;
dus:
m² is de factor bij draaiing over een hoek van 2 rad;
algemeen:
m^v is de factor bij draaiing over een hoek van v rad.

Door D = VR wordt het algemene punt (r, q ) afgebeeld op het punt (m^vr, q  + v).
Voor het beeldpunt van (a,0) hebben we dan:

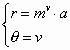
Eliminatie van v hieruit geeft:
Deze poolvergelijking is de vergelijking van een kromme lijn.
De verzameling beeldpunten van het punt (a,0) heet logaritmische spiraal, ook wel equiangulaire spiraal (zie figuur 2).

figuur 2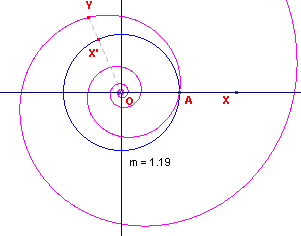

In figuur 2 is OA = a en m = 1,19. Het punt X ligt op de x-as. Het punt X’ ligt op de cirkel (O,OA) zodat bg(OX’) = t = OX (gericht). Het punt Y ligt zo, dat OY = mq . OX’. De meetkundige plaats van het punt Y is dan de logaritmische spiraal (bij m). Het punt O heet de pool van de spiraal. Het lijnstuk OA heet de hoofdstraal.

4. Eigenschappen

[1]

figuur 3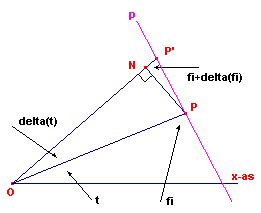

Zij P (r, q ) een punt van de spiraal. De hoek tussen de raaklijn in P aan de spiraal en de voerstraal OP zij f . Nu is dr/dq = a . mq . ln(m) = r . ln(m) ……(1) Zijn P en P’ twee punten van de spiraal, waarbij P’ zo gelegen is, dat de raaklijn p in P de limietstand is van de lijn PP’ als P’ naar P nadert (zie figuur 3). In deze figuur is PN loodrecht op OP’.

Dan geldt:
sin(D q ) = PN/r, zodat PN = r.sin(D q ).
Voor kleine D q is sin(D q ) = D q , zodat ook PN = r. D q .
Nu vinden we eenvoudig:
……(2)
Uit (1) en (2) vinden we dan tan f = 1 / ln(m).
De hoek f (de hoek tussen brandpuntvoerstraal en raaklijn) is dus constant. Vandaar dat ook de naam equiangulaire spiraal (in figuur 2 is de hoek f ongeveer 80°).

Een andere schrijfwijze voor de poolvergelijking luidt op basis hiervan: r = ae^{q . cot ( f )}.

[2]

Stelling De logaritmische spiraal wordt door een vermenigvuldiging tov. zijn pool met de factor m2p afgebeeld op zichzelf.

Bewijs:

r. m^2p = a m^t . m^2p = a . m^t+2p .¨

Zie ook de paragraaf Loxodromen.

[3]

Stelling De logaritmische spiraal gaat door inversie tov. de cirkel (O, a) over in een logaritmische spiraal die het spiegelbeeld is van de oorspronkelijke spiraal in de hoofdstraal.

Bewijs:

figuur 4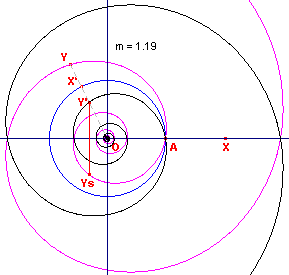

Zij Y’ het beeld van Y bij de bedoelde inversie. Dan geldt (per definitie): OY . OY’ = a2. Dus: OY’ = a2 / OY = a2 / r = a2 / (amq ) = am-q . Het punt Y’ is dus het spiegelbeeld van een punt Ys van de oorspronkelijke spiraal in OA (de x-as). ¨

[4]

We passen de vermenigvuldiging V(O,m) toe op de spiraal. We krijgen dan een nieuwe spiraal V(S).
Hiervoor geldt:
r = m . am^t = am^t+1.
Maar hieruit volgt dus, dat voor de spiraal V(S) ook geldt dat deze kan ontstaan door een rotatie R(O,1).
Dus: V(S) = R(S).
Door de afbeelding V^invR gaat de spiraal dus over in zichzelf.

Gevolg

Als een spiraal wordt rondgedraaid, lijkt hij groter of kleiner te worden.

5. Loxodromen

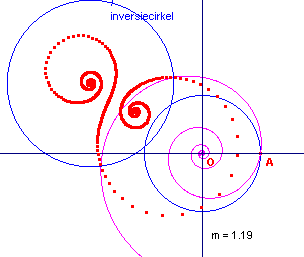
In onderstaande figuur zijn de inversen van de spiraal tov. van een cirkel getekend.
Deze kromme lijnen heten loxodromen.

figuur 5a	figuur 5b
willekeurige inversiecirkel	middelpunt van de inversiecirkel op de spiraal

figuur 5c
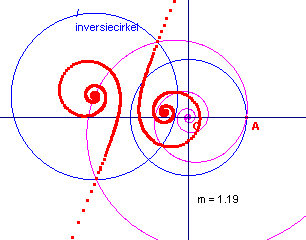
	In figuur 5c is het middelpunt van de inversiecirkel het puntspiegelbeeld van A in O. Verder gaat de inversiecirkel door het punt O. Opmerking De loxodromen zijn in Cabri Geometry II bepaald via de optie Voorkeuren | Meetkundige plaats | Punten verbinden | U i t. [einde Opmerking]

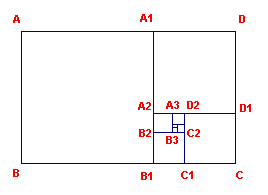
6. De logaritmische spiraal en de gulden rechthoek

We gaan uit van de gulden rechthoek ABCD. Hierin is dus AD = p . AB, waarbij p = (1 + Ö5)/2 (zie hiervoor de pagina "Gulden snede").
We merken nog op, dat voor p geldt: p² – p – 1 = 0.

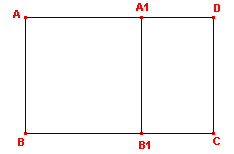We kiezen op AD het punt A1 en op BC het punt B1, met AA1 = AB = A1B1. Van de rechthoek is dus een vierkant afgesneden. Nu is A1D = AD – AB = p.AB – AB = (p – 1)AB. Vermenigvuldiging van beide leden met p geeft nu: p . A1D = (p2 – p)AB. Wegens de "gulden snede" is nu p2 – p = 1, zodat ook CD = AB = p . A1D. A1B1CD is dus eveneens een gulden rechthoek.

Van deze gulden rechthoek kunnen we weer een vierkant afsnijden, waardoor er weer een gulden rechthoek overblijft.
We krijgen daardoor dus een rij gulden rechthoeken:
ABCD, A₁B₁CD, A₂B1CD₁, A₂B₁C₁D₂, … (zie figuur 6b).

figuur 6b	figuur 6c

Uit de constructie van de rij rechthoeken volgt, dat er een vermenigvuldiging V = (C, k) bestaat zodat V(ABCD) = A₂B₁CD₁.
Uitgaande van AB = 1, is de vermenigvuldigingsfactor k gelijk aan AD/A₂D₁ = p/A₁D = p / (p – 1) = p², immers
p² – p = p(p – 1) = 1.

Gevolg

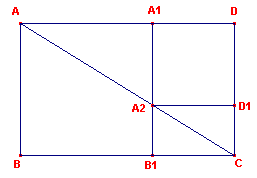
De punten A, A₂ en C zijn collineair.

Hulpstelling In de gulden rechthoek ABCD, waarin ABEF een vierkant is, geldt AC_|_DE.

Bewijs:

figuur 6d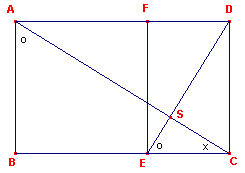

Uit de gelijkvormigheid van de rechthoeken ABCD en ECDF volgt dat daarin BAC = CED. De driehoeken ABC en ECS hebben daardoor twee gelijke hoeken, zodat ABC~ESC. Hoek S is dus recht. ¨

7. Draaivermenigvuldiging

We bekijken nu in de gulden rechthoek ABCD de tweede rechthoek A₁B₁CD. Nu geldt volgens de hulpstelling dat AC _|_ B₁D (zie figuur 7).

figuur 7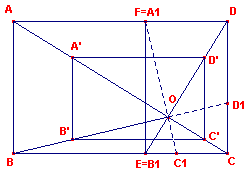

Zij nu O het snijpunt van AC en B1D. Passen we nu op ABCD een vermenigvuldiging V toe met centrum O en factor f = 1/p dan is V(ABCD)=A’B’C’D’. Nu is: A’D’ = CD en A’B’ = A1D. Bij de rotatie R=(O, -90°) hebben we dus: R(A’B’C’D’)=DA1B1C.

Zij nu F de samengestelde afbeelding van R en V, dus F = RV, dan is:
F(A) = D; F(B) = A₁; F(C) = B₁; F(D) = C.Verder hebben we:
OD = 1/p . OA, of OA = p . OD en ook A₁A = p.A₁D, zodat
OA : A₁A = OD : A₁D
of
OA : OD = A₁A : A₁D
Volgens de omgekeerde bissectricestelling is dan OA₁ is de bissectrice van hoek AOD.
Zodat:
De lijnen A₁C₁ en BD₁ gaan door O en delen de hoeken tussen B₁D en AC middendoor.
De afbeelding F toegepast op de rij van gulden rechthoeken geeft dan de volgende rijen van toegevoegde punten:
   I  : B ®  A₁ ®  D₁ ®  C₁ ®  B₂ ®  …
   I I : A ®  D ®  C ®  B₁ ®  A₂ ®  …
De afbeelding F is een draaivermenigvuldiging met centrum O, factor 1/p en hoek -90° .
De inverse afbeelding van F is dus ook een draaivermenigvuldiging met centrum O, factor p en hoek +90° .
Overgang op poolcoördinaten (met pool O) geeft nu:
   F    : P(r, q ) ® P’(p / r, q - p /2)
   F^inv: P(r, q ) ® P’(p . r, q + p /2)
waarbij we OD₁ als x-as kiezen en OD₁ = 1.
De poolcoördinaten van de punten uit serie I hierboven zijn dan:
B(p², p ); A₁(p, ½ p ); D₁(1,0); C₁(1/p, - ½ p ); B₂(1/p², - p ); …
Voor deze puntenrij hebben we dan de algemene formule:
   r = pⁿ met q = ½ p n (n geheel)
De poolcoördinaten van de punten uit rij I voldoen dus aan: r = p^{2 q  / p}

We hebben nu dus bewezen:

figuur 8a		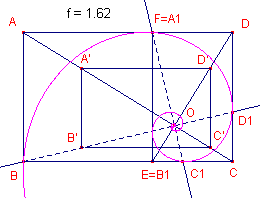Stelling De punten B, A1, D1, C1, … (serie I) liggen op de logaritmische spiraal met poolvergelijking: r = p2 q  / p .
figuur 8b		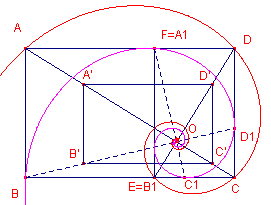Gevolg Ook de punten A, D, C, B1, … liggen op een logaritmische spiraal (zie ook de volgende paragraaf). Kiezen we weer O als pool en nu OB1 als hoofdstraal (met OB1 = 1), dan hebben we:    A(p3, 3p /2); D(p2, p ); C(p, p /2); B1(1, 0), … De poolvergelijking van deze spiraal is dan ook nu (maar nu tov. de hoofdstraal OB1):    r = p2 q  / p . Beide spiralen zijn dus congruent.

8. Vermenigvuldigings- en rotatiecongruentie

We kiezen de dragers van de lijnstukken OD₁ (OD₁ = 1) en OA₁ als assen van een coördinatenstelsel.

figuur 9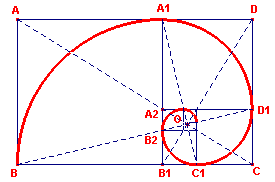

Op basis van de in de vorige paragraaf gevonden poolcoördinaten vinden we nu als rechthoekige coördinaten:    B2(-p-2, 0), C1(0, -p-1), A1(0, p), B(-p2, 0). De lijnen B2A1 en C1B hebben dan opvolgend de vergelijkingen: 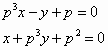    Op basis van de eigenschappen van p hebben we dan voor het snijpunt van beide lijnen:

B₁(- ½, - ½ ) of in poolcoördinaten B₁(Ö ½, -3p /4).
De punten A₂, B₁, C, D en A liggen dus op de spiraal r = 2^{- ½} pⁿ met opvolgend de argumenten -5p /4 (n = -1), -3p /4 (n=0), -p /4 (n=1), p /4 (n=2), 3p /4 (n=3).
In dit geval geldt dat q = ¼ (2n – 3) p , waaruit volgt dat n = 2q /p +1½.
De tweede spiraal kan zodoende geschreven worden als r = 2^{- ½} p^{2q /p +1½}.

Gevolg
Deze spiraal kan uit de eerste spiraal worden verkregen door een vermenigvuldiging tov. O met de factor a = 2^{- ½} p^1½.
Maar ook: de tweede spiraal kan uit de eerst spiraal worden door een rotatie over de hoek ^plog(a).
Met andere woorden:
Beide spiralen zijn vermenigvuldigings- en rotatiecongruent.

9. De logaritmische spiraal en de gouden driehoek

Op dezelfde manier waarop hierboven de logaritmische spiraal is geconstrueerd in de gulden rechthoek, kan een logaritmische spiraal toegevoegd worden aan een gulden driehoek.

figuur 10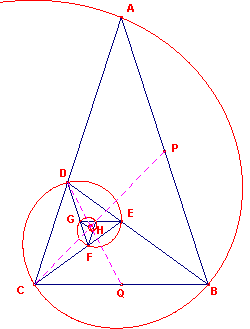

De driehoeken ABC, BCD, CDE, DEF, EFG, FGH, ... zijn gelijkvormig op basis van de constructie van de bissectrice van de hoeken B, C, D, E, F, G, … De pool O van de spiraal is het snijpunt O van de zwaartelijnen CP (van driehoek ABC) en DQ (van driehoek BCD). De hoek tussen deze lijnen is nu 72°.

10. Referenties

[1]		H.S.M. COXETER, Introduction to Geometry, Wiley & Sons, New York (1961)
[2]		H.E. HUNTLEY, The Divine Proportion, Dover Publications Inc., New York (1970)
[3]		ROBERT LAWLOR, Sacred Geometry, Thames & Hudson Ltd., Londen (1982)
[4]		N.N. WOROBJOW, Die Fibonaccische Zahlen, VEB Verlag, Berlijn (1971; vertaling uit het Russisch)

Zie ook de pagina "Gulden snede".

---

[logspiraal.htm] laatste wijziging op: 12-jul-05