Cabri-FAQ (28)

Vorige

Begin

Volgende

Vraag 28
Hoe teken je een spiraal?

Antwoord
We gaan uit van een vaste halve lijn met beginpunt O.
Een spiraal is een kromme lijn waarvan voor elke punt P van die lijn geldt, dat OP een (stijgende) functie is van de hoek die OP maakt met die gegeven halve lijn.
OP wordt hierbij meestal aangegeven met de letter r (de voerstraal). De hoek wordt aangegeven met de Griekse letter f (fi) of q (thêta). De hoek wordt hierbij gemeten in radialen.
Een eenvoudig voorbeeld is dus: r = f (in dit geval mag f dus niet negatief zijn).
We construeren deze spiraal.

Opmerking - Een getal tussen ( en ) in de Cabri-functies verwijzen naar een eerder geconstrueerd object (nl. het object in de door dat nummer aangegeven constructiestap. Dat object moet dan geselecteerd worden.

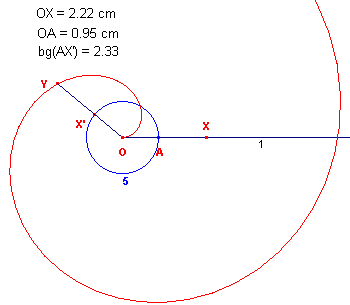We kiezen een punt O en een punt A.
We kiezen OA als eenheid, dus OA = 1.
De constructiestappen daarna zijn:
1 - HalveLijn(OA)
2 - PuntOpObject(1) = X
Het punt X zal gaan dienen als het "aandrijvende" punt van de spiraal.
3 - Lengte(O,X) = OX
4 - Lengte(O,A) = OA
5 - Cirkel(O, A)
We moeten nu de waarde van OX overbrengen op de cirkel.
6 - MaatOverbrengen(waarde OX, 5, A) = X'
Via Cabri's Rekenmachine berekenen we nu OX/OA (OX = a, OA = b).
7 - Rekenmachine(a, /, b, =); dit geeft bg(AX') = f.
Hierdoor is bg(AX') uitgedrukt in radialen.

Nu moet het lijnstuk OY = r, waarbij dus Y het punt op de spiraal is (het "aangedreven" punt), de lengte krijgen van bg(AX').
Dit doen we met een vermenigvuldiging van het punt X' met de waarde van bg(AX') = f ten opzichte van het punt O.
8 - Vermenigvuldiging(X', O, f) = Y
9 - MeetkundigePlaats(Y, X)
En we vinden de spiraal.

Klik hier voor een CabriJavapplet bij het bovenstaande.

Opmerking
Een spiraal als hierboven getekend, heet ook wel Archimedische spiraal.
Zie ook de pagina "Logaritmische spiraal".
[einde Opmerking]

Zie Download

Vorige

Begin

Volgende

[faq28.htm] laatste wijziging op: 24-03-04