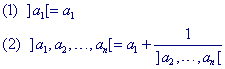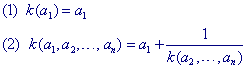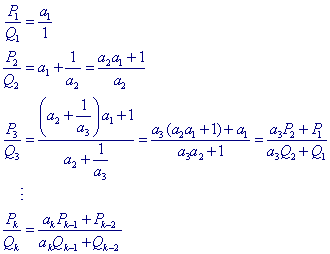Kettingbreuken
- Gevolg van de Euclidische algoritme
- Definitie kettingbreuk
- Benaderende breuken
- Algoritme
- Geheeltallige oplossingen van ax + by = c
1. Gevolg van de Euclidische algoritme
![]()
Zij A = t / m een breuk met ggd(t,m) = 1.
De getallen t en m heten in dit geval onderling ondeelbaar of ook wel relatief
priem.
Volgens de Euclidische algoritme (zie ook de pagina "Deelbaarheid")
kunnen we nu getallen ai en ri vinden met
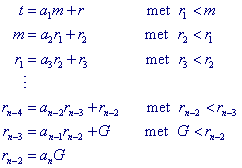
In de laatste twee regels is G = ggd(t,m) (een en andere geheel op basis van de Euclidische algoritme).
Voor G = 1 hebben we dus rn - 2 = an.
Op basis hiervan vinden we
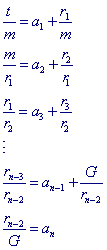
2. Definitie kettingbreuk
![]()
Uit hetgeen gevonden is in paragraaf 1 kunnen we nu eenvoudig (per regel)
afleiden:
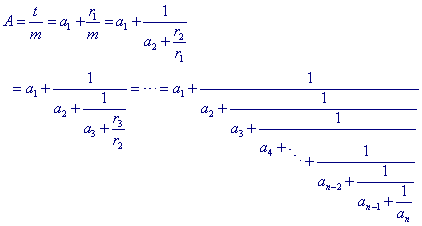
| Definitie De hierboven staande schrijfwijze voor het rationale getal A heet kettingbreuk (A is ontwikkeld in een kettingbreuk). Schrijfwijze: A =]a1, a2, a3, ..., an[ of ook wel A = k(a1, a2, a3, ..., an). De getallen ai heten de elementen van de kettingbreuk. |
Recursieve definitie
|
Toelichting bij de recursieve definitie
Regel (1) in de definitie zegt wat een kettingbreuk is bestaande uit één element.
Regel (2) in de definitie zegt wat een kettingbreuk is bestaanden uit n
elementen, als de kettingbreuk met n-1 elementen bekend is.
[einde Toelichting]
Voorbeeld
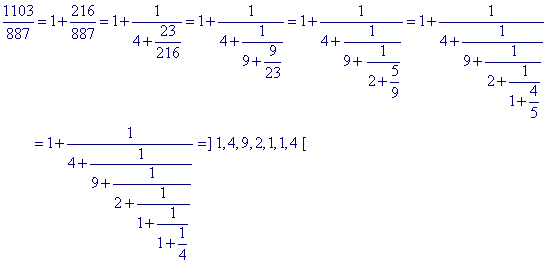
[einde Voorbeeld]
Afwijkende vormen van kettingbreuken zijn bijvoorbeeld
(1) ]a1, a2, ..., an-2, ]an-1, an[[
(2) ]a1, a2, ..., an-3, ]an-2, an-1, an[[
(3) ]a1, a2, ..., an-1, ]an - 1, 1[[.
In dit laatste geval (3) is
]an - 1, 1[ = (an - 1) + 1/1
= an
zodat dus
]a1, a2, ..., an-1, ]an - 1, 1[[ = ]a1, a2, ..., an[
3. Benaderende breuken
![]()
Voor A = ]a1, a2, ..., an[ schrijven we
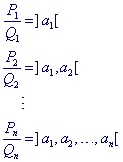
zodat
![]()
| Definitie De uitdrukking Pi / Qi = ]a1, a2, ..., ak[ met k = 1, 2, ..., n, noemen we een benaderende breuk van A=]a1,a2, ..., an[. |
4. Algoritme ![]()
Op basis van de uitdrukking voor Pk / Qk (in het Gevolg in paragraaf 3):
![]()
kunnen we een algoritme voor de berekening van de waarde van een kettingbreuk ontwerpen.
We merken op, dat uit de laatste formule voor k = 2 een waarde kan worden gevonden voor P0
en Q0 (de 0-de benaderende breuk van elke kettingbreuk).
We vinden:
P2 = a2P1 + P0 of a2a1
+ 1 = a2a1 + P0
Q2 = a2Q1 + Q0 of a2
= a2 . 1 + Q0
Hieruit volgt dus: P0 = 1 en Q0 = 0.
Voorbeeld
Uitgaande van A = ]3,7,2,5,11[ vinden we de opeenvolgende benaderende breuken uit
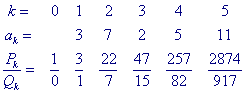
Dus A = 2874/917.
[einde Voorbeeld]
Uit de genoemde uitdrukking voor Pk / Qk
kunnen we eveneens afleiden:
![]()
zodat we voor de teller hiervan vinden:
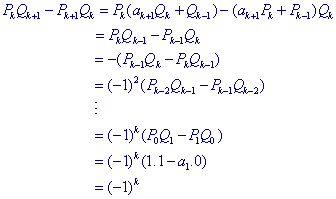
en dus
![]()
Deze relatie geeft een eenvoudige uitdrukking voor A = Pn / Qn:
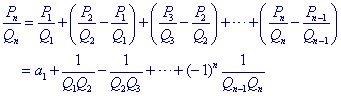
Opmerking
Zie voor een voorbeeld van een oneindige kettingbreuk de pagina "Gulden snede en Getallen van Fibonacci".
[einde Opmerking]
5. Geheeltallige oplossingen van ax
+ by = c ![]()
Uitgangspunt is een vergelijking
ax + by = c
met a, b, c geheel en waarbij ggd(c, ggd(a,b)) = 1.
Als G = ggd(a,b) | c, dan herleiden we via deling door G.
Zonder de algemeenheid geweld aan te doen kunnen we stellen, dat ggd(a,b)=1.
Particuliere oplossing
Zij x = x1, y = y1 een oplossing van de vergelijking.
Bekijk nu voor iedere gehele t : x = x1 + bt , y = y1
- at.
Nu is bij substitutie:
ax + by = ax1 + abt + by1 - abt = ax1 +
by1 = c
Dus ook x = x1 + bt, y = y1 - at is een oplossing van de
vergelijking (vooor iedere t)
Stel x2, y2 is een tweede oplossing van de vergelijking.
Nu hebben we
ax1 + by1 = c
ax2 + by2 = c
Zodat
a(x2 - x1) = b(y1 - y2)
Dus b | a(x2 - x1)
Er is dus een t met bt = x2 - x1, zodat at = y1 - y2.
Elke tweede oplossing van de vergelijking wordt dus gevonden uit x = x1 + bt, y
= y1 - at.
We hebben nu dus bewezen
| Stelling 1 Als x1, y1 een oplossing is van ax + by = c, dan is de algemene oplossing van de vergelijking x = x1 + bt, y = y1 - at. De oplossing x1, y1 heet een particuliere oplossing van de vergelijking. |
Opmerking
Door invoering van een nieuwe veranderlijke, -x of -y, kan er steeds voor gezorgd worden,
dat a > 0 en b > 0.
[einde Opmerking]
Het vinden van een particuliere oplossing
Zij nu a / b = ]a1, a2, ..., an[ = Pn/ Qn, zodat dus
Pn = a en Qn = b.
We hebben a / b dus in een kettingbreuk ontwikkeld.
In paragraaf 4 hebben we afgeleid, dat PnQn+1 - Pn+1Qn
=(-1)n.
Stel nu x = (-1)nQn-1 en y = (-1)n - 1Pn-1
Nu is, bij substitutie,
| ax + by | = | Pn . (-1)nQn-1 + Qn . (-1)n - 1Pn-1 |
| = | (-1)n (PnQn-1 - QnPn-1) | |
| = | (-1)2n | |
| = | 1 |
| Stelling 2 x = (-1)nQn-1 , y = (-1)n - 1Pn-1 is oplossing van de vergelijking ax + by = 1, waarin Pn-1/Qn-1 de (n-1)-de benaderende breuk is van a/b. cx, cy is dan een particuliere oplossing van de vergelijking ax + by = c. |
[einde Gevolg]
Voorbeelden
[1]
We lossen op de vergelijking 8 x + 11 y = 417
Nu is
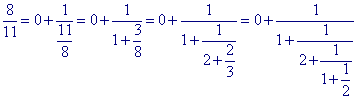
zodat 8 / 11 =] 0,1,2,1,2 [, met n = 5.
De 4-de benadering van 8/11 is dan dus
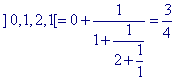
Dus Pn-1 = 3 en Qn-1 = 4
Met het bovenstaande Gevolg vinden we dus de algemene oplossing:
x = -4 . 417 + 11 t
y = 3 . 417 - 8 t
Voor de positieve oplossingen geldt 1668/11 < t
<1251/8. Dit is juist voor
| t = | 152 | 153 | 154 | 155 | 156 |
| x = | 4 | 15 | 26 | 37 | 48 |
| y = | 35 | 27 | 19 | 11 | 3 |
[2]
31 x - 51 y = 22
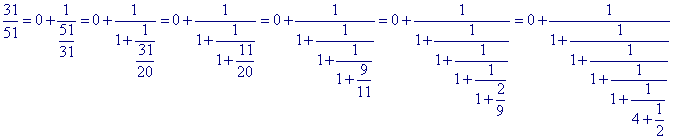
Dus 31/51 = ] 0,1,1,1,1,4,2 [ met n = 7.
] 0,1,1,1,1,4 [ = 14/23, zodat de algemene oplossing van 31 x - 51 y
= 22 gelijk is aan
x = -23 . 22 + 51 t = -506 + 51 t
-y = 14 . 22 + 31 t = -308 + 31 t
of ook
x = 5 + 51 u
y = 2 + 31 u
De positieve oplossingen vinden we voor u > 0.
[3]
2874 x + 917 y = 1.000.000
2874/917 = ] 3,7,2,5,11 [ met n = 5.
] 3,7,2,5 [ = 257/82.
Dus
x = -82 . 106 +917 t
y = 257 . 106 - 2874 t
Voor x > 0 hebben we t > 82 . 106 / 917 = 89422,028...
Voor y > 0 hebben we t < 257 . 106 / 2874 = 89422.40...
Er zijn dus geen positieve oplossingen van deze vergelijking.
Het bovenstaande kan snel worden geconcludeerd op basis van de hieronder
staande Stelling 3.
| Stelling 3 Voor natuurlijke getallen a, b, c is de vergelijking ax + by = c met ggd(a,b) = 1 is met natuurlijke getallen oplosbaar als c > ab. |
Bewijs:
Stel x=x1, y=y1 is een oplossing van ax +by = 1. Dat
wil zeggen
ax1 + by1 = 1
waaruit dus volgt dat y1 = (1 - ax1)/b.
De algemene oplossing van ax + by = c is dan
x = cx1 - bt
y = cy1 + at
Voor x > 0 hebben we dan t < cx1/b
Voor y > 0 hebben we t > -cy1/a = - (c - acx1)/ab = cx1/b
- c/ab
Of te wel
cx1/b - c/ab < t < cx1/b
Voor c/ab > 1 is er tenminste één gehele waarde van t tussen de beide grenzen.
Met andere woorden voor c > ab heeft de vergelijking positieve oplossingen.¨
[ketting.htm] laatste wijziging op: 13-09-2001