Eigenschap van de hoogtelijn

Stelling  |  Opmerking  ][ Kegelsneden

Stelling
In een rechthoekige driehoek waarin de hoogtelijn h de hypotenusa verdeelt in stukken p en q geldt h2 = pq.

1e bewijs:

figuur 1 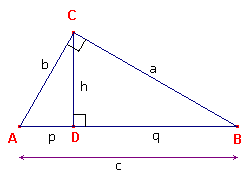imagesam_hoog Uitgaande van de stelling van Pythagoras hebben we (zie figuur 1):
   h2 = b2 - p2
en
   h2 = a2 - q2
Optelling van beide geeft dan
   2h2    = (a2 +b2) - (p2 + q2)
   = c2 - (p + q)2 + 2pq
   = c2 - c2 + 2pq

En dus h2 = pq. ¨

2e bewijs:
Uit de gelijkvormigheid van de driehoeken ADC en CDB (zie figuur 1) vinden we
   DC : AD = DB : CD
of
   h : p = q : h
Zodat opnieuw blijkt dat
   h2 = pq ¨

Opmerking
Zoals reeds vermeld (op de pagina Kegelsneden volgens Apollonius) is de stelling gebaseerd op propositie 14 uit Boek II van de Elementen van Euclides.
Deze propositie luidt
   Een vierkant te construeren, gelijk aan een gegeven rechtlijnige figuur.

In deze propositie geeft Euclides een constructie van een vierkant, waarvan de oppervlakte gelijk is aan de oppervlakte van een willekeurige vierhoek.
Bij deze constructie wordt die vierhoek eerst equivalent getransformeerd in een rechthoek
Impliciet wordt daarmee dan het bewijs van bovenstaande stelling geleverd.
De constructie is eigenlijk de gewone constructie van de middenevenredige van twee lijnstukken die in de hedendaagse (?) planimetrie wordt toepast.
[einde Opmerking]

terug naar Kegelsneden Kegelsneden terug naar Boek II Terug naar Boek II begin pagina Top

[am_hoog.htm] laatste wijziging op: 16-05-1999