Pooltransformatie

Overzicht ][ Pool en poollijn | Projectieve meetkunde | Meetkunde

Zie ook: Kegelsneden en hun vergelijkingen
Zie ook: Cabri-werkblad Poolafbeelding en reciproke afbeelding

0. Overzicht

Definities
Enveloppe, kegelsneden
     2.1. De enveloppe als beeld
     2.2. Het beeld van een cirkel
               2.2.1. Een cirkel concentrisch met de inversiecirkel
               2.2.2. Het beeld van een niet-concentrische cirkel
Het gedrag in het oneindige
     3.1. De parabool
     3.2. De hyperbool
     3.3. Evenwijdige lijnen
Duale stellingen
waaronder een projectief bewijs van de stelling van Desargues

1. Definities

Definitie
Onder het projectieve vlak verstaan we het gewone (euclidische) vlak waarbij:
- aan iedere rechte een oneigenlijk punt (een punt op oneindig) is toegevoegd;
- aan het vlak zelf één oneigenlijke rechte (de lijn op oneindig) is toegevoegd.

Op basis van de theorie van "Pool en poollijn" kunnen we nu een afbeelding in het vlak definiëren die de punten van het vlak afbeeldt op de lijnen en de lijnen van het vlak op de punten ervan

Definitie
Een pooltransformatie (ook wel polariteit of polaire afbeelding) is de afbeelding die elk punt van het vlak aan z'n poollijn en elke lijn van het vlak aan z'n pool toevoegt (eea. met betrekking tot een vaste cirkel met middelpunt O).
Aan het oneigenlijke punt van een lijn is toegevoegd de lijn door O loodrecht op die lijn.
Aan de oneigenlijke rechte van het vlak is toegevoegd het punt O.
De vaste cirkel wordt soms inversiecirkel genoemd.

figuur 1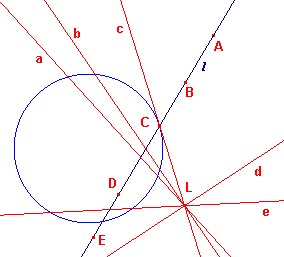

We kunnen ook hier het begrip geconjugeerd vastleggen :

Definitie
De punten A en B heten geconjugeerde punten als A op het beeld van B ligt (en dus ook B op het beeld van A).
De lijnen a en b heten geconjugeerde lijnen als b het beeld van a is (en dus ook als a het beeld is van b).

Opmerking
De beide uitspraken die in de definitie tussen haakjes staan, zijn het gevolg van de Hoofdstelling van de pooltheorie.
[einde Opmerking]

Klik hier voor een animatie van deze afbeelding - punten worden afgebeeld op lijnen
Klik hier voor een animatie van deze afbeelding - lijnen worden afgebeeld op punten

Gevolg
Uit de beide animaties zien we opnieuw:

Lijnen die door een punt gaan worden afgebeeld op punten die op een lijn liggen.
Punten die op een lijn liggen worden afgebeeld op lijnen die door een punt gaan.

[einde Gevolg]

2. Enveloppe, kegelsneden
2.1. De enveloppe als beeld
We vatten nu een kromme lijn K (bijvoorbeeld een cirkel) op als een verzameling punten.
De punten van die kromme worden dus afgebeeld op lijnen. Deze lijnen bevatten elk echter een raakpunt aan een tweede kromme K', de enveloppe van die lijnen.

Afspraak
We zeggen ook wel dat K' het beeld is van K bij een polariteit (zie figuur 2).

figuur 2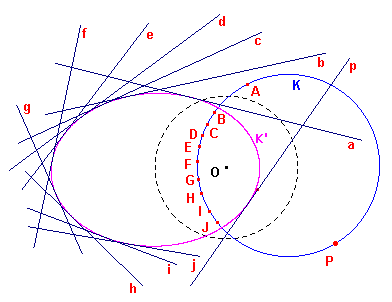

Klik hier voor een animatie van dit type afbeelding.

2.2. Het beeld van een cirkel
2.2.1. Een cirkel concentrisch met de inversiecirkel

figuur 3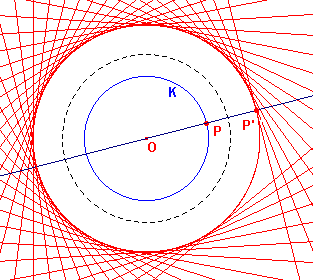

Zie figuur 3
De inversiecirkel heeft middelpunt O en straal r.
De cirkel K heeft eveneens middelpunt O en straal R.
Zij nu P een punt van K.
Het punt P' ligt op OP, zodat
OP . OP' = r²
OP = R, zodat we vinden OP' = r² / R.
Het beeld van K is dus een cirkel K' met middelpunt O en straal r² / R.¨

Klik hier voor een animatie van deze transformatie : punt op enveloppe.
Klik hier voor een animatie van deze transformatie : raaklijn op punt.

2.2.2. Het beeld van een niet-concentrische cirkel

Hulpstelling 1
Zijn A en B punten en a en b lijnen die beeld zijn van A en B bij een polariteit O, dan is
OA / AP = OB / BQ
waarbij AP de afstand is van A tot b en AQ de afstand is van B tot a.

Bewijs: zie figuur 4.

figuur 4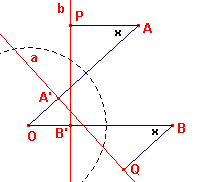

De rechthoekige trapezoïden OAPB' en OBQA' zijn gelijkvormig, immers ze hebben twee hoeken gelijk en uit
   OA . OA' = r² en OB . OB' = r²
volgt
   OA : OB = OB' : OA'.
Dus:
   OA : AP = OB : BQ. ¨

Stelling 1
Het beeld van een cirkel, niet-concentrisch met de inversiecirkel, is een kegelsnede.

Bewijs: zie figuur 5.

figuur 5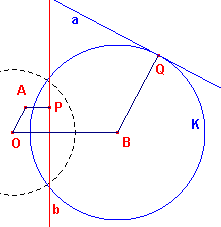

K (middelpunt B en straal R) is een cirkel die niet-concentrisch is met de inversiecirkel.
We vatten nu K op als de enveloppe van de raaklijnen (oa. in Q) aan K.
Het beeld van de raaklijn a in Q bij de polariteit O is het punt A.
Het beeld van B is de lijn b.
Volgens bovenstaande hulpstelling is nu
OA/AP = OB/BQ
OB en BQ = R zijn lijnstukken met een vaste lengte.
Dus
OA / AP = constant
De punten A vormen dus een verzameling waarvoor de verhouding van de afstanden tot een vast punt (O) en tot een vaste lijn (b) constant is.
Die verzameling is een kegelsnede! ¨

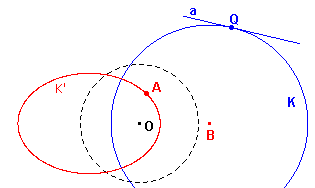
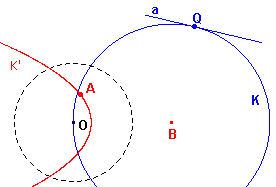
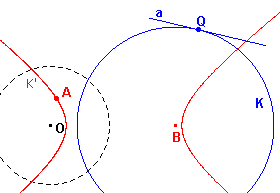
Gevolg
(a) Als OB/BQ < 1, dan is het beeld van K een ellips. Het punt O ligt dan binnen K.
(b) Als OB/BQ = 1, dan is het beeld van K een parabool. Het punt O ligt dan op K
(c) Als OB/BQ > 1, dan is het beeld van K een hyperbool. Het puntO ligt dan buiten K.
Het getal OB/BQ = e heet de excentriciteit van de kegelsnede.

figuur 6a	figuur 6b	figuur 6c

Zie in dit verband ook de pagina "Kegelsneden en hun vergelijkingen".
[einde Gevolg]

Klik hier voor een animatie van het bovenstaande (de punten van de cirkel gaan over in een lijn).
Klik hier voor een animatie van het bovenstaande (de raaklijnen aan de cirkel gaan over in een punt).

3. Het gedrag in het oneindige
Met behulp van de pooltransformatie kunnen we het gedrag van de kegelsneden "in het oneindige" verklaren.
3.1. De parabool
Zie figuur 7.

figuur 7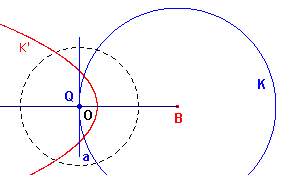

Wanneer het punt Q samenvalt met het punt O, is, per definitie, het beeld van de lijn a het oneigenlijke punt van de lijn OB.
De parabool "raakt" aan de oneigenlijke rechte van het vlak. ¨

Klik hier voor een uiteenzetting mbv. Cabri van deze eigenschap.

Opmerking
Zie ook de pagina "Cabri's FAQ" voor de implementatie van het gebrip "oneindig" in Cabri Geometry II.
[einde Opmerking]

3.2. De Hyperbool
Zie figuur 8.

figuur 8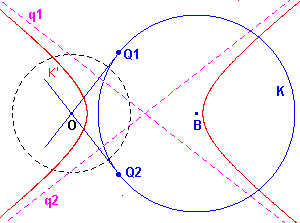

Als a door O gaat, dan ligt O dus op de poollijn van het punt A.
Het punt A ligt dan dus op de poollijn van O, en dat is de oneigenlijke rechte. A ligt dus "in het oneindige".
Er zijn twee posities van het punt Q waarin dit het geval is (de raakpunten Q₁ en Q₂ van de raaklijnen uit O aan de cirkel K).
De hyperbool snijdt de oneigenlijke rechte van het vlak dus in twee punten.¨

De beelden q₁ en q₂ van de punten Q₁ en Q₂ zijn de asymptoten van de hyperbool.

3.3. Evenwijdige lijnen
We kunnen het gedrag in het oneindige van evenwijdige lijnen ook fraai met behulp van pooltransformaties onderzoeken.
We vragen ons dus af wat er gebeurt als we (de punten van) twee evenwijdige lijnen aan een pooltransformatie onderwerpen.
Zie figuur 9.

figuur 9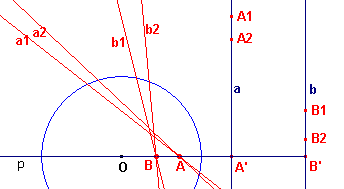

De lijnen a en b zijn evenwijdig.
Alle punten van a worden afgebeeld op lijnen door het punt A (het beeld van a ten opzichte van O).
Alle punten van b worden afgebeeld op lijnen door het punt B (het beeld van b ten opzichte van O).
En dus ook omgekeerd: alle lijnen door A (en B) worden afgebeeld op punten van a (en b).
Maar ook de lijn p door O loodrecht op a en b is een lijn door A en door B.

Het punt O ligt op p.
Dus: het beeld P van p ligt op het beeld O, dwz. dat P op de oneigenlijke rechte van het vlak ligt.
Maar ook:
- A ligt op het beeld van P, dus P ligt op het beeld van A, dwz op a.
- B ligt op het beeld van P, dus P ligt op het beeld van B, dwz. op b. ¨
Dus hebben we

Stelling 2.1
Twee evenwijdige rechten hebben hetzelfde oneigenlijk punt
OF ook
Twee evenwijdige lijnen snijden elkaar op de oneigenlijke rechte van het vlak.

We kunnen uit het bovenstaande bewijs ook gemakkelijk afleiden:

Stelling 2.2
Een polariteit O beeldt evenwijdige lijnen af op punten die collineair zijn met het punt O,
en, omgekeerd,
punten die collineair zijn met het punt O worden afgebeeld op evenwijdige lijnen.

Klik hier voor een animatie van het tweede deel van stelling 2.2.

Opmerkingen
[1]
We zullen stelling 2.2 hieronder in stelling 4 gebruiken bij het ("projectieve") bewijs van de stelling van Desargues.
[2]
Zie ook de pagina "Cabri's FAQ" voor de implementatie van het begrip "oneigenlijke rechte" in Cabri Geometry II.
[einde Opmerkingen]

4. Duale stellingen
We kunnen via pooltransformatie uit stelling die iets zeggen over punten (lijnen) nieuwe stellingen afleiden die iets zeggen over lijnen (punten).
Deze afgeleide stellingen heten duale stellingen.
Duale stellingen ontstaan in het algemeen door elementen (punten, lijnen, .....) te onderwerpen aan een projectieve transformatie. De duale stelling zegt dan iets over de beelden van die elementen.
Duale stellingen in deze paragraaf zijn daardoor het Gevolg van de definitie van pooltransformaties.

Hulpstelling 2
Zijn A en B de polen van twee lijnen a en b bij een pooltransformatie O, dan is Ð AOB = Ð (a,b).

Bewijs: zie figuur 10.

figuur 10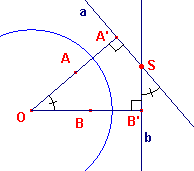

Vierhoek OA'SB' is een koordenvierhoek.Waaruit de gelijkheid van de hoeken onmiddellijk volgt. ¨

We kunnen deze eigenschap gebruiken in het bewijs van de volgende stelling(en).

Stelling 3
Liggen de punten A en B op een cirkel en is AB middellijn van die cirkel, dan is hoek C recht.
Duaal:
Snijden twee evenwijdige raaklijnen aan een cirkel met middelpunt O een derde raaklijn in de punten P en Q, dan is hoek POQ een rechte hoek.

Bewijs: zie figuur 11.

figuur 11 :

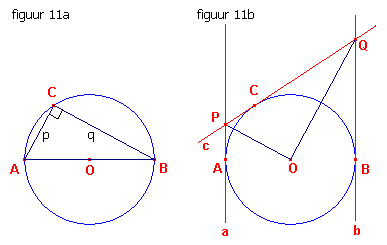In figuur 11a staat de Stelling van Thales voor cirkels: hoek ACB is recht.
Passen we nu de pooltransformatie O toe, dan gaan de punten A,B,C over in de raaklijnen a,b,c.
Het beeld van p is het punt P, het beeld van q is het punt Q.
Volgens Hulpstelling 2 is nu
ÐPOQ = Ð(p,q) = 90º ¨

Hulpstelling 3
Bij een pooltransformatie worden drie collineaire punten afgebeeld op drie concurrente lijnen en omgekeerd.

Bewijs: zie figuur 12

figuur 12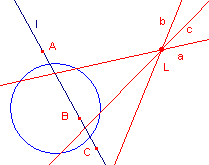

Het bewijs volgt direct uit de pool-poollijn eigenschap.
De lijn l wordt door de transformatie afgebeeld op een punt L (de pool van L).
A ligt op de poollijn van L, dus L ligt op de poollijn van A; enz. ¨

Met behulp van Hulpstelling 3 kunnen we de Stelling van Desargues (Girard Desargues, 1593-1662, Frankrijk) bewijzen. Een bewijs gebaseerd op de Stelling van Menelaos staat op de pagina "Transversalen" in Paragraaf 7.4.

Stelling 4 - Stelling van Desargues
Twee driehoeken die punt-perspectief zijn, zijn ook lijn-perspectief (en omgekeerd)

Bewijs: zie figuur 13.

figuur 13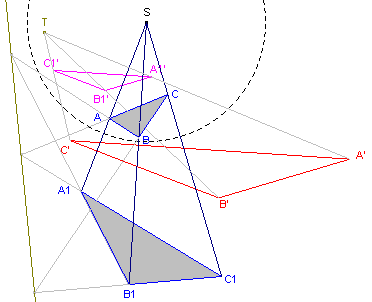

Zijn ABC en A₁B₁C₁ twee driehoeken die punt-perspectief zijn tov. het punt S.
We kiezen nu de polariteit met S als centrum.
Hierdoor gaan de driehoeken over in de driehoeken A'B'C en A₁'B₁'C₁'.
Deze driehoeken hebben echter een bijzonderheid:
de overeenkomstige zijden zijn evenwijdig.
Dit kan eenvoudig worden afgeleid uit Stelling 2.2 (toegepast op S,A,A1; enz.).
Deze driehoeken liggen homothetisch (of kunnen in een bijzonder geval via een trabslatie op elkaar worden afgebeeld).
De verbindingslijnen van overeenkomstige hoekpuntenzijn dus concurrent (eventueel in een oneigenlijk punt).
Zie hiervoor het punt T in figuur 13.
Deze drie verbindingslijnen worden nu afgebeeld op drie punten die collineair zijn (volgens Hulpstelling 3).

De collineatie-as is de poollijn van het punt T.
De genoemde punten zijn echter ook de snijpunten van de overeenkomsige zijden van de driehoeken ABC en A₁B₁C₁.
Er is dus sprake van lijn-symmetrische ligging van de beide driehoeken.
Omgekeerd.
We passen een willekeurige polariteit toe op het diagram in figuur 13. Hierdoor worden de driehoeken ABC, A₁B₁C₁ afgebeeld op beelddriehoeken die de pool van de collineatieas als centrum van de punt-perspectiviteit hebben. ¨

Opmerking
De duale stelling bij de stelling van Desargues is dus de

Stelling 4 duaal
De overeenkomstige zijden van homothetische driehoeken (of driehoeken waartussen een translatie-verband bestaat) zijn evenwijdig

Klik hier voor een animatie van het bovenstaande waarbij uitgegaan wordt van twee homothetische driehoeken die door een polariteit worden afgebeeld op twee lijn-perspectieve driehoeken.

[einde Opmerking]

Stelling 5
De zwaartelijnen van een driehoek zijn concurrent.
Duaal: ....

Onderstaand volgt de formulering van de duale stelling van Stelling 5. Zie daartoe eerst figuur 14 en figuur 15.

figuur 14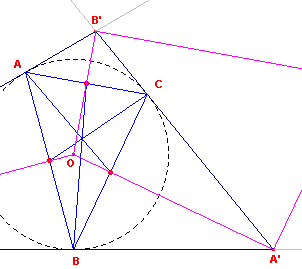

We kiezen als inversiecirkel de omcirkel van driehoek ABC met middelpunt O.
Driehoek ABC gaat bij de polariteit O over in de raaklijnendriehoek A'B'C'.
De middens van de zijden gaan over in lijnen door de punten A',B',C'.
Deze lijnen staan echter loodrecht op de binnenbissectrices van A'B'C', immers OA' ^ BC, OB' ^ AC, OC' ^ AB.
De beelden van de zwaartelijnen zijn dus de buitenbissectrices van driehoek A'B'C.
De zwaartelijnen van ABC gaan door één punt.
De beelden van de zwaartelijnen zijn dus collineair op de beeldlijn van het zwaartepunt.
Dit zijn tevens de punten waarin de buitenbissectrices de overstaande zijden van A'B'C' snijden. ¨
Dus:

figuur 15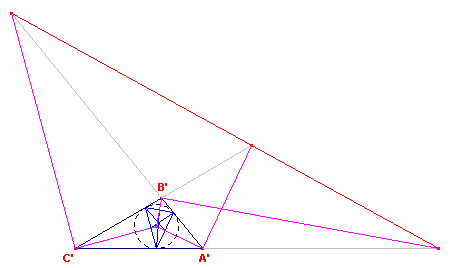

Stelling 5 duaal
De snijpunten van de buitenbissectrices van een driehoek met de overstaande zijden zijn collineair.

Stelling 6
De hoogtelijnen van een driehoek zijn concurrent.
Duaal: .....

Zie figuur 16 voor de duale formulering.

figuur 16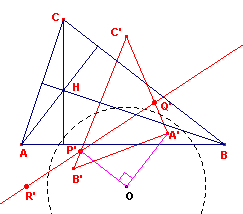

Onder de wilekeurige polariteit met centrum O gaat driehoek ABC over in een driezijde bepaald door de punten A',B',C'.
De hoogtelijnen gaan over in de punten P', Q', R' die collineair zijn. Daarbij liggen deze punten zo op de zijden van driehoek A'B'C' dat
ÐA'OP' = ÐB'OQ' = ÐC'OR'=90º. ¨
Dus:

Stelling 6 duaal
De snijpunten van de lijnen door O loodrecht op OA', OB', OC' met de zijden van de overeenkomstige zijden van A'B'C' zijn collineair.

Klik hier voor een animatie van stelling 6 duaal.

[pooltrans.htm] laatste wijziging op: 12-12-2003