Pool en poollijn ten opzichte van een cirkel

Overzicht  ][  Meetkunde

Zie ook de pagina "Pooltransformatie"
Zie ook het Cabri-werkblad "Pool en poollijn bij een cirkel"

0. Overzicht

  1. Definities cabrisignal
  2. Hoofdstelling van de pooltheorie cabrisignal
  3. Geconjugeerde punten en harmonische ligging
  4. Constructie
         4.1. Gebruik van de volledige vierhoek
         4.2. Liniaalconstructie cabrisignal
  5. Enkele stellingen waaronder cabrisignal
         Stelling van Chasles
         Stelling van Hesse
  6. Meer over geconjugeerde driehoeken

1. Definities
Uitgaande van de inversie ten opzichte van een cirkel kunnen we definiëren

Definitie
Twee punten P en P' zijn toegevoegd ten opzichte van een cirkel met middelpunt O en straal r, als
   OP . OP' = r2
waarbij O, P, P' op dezelfde rechte lijn liggen.

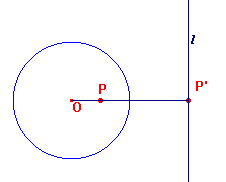
Op basis hiervan leggen we vervolgens een afbeelding F vast van de punten van het (uitgebreide) vlak op de lijnen van dat vlak (zie figuur 1):

figuur 1  pool1 F(P) = l voor P niet samenvallend met O; hierbij is l de lijn in P' loodrecht op OP.
F(O) = de oneigenlijke rechte van het vlak.
 
Definitie
l heet de poollijn (eng. polar) van P tov. de cirkel; P heet de pool (Eng. pole) van l tov. de cirkel.

De inverse functie van F beeldt dan de verzameling lijnen weer af op de verzameling punten in het (uitgebreide) vlak.

Klik hier Animatie voor een animatie van deze definitie.

2. Hoofdstelling van de pooltheorie

Stelling 1 (hoofdstelling van de pooltheorie)
Als Q op de poollijn van P ligt, dan ligt P op de poollijn van Q (ten opzichte van dezelfde cirkel).

Bewijs: zie figuur 2.

figuur 2  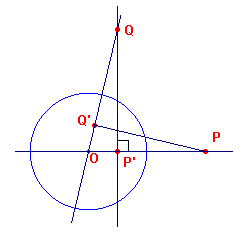pool2 P, P' en Q, Q' zijn toegevoegde punten ten opzichte van cirkel O met straal r.
Nu geldt
   OP . OP' = r2
   OQ . OQ' = r2
Daaruit volgt dat OP : OQ = OQ' : OP'
waaruit weer volgt dat driehoek OPQ' ~ driehoek OQP' (zhz)
(of ook: uit de gelijkheid van de producten volgt dat P'PQQ' is een koordenvierhoek).
Dus de hoek bij Q' is recht.
PQ' is dus de poollijn van Q (en P ligt daarop). ¨

Klik hier Animatie voor een animatie van de hoofdstelling
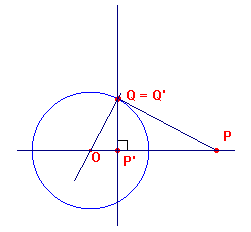figuur 3  pool3 Gevolg
De poollijn van een punt P buiten de cirkel gaat door de raakpunten uit P aan die cirkel (zie figuur 3).
[einde Gevolg]

N.b.
De hoofdstelling van de pooltheorie staat ook wel bekend als de Stelling van De la Hire (naar Philippe de la Hire, 1640-1718, Frankrijk).

Opmerking
Deze hoofdstelling van de pooltheorie wordt oa. gebruikt bij de algemene oplossing van het Raakprobleem van Apollonius (constructie van de raakcirkels aan drie gegeven cirkels).
[einde Opmerking]

3. Geconjugeerde punten en harmonische ligging

Definitie
Twee punten zo gelegen, dat het ene punt ligt op de poollijn van de andere tov. een gegeven cirkel heten geconjugeerde punten tov. de cirkel.
Twee lijnen zo gelegen, dat de ene lijn gaat door de pool van de andere lijn tov. een gegeven cirkel heten geconjugeerde lijnen tov. die cirkel.

We geven allereerst een stelling over hamonische ligging van punten (zie ook paragraaf 3.2 op de pagina "Dubbelverhouding")

Stelling 2
Zijn P en P' toegevoegde punten tov. van een cirkel met middelpunt O, dan worden P en P' harmonisch gescheiden door de snijpunten  van OP en de cirkel.

Bewijs: zie figuur 4.

figuur 4  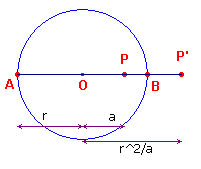pool4 Zijn A en B de snijpunten van de lijn OP met de cirkel.
Nu is
(ABPP') = PA/PB : P'A/P'B
   = - (r + a) / (r - a) : (r2/a + r) / (r2/a - r)
   = - (r + a) / (r - a) : (r + a) / (r - a)
   = -1 ¨

Een direct gevolg van deze stelling is dan
  
Stelling 3.1
Als bij een gegeven cirkel, twee geconjugeerde punten op een lijn liggen die de cirkel snijdt, dan worden deze punten door de snijpunten van die lijn met de cirkel harmonisch gescheiden.

Bewijs: zie figuur 5a.

figuur 5a  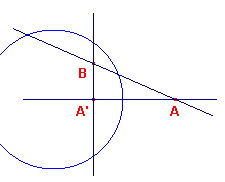pool5 Zijn A en B geconjugeerde punten, en is A' de inverse van A tov. de cirkel.
Als B = A', dan volgt de stelling onmiddellijk uit Stelling 2.
Valt B niet samen met A', dan is BA' de poollijn van A.
De Thales-cirkel met BA als middellijn snijdt dan de gegeven cirkel loodrecht.
Volgens de eerste stelling uit paragraaf 4, pagina "Vierzijde", scheiden de punten elkaar harmonsich. ¨
  
Gevolg van Stelling 3.1
Als een variabele lijn door een gegeven punt een cirkel snijdt, dan liggen de harmonisch toegevoegden van dat punt met betrekking tot de snijpunten van die lijn en de cirkel, op de poollijn van het punt.
 
Stelling 3.2
Zijn a en b twee geconjugeerde lijnen ten opzichte van een cirkel, die elkaar buiten de cirkel snijden, dan worden a en b  harmonisch gescheiden door de raaklijnen uit dat snijpunt aan de cirkel.

Bewijs: zie figuur 5b.

figuur 5b  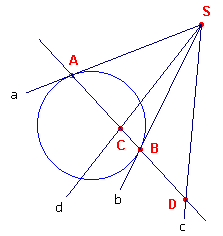pool5b In deze figuur zijn C en D geconjugeerde punten. C ligt op de poollijn d van D; D ligt op de poollijn c van D.
De lijn CD is dus de poollijn van het snijpunt S van c en d.
Zijn SA en SB raaklijnen uit S aan de cirkel dan is dus volgens stelling 3.1:
   (ABCD) = -1.
Volgens de definitie van de dubbelverhouding bij lijnen hebben we dus ook:
   (abdc) = -1
¨

We kunnen eenvoudig aantonen, dat de dubbelverhouding van vier punten op een rechte wordt overgebracht op de dubbelverhouding van de poollijnen van die punten ten opzichte van een cirkel.

 
Stelling 3.3
Voor de punten A, B, C, D met poollijnen a, b, c, d geldt (ABCD) = (abcd).

Bewijs: zie figuur 5c.

figuur 5c  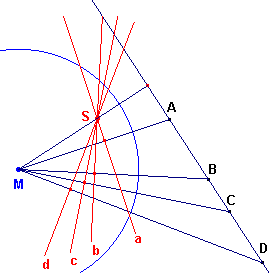pool5c De poollijnen van de punten gaan alle door het punt S.
Omdat elke poollijn loodrecht staat op de verbindingslijn van zijn pool met het middelpunt van de cirkel, vinden we
   (abcd) = M(ABCD) = (ABCD). ¨

4. Constructie

4.1. Gebruik van de volledige vierhoek
We hebben nu de volgende interessante

Stelling 4
Is ABCD een volledige vierhoek beschreven in een cirkel, dan is elk diagonaalpunt van de vierhoek de pool van de lijn bepaald door de beide andere diagonaalpunten.

Bewijs: zie figuur 6.

figuur 6  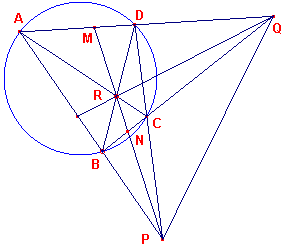pool6 We hebben in deze figuur
   (ADMQ) = (BCNQ) = -1 (eigenschap van een volledige vierhoek)
Dus lijn PR (= MN) is de poollijn van het punt Q (zie Gevolg bij Stelling 3).
Op dezelfde manier vinden we dat QR de poollijn is van van het punt P.
Dus, volgens de hoofdstelling, is PQ de poollijn van het punt R. ¨

Gevolg
Op basis van deze stelling kunnen we de poollijn van een punt alleen met gebruik van een liniaal construeren (zie Liniaalconstructie), gegeven de cirkel.

Opmerking
Op grond van de definitie van zelfgeconjugeerd zijn (zie hieronder) is driehoek PQR zelfgeconjugeerd.
[einde Opmerking]

4.2. Liniaalconstructie
Zie hiervoor figuur 6.
We geven onderstaand de stappen voor de constructie van de poollijn van P ten opzichte van de cirkel.

1.     Teken twee lijnen door P die de cirkel snijden.
2.    Bepaal de snijpunten A, B en C, D van deze lijnen met de cirkel..
3.    Trek AD, BC met snijpunt Q.
4.    Trek AC, BD met snijpunt R.
5.    Trek QR.
 QR is dan de gewenste poollijn.

Klik hier Animatie voor een animatie van deze constructie.

5. Enkele andere stellingen

Definitie
De cirkel met het machtpunt van drie cirkels als middelpunt die de drie cirkels loodrecht snijdt, heet machtcirkel van die drie cirkels.
 
Stelling 5
Is K een punt van de machtcirkel van drie cirkels, dan zijn de poollijnen van K ten opzichte van die drie cirkels concurrent (in een punt van de machtcirkel)

Bewijs: zie figuur 7.

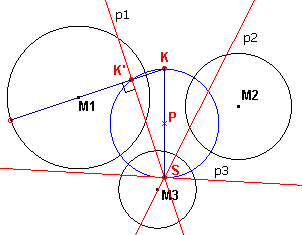figuur 7  pool7 De cirkel met middelpunt P is de machtcirkel van M1, M2, M3.
p1, p2, p3 zijn de poollijnen van K ten opzichte van M1, M2, M3.
We zullen nu aantonen, dat p1, p2, p3 concurrent zijn in het punt S.
K' is de inverse van K ten opzichte van de cirkel  M1. Omdat deze de machtcirkel loodrecht snijdt, geldt K' ook op de machtcirkel ligt (zie de eigenschap over harmonische ligging en loodrechte cirkels op de pagina "Vierzijde").
p1 snijdt de machtcirkel in het punt S. Nu is S het tegenpunt van K op de machtcirkel, omdat hoek KK'S recht is.
De poollijn van het punt K (ic. p1) van de machtcirkel gaat dus door het tegenpunt van dat punt (ic. het punt S).
Dit geldt dus ook voor p2 en p3. ¨

Klik hier Animatie voor een animatie van deze stelling.

Definities
Twee driehoeken heten geconjugeerd (ten opzichte van een cirkel) als de hoekpunten van de ene driehoek de polen zijn van de zijden van de andere driehoek.
Een driehoek heet zelfgeconjugeerd (tov. een cirkel) als elk hoekpunt de pool is van de overstaande zijde.
Een zelfgeconjugeerde driehoek heet ook wel pooldriehoek van de cirkel.

Voor geconjugeerde driehoeken hebben we nu een stelling die in de projectieve meetkunde bekend staat als de Stelling van Chasles (Michel Chasles, 1793-1880, Frankrijk) :

Stelling 6
Twee geconjugeerde driehoeken zijn puntperspectief (ook wel copolair ; dwz. AA', BB', CC' zijn concurrent).

Bewijs: zie figuur 8a.

figuur 8a  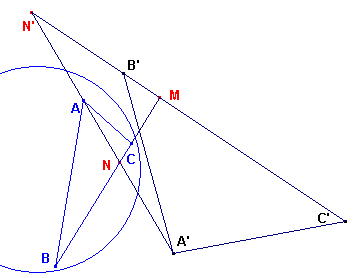pool8 In de figuur zijn ABC en A'B'C' twee geconjugeerde driehoeken.
BC snijdt C'C' in het punt M.
AA' snijdt BC in N en B'C' in N'.
N ligt op BC, de poollijn van A', dus A' ligt op de poollijn van N.
M ligt op BC, de poollijn van A'.
M ligt op B'C', de poollijn van A.
AA' is dus de poollijn van M.
N ligt op BC, de poollijn van A'.
N ligt op AA', de poollijn van M.
A'M is dus de poollijn van N
Nu is
   (BCNM) = (volgens stelling 3.3)
   = A'(C'B'MA) = A'(C'B'MN') = (C'B'MN') = (verwisseling)
   = (B'C'N'M)

Aangezien in de dubbelverhoudingen (BCNM) en (B'C'N'M) het punt M invariant is, geldt: BB', CC', NN' (= AA') zijn concurrent (zie hiervoor ook (hulp)figuur 8b). ¨

figuur 8b  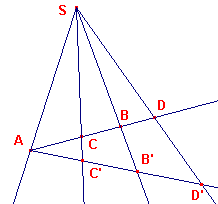pool5d In nevenstaande figuur geldt (ABCD)=(AB'C'D').
De lijnen BB', CC', DD' zijn concurrent.

Opmerking
Volgens de stelling van Desargues zijn de driehoeken in Stelling 6 dus ook lijnperspectief (ook wel coaxiaal).
We gebruiken deze eigenschap in Stelling 7.
[einde Opmerking]
 
Stelling 7 - Stelling van Hesse voor cirkels
Als twee paren van overstaande hoekpunten van een volledige vierzijde geconjugeerd zijn tov een cirkel, dan is ook het derde paar geconjugeerd.
Ludwig Hesse (1811-1874, Duitsland) publiceerde deze stelling in 1840.

Bewijs: zie figuur 9.

figuur 9  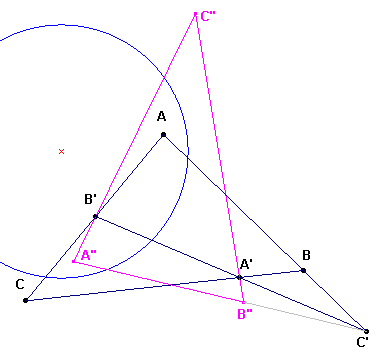pool9 In de figuur is AB'A'B een vierhoek die de volledige vierzijde bepaalt. De beide andere hoekpunten van de vierzijde zijn C en C'.
De paren A, A' en B,B' zijn geconjugeerde punten tov. de cirkel.
Zij nu A"B"C" de geconjugeerde driehoek van ABC.
B"C" gaat dan door A'.
A"C" gaat dan door B'.
Echter ABC em A"B"C" zijn geconjugeerd, dus zijn ze ook lijnperspectief (zie de Opmerking bij Stelling 6).
De snijpunten van de paren overeenkomstige zijden (AB, A"B"), (BC, B"C") en (CA, C"A") zijn dus collineair.
De laatste twee van deze snijpunten zijn A' en B'.
Het derpunt is dus noodzakelijk C'.
Dat wil zeggen, dat A"B" door C' gaat, zodat C en C' eveneens geconjugeerde punten tov. de cirkel zijn ¨ .

Opmerking
De stelling van Hesse blijft geldig, als het geconjugeerd zijn wordt vastgelegd ten opzichte van een kegelsnede.
Zie bijvoorbeeld ook de Stelling van Pascal en de Stelling van Brianchon.
[einde Opmerking]

6. Meer over geconjugeerde driehoeken
Klik hier voor enkele andere eigenschappen van geconjugeerde driehoeken, en meer in het bijzonder van zelfgeconjugeerde driehoeken

up
[pool.htm] laatste wijziging op: 07-12-2005