De stellingen van Pascal en Brianchon voor cirkels
Overzicht ][ Transversalen | Meetkunde
1. De Stelling van Pascal voor cirkels
![]()
De stelling van Pascal (Blaise Pascal, 1623-1662, Frankrijk), geformuleerd voor
cirkels, luidt
| Stelling van Pascal voor cirkels Van een zeshoek (niet noodzakelijk convex) waarvan de hoekpunten op een cirkel liggen, zijn de snijpunten van de drie paren overstaande zijden verschillend en collineair. |
Bewijs: zie figuur 1.
| figuur 1 | 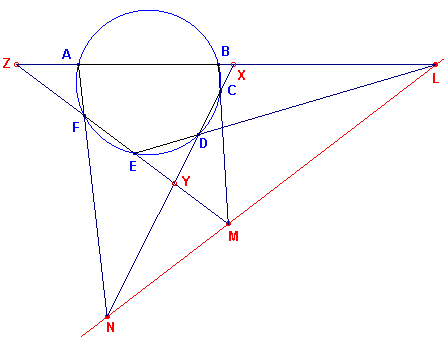 |
ABCDEF is een zeshoek die een omgeschreven cirkel heeft.
De snijpunten van de paren overstaande zijden (AB, DE), (BC, EF), (CD, FA) zijn opvolgend
L,M,N.
Nu zijn L,M,N collineair.
Stel X = (AB,CD), Y = (CD,EF) en Z = (EF,AB).
Beschouw nu driehoek XYZ met transversalen DE, FA en BC.
Volgens de Stelling van Menelaos geldt nu (voor elk drietal
punten op de zijden)
(XZL)(ZYE)(YXD) = 1
(XZA)(ZYF)(YXN) = 1
(XZB)(ZYM)(YXC) = 1
Vermenigvuldiging van deze uitdrukkingen geeft na ordening
![]()
Zodat, wegens AX·BX = DX·CX, enz (cirkeleigenschap):¶
(XZL)(ZYM)(YXN) = 1
En wederom volgens de (omgekeerde) Stelling van Menelaos:
L,M,N zijn collineair. ¨
Klik hier ![]() voor een animatie van de Stelling van Pascal.
voor een animatie van de Stelling van Pascal.
Opmerkingen
[1]
Er is ook een bewijs mogelijk gebaseerd op koordenvierhoeken
en omtrekshoeken met de stelling van Miquel als uitgangspunt.
Klik hier voor het downloaden
van een geZIPt Word-document met dit bewijs [ca. 34kB].
[2]
Er zijn 5!/2 = 60 manieren om uit 6 punten een zeshoek op de cirkel te kiezen (begin
steeds bij 1; dan zijn er 5! manieren waarop de overige 5 hoekpunten kunnen worden
gepermuteerd; maar 123456 = 165432; dus 5!/2 is het aantal verschillende).
Bij elk van deze mogelijkheden hoort een Pascal-lijn. We hebben dus 60
verschillende Pascal-lijnen.
Deze lijnen gaan drie bij drie door 20 punten: Steiner-punten, die weer vier bij
vier op 15 lijnen liggen: Plücker-lijnen.
De Pascal-lijnen gaan ook drie bij drie door een tweede verzameling bestaande uit 60
punten: Kirkman-punten.
Er bestaat een duale relatie tussen de 60 Pascal-lijnen en de 60 Kirkman-punten.
Met elk Steiner-punt komen drie Kirkman-punten overeen, en wel zo, dat deze vier weer op
een rechte lijn liggen: Cayley-lijnen.
Er zijn 20 Cayley-lijnen die vier bij vier door 15 punten gaan: Salmon-punten.
Heronder (in figuur 2) zijn enkele van de Pascal-lijnen (lijnen door a1a2a3, b1b2b3, ......),
Steiner-punten bijv. a2=d2=g2), een Kirkman-punt (K) en drie Cayley-lijnen (de
lijnen door K) getekend.
| figuur 2 | 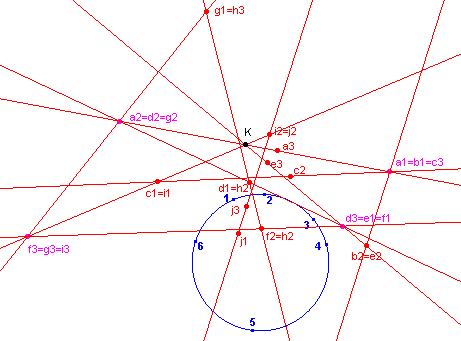 |
De gebruikte zeshoeken hierbij zijn: a = 123456 b =123546 c =134562 d =165423 e =132546 f = 136452 g =156432 h =163425 i = 134652 j = 152634 |
[einde Opmerkingen]
2. De stelling van
Pappos ![]()
Zoals elders ook is opgemerkt (op de pagina Transversalen),
is de stelling van Pascal ook geldig voor een kegelsnede (en cirkel is een bijzondere
kegelsnede, nl. een ellips met gelijke assen).
Indien echter de kegelsnede ontaardt in twee rechte lijnen, dan blijft de stelling ook
geldig.
Deze stelling is reeds door Pappos (Pappos van Alexandrië, 300 nC, Egypte) geformuleerd:
| Stelling van Pappos Als van een zeshoek de hoekpunten afwisselend liggen op twee rechte lijnen, dan zijn de snijpunten van overstaande zijden collineair. |
| figuur 3 |  |
Klik hier Klik hier voor een PDF-bestand (ca. 122 kB) met een bewijs van de Stellling van Pappos. |
Opmerking
Ook de stelling van Pappos speelt een rol in de axiomatische opbouw van de (projective)
meetkunde
[einde Opmerkingen]
3. De stelling van Brianchon voor
cirkels ![]()
De stelling is inderdaad in 1806 ontdekt door Brianchon (Charles Julien Brianchon, 1785-1864, Frankrijk), meer
dan 150 jaar nadat Pascal zijn beroemde zeshoeksstelling formuleerde.
| Stelling van Brianchon Als een zeshoek een zeshoek (niet noodzakelijk convex) om een cirkel beschreven is, dan zijn de drie lijnen die de overstaande hoekpunten verbinden, concurrent. |
Bewijs: zie figuur 4.
| figuur 3 | 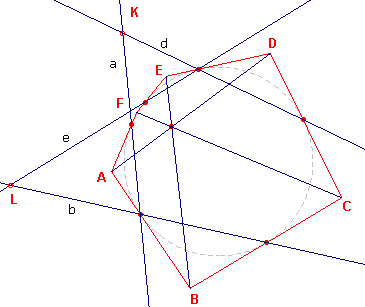 |
De lijn a is de poollijn van A; de lijn d is de poollijn van D. K is dan de pool van AD. De lijn b is de poollijn van B; de lijn e is de poollijn van E L is dan de pool van BE. Evenzo is er een punt M, dat de pool is van CF. De poollijnen zijn de overstaande zijden van de zeshoek die de raakpunten als hoekputen heeft. Volgens de stelling van Pascal zijn de punten K,L,M dan collineair. Deze collineatie-as heeft een pool O ten opzichte van de cirkel. K, L, M liggen op de poollijn van O. O ligt dan op de poollijnen van K,L,M (AD, BE, CF), volgens de hoofdstelling van de pooltheorie. De drie lijnen gaan dus door één punt. ¨ |
Klik hier ![]() voor een animatie van de Stelling van Brianchon.
voor een animatie van de Stelling van Brianchon.
Opmerkingen
[1]
Evenals de stelling van Pascal, kan de stelling van Brianchon ook geformuleerd worden voor
een kegelsnede. Het bewijs kan dan met middelen uit de projectieve meetkunde worden
geleverd.
[2]
In de projectieve meetkunde is er sprake van dualiteit tussen de begrippen
("punt", "lijn"), ("gaan door", "liggen op"),
("concurrent, collineair").
Daarnaast kunnen we een kegelsneden (of andere kromme lijn) enerzijds opvatten als een
verzameling punten, anderzijds als de omhullende (envelop) van de raaklijnen. We kunnen
dan spreken van een punt-kegelsnede of een lijn-kegelsnede.
Vergelijk beide formuleringen:
| Stelling van Pascal Als de zes punten 1,2,3,4,5,6 liggen op een punt-kegelsnede, dan zijn de punten bepaald door de paren lijnen (12 ; 45), (23 ; 56) en (34 ; 61) collineair. Duale stelling van Pascal Als de zes lijnen 1,2,3,4,5,6 liggen op een lijn-kegelsnede, dan zijn de lijnen bepaald door de paren punten (12 ; 45), (23 ; 56) en (34 ; 61) concurrent. |
We zien dus dat de duale stelling van Pascal overeenkomt met de stelling van Brianchon.
[3]
Raaklijnenvierhoek, raaklijnendriehoek (punt van Gergonne)
Bijzondere gevallen van de stelling van Brianchon vinden we als we
enkele raakpunten laten samenvallen; zie figuur 4.
| figuur 4a | 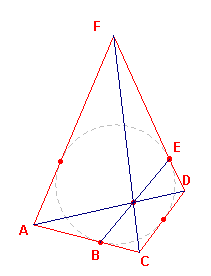 |
figuur 4b | 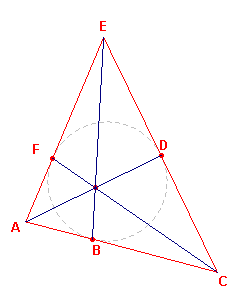 |
In figuur 4a zien we een raaklijnenvierhoek. Deze is ontstaan uit de
zeshoek (van Brianchon) door de punten B en E op de cirkel te kiezen.
In figuur 4b is dat zelfde gedaan met de punten B, D en F.
Hieruit zien we onmiddellijk, dat de verbindingslijnen van de hoekpunten met het raakpunt
van de incirkel op de overstaande zijde concurrent zijn.
Het punt is het punt van Gergonne (zie ook paragraaf
4.5 op de pagina "Transversalen" en ook de
pagina "Gergonne-punt").
[4]
De stelling van Brianchon kan in de hyperbolische meetkunde
worden gebruikt om aan te tonen, dat de bissectrices van een driehoek concurrent zijn.
Zie daarvoor de pagina "Hyperbolische meetkunde
[4], Lengte van lijnstukken".
[einde Opmerkingen]
[pascal.htm] laatste wijziging op: 28-12-2004