Maantjes van Hippocrates

Inleiding | Maantjes | PDF ][ Elementen | Meetkunde | Cabri

1. Inleiding
Eén van de oud-Griekse wiskundige problemen staat bekend onder de naam Kwadratuur van de cirkel; dat is het construeren (met passer en liniaal) van een vierkant waarvan de oppervlakte gelijk is aan die van een gegeven cirkel (het construeren wordt in dit verband wel kwadreren genoemd).
We weten sinds 1882 (Ferdinand von Lindemann, 1852-1939) dat dit probleem onoplosbaar is (zie ook de pagina "Over de trisectie van een hoek").

Hippocrates van Chios (470-410 vChr, Griekenland) vond een methode om de oppervlakte van bijzondere kromlijnige figuren, namelijk maantjes, te kwadreren.

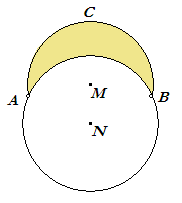Definitie
Een maantje is een figuur die wordt begrensd door twee cirkelbogen.

2. Maantjes van Hippocrates
De door Hippocrates gevonden methode is gebaseerd op de zogenoemde uitgebreide stelling van Pythagoras (zie de pagina "Boek VI", Elementen van Euclides):

Propositie VI-31
In rechthoekige driehoeken is [de oppervlakte van] een figuur, beschreven op de den rechten hoek onderspannende zijde, gelijk aan [de som van de oppervlaktes van] de op de den rechten hoek omvattende zijden op gelijke wijze beschreven gelijkvormige figuren.

Voor de gelijkvormige figuren worden dan halve cirkels gebruikt. In onderstaande figuur wordt dit geïllustreerd. De maantjes ontstaan daarbij als 'doorsnedes' van de halve cirkel op de schuine zijde van de rechthoekige driehoek met die op de beide rechthoekszijden.
We geven de oppervlakte van een maantje aan met 'luna'; die van een cirkelsegment / cirkelsector met 'segment' / 'sector'.

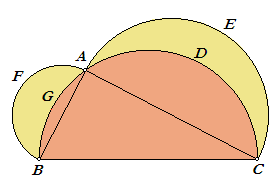Een bewijs:
Volgens Prop. VI-31 is hier:
sector(BAF) + sector(ACE) = sector(BCA)
Trekken we links en rechts van het gelijkteken de waarde van segment(BAG) + segment(ACD) af, dan vinden we:
luna(BGAF) + luna(ADCE) = oppervlakte(driehoek ABC)

En hieruit blijkt dan dat we de som van de oppervlakte van beide maantjes kunnen kwadreren.

Klik hier >< voor een applet waarin het bovenstaande wordt geïllustreerd. Hierbij is het noodzakelijk dat de Cabri Plug-in op het systeem is geïnstalleerd.

We kunnen een en ander ook op een iets andere manier bekijken.

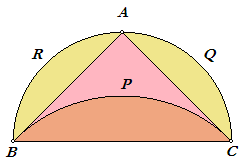Op de zijden AB, BC en CA van een gelijkzijdige in A rechthoekige driehoek ABC zijn sectoren BAR, BCP en ACQ geplaatst, en wel zo, dat ze gelijkvormig zijn.
Dan geldt, eveneens volgens Prop. VI-31:
segment(BAR) + segment(ACQ) = segment(BCP)
Tellen we aan beide kanten van het gelijkteken de oppervlakte van het driehoekige, deels kromlijnige, vlakdeel BPCA erbij op, dan vinden we:
luna(BPCA) = oppervlakte(driehoek ABC)

En ook nu zien we dat we een maantje, en hier is dat BPCQAR, kunnen kwadreren.

3. PDF
Een PDF-bestand waarin uitvoerig wordt ingegaan op construeerbare maantjes is beschikbaar via deze website (artikel: Kwadreerbare maantjes).
Klik hier om dat bestand te downloaden (17 pagina's A4; grootte: 251Kb).

[p: pytha/maantjes.htm] laatste wijziging op: 13-01-2008