Commentaar van Proclus op Propositie I-47 (Euclides: Elementen)
Overzicht ][ Pythagoras | Elementen | Meetkunde
Zie ook de pagina "Boek VI"
1. Proclus' commentaar
![]()
Vertaling uit het Grieks:
Glen R. Morrow in Proclus: A Commentary on the First Book of Euclid's Elements
(Princeton University Press, 1970; herdruk 1992)
[Zie verder ook History of Mathematics: Proclus (411-485)]
[...]
If we listen to those who like to record antiquities, we shall
find them attributing this theorem to Pythagoras and saying that he sacrificed an ox on
its discovery. For my part, though I marvel at those who first noticed the truth of this
theorem, I admire more the author of the Elements, not only for his lucid proof by which
he made it fast, but also because in the sixth book he laid hold of a theorem even more
general then this and secured it by irrefutable scientific arguments. For in that book he
proofs generally that in right angled triangles the figure on the side that subtends the
right angle is equal to the similar and similarly drawn figures that contain the right
angle. Every square is of course similar to every other square, but not all similar
rectilinear figures are squares, for there is similarity in triangles and other polygonal
figures. Hence the argument establishing that the figure on the side subtending the right
angle, whether it be a square or any other kind of figure, is equal to similar and
similarly drawn figures on the sides about the right angle, proves something more general
and scientific then that which shows only that the square is equal to the squares. For
there the cause of the more general proposition that is proved becomes clear: it is the
rightness of the angle that makes the figure on the subtending side equal to the similar
and similarly drawn figures on the containing side, just as the obtuseness of the angle is
the cause of its being greater an the acuteness of the angle is the cause of its being
less.
How he proves the theorem in the sixth book will be evident there. But
now let us consider how he shows the theorem before us to be true, remarking only that he
does not prove the universal proposition here, since he has not yet explained similarity
in rectilinear figures, nor proved anything in general about proportion. Hence many of the
things here proved in a partial fashion are proved in that book more generally through the
use of the above method. In the present proposition the author of the Elements proves his
conclusion by means of the ordinary theory of parallelograms.
There are two sorts of right-angled triangles, isosceles and scalene.
In isosceles triangles you cannot find numbers that fit the sides; for there is no square
number that is de double of a square number, if you ignore approximations, such as the
square of seven which lacks one of being double the square of five. But in scalene
triangles it is possible to find such numbers, and it has been clearly shown that the
square on the side subtending the right angle may be equal to the squares on the sides
containing it. Such is the triangle in the republic, in which sides of three and four
contain the right angle and five subtends it, so that the square on five is equal to the
squares on those sides. For this is twenty-five, and of those the square of three is nine
and that of four sixteen. The statement, then, is clear for numbers.
[§] Certain
methods have been handed down for finding such triangles, one of them attributed to Plato,
the other to Pythagoras. The method of Pythagoras begins with odd numbers, positing a
given odd number as being the lesser of the two sides containing the angle, taking its
square, subtracting one from it, and positing the half of the remainder as the greater of
the sides about the right angle; then adding one to it this, it gets the remaining side,
the one subtending the angle. For example, it takes three, squares it, subtract one from
nine, takes the half of eight, namely, four, then adds one to this and gets five; and thus
is found the right-angled triangle with sides of three, four, and five. The Platonic
method proceeds from even numbers. It takes a given even number as one of the sides about
the right angle, divides it into two and squares the half, then by adding one to the
square gets the subtending side, and by subtracting one from the square gets the other
side about the right angle. For example, it takes four, halves it and squares the half,
namely two, getting four; then subtracting one it gets three and adding one gets five, and
thus it has constructed the same triangle that was reached by the other method. [§] For the square of this number is equal to the square of three and the
square of four taken together.
These remarks are somewhat outside our subject. But since the proof
given by the author of the Elements is clear, I do not think I should add anything
superfluous but should be content with what he has written, especially since those who
have made additions, such as the disciples of Heron and Pappus, have been obliged to
assume something proved in the sixth book, and for no material purpose.
[...]
Opmerking
Het gedeelte van de tekst hierboven tussen [§]
staat in vertaling van E.J. Dijksterhuis op de pagina over de
Stelling van Pythagoras.
[einde Opmerking]
2. Propositie VI-31
(Uitgebreide Stelling van Pythagoras) ![]()
Bedoelde propositie luidt (in vertaling van E.J. Dijksterhuis):
| Propositie VI-31 In rechthoekige driehoeken is een figuur, beschreven op de den rechten hoek onderspannende zijde, gelijk aan de op de den rechten hoek omvattende zijden op gelijke wijze beschreven gelijkvormige figuren. |
Opmerkingen
[1]
In het bovenstaande commentaar wordt Propositie VI-31 door Proclus
dus uitdrukkelijk als eigen vondst van Euclides aangemerkt.
[2]
Op de pagina "Boek VI" wordt het bewijs van VI-31
gegeven in een "moderne" notatie.
We laten hieronder het bewijs volgen zoals Euclides dat gegeven heeft
(naar een vertaling van C. Thaer: Die Elemente).
[einde Opmerkingen]
3. Bewijs van
Propositie VI-31 ![]()
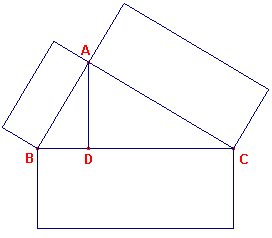 |
ABC zij een rechthoekige driehoek met rechte hoek BAC. Ik beweer, dat een
figuur op BC aan gelijkvormige [figuren], op BA, AC gelijkgetekende figuren, gelijk is. Men trekke de loodlijn AD. Daar men in de rechthoekige driehoek ABC uit de rechte hoek bij A op de basis BC de loodlijn AD getrokken heeft, zijn de driehoeken op de loodlijn, namelijk ABD, ADC gelijkvormig met zowel de gehele driehoek ABC als met elkaar. Daar ABC, ABD gelijkvormigzijn, is CB : BA = AB : BD. Daar hier de lijnstukken in verhouding tot elkaar staan, verhoudt zich de figuur op de eerste tot de op de tweede gelijkvormige en gelijkgetekende, als het eerste lijnstuk tot het derde [lijnstuk]. Zo verhoudt zich, als CB : BD, aldus de figuur op CB tot de op BA gelijkvormige en gelijkgetekende, en op dezelfde grond ook, als BC : CD, aldus de figuur op BC tot die op CA. Vervolgens verhoudt zich ook, als BC : (BD+DC), aldus de figuur op BC tot de gelijkvormige, op BA, AC gelijkgetekende samen. Nu is BC = BD + DC. Dus is ook de figuur op BC gelijkvormig met de gelijkgetekende figuren op BA, AC samen. ¨ |
Opmerking
Op de webpagina "Boek VI" staat ook een CabriJavapplet bij Prop. VI-31.
[einde Opmerking]