Incirkel - Ingeschreven cirkel van een driehoek

Overzicht  ][  Meetkunde | Uitcirkels

0. Overzicht terug

  1. Eigenschappen
  2. Punt en driehoek van Gergonne

Zie ook de pagina "Uitcirkels" voor enkele andere eigenschappen van de incirkel, in samenhang met de uitcirkels van een driehoek.
Zie ook de pagina "Om- en incirkel" (afstand tussen de middelpunten)

1. Eigenschappen terug

Stelling 1
- De punten op de bissectrice van een hoek hebben gelijke afstanden tot de benen van die hoek
- Een punt met gelijke afstand tot de benen van een hoek ligt op de bissectrice van die hoek.

Bewijs:

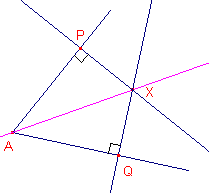incirkel1 Het bewijs van deze stelling kan worden geleverd via congruentie van de driehoeken XPA en XQA.
Voor het eerste deel van de stelling bewijzen we dat XP = XQ.
Voor het tweede deel bewijzen we dat de beide hoeken bij A aan elkaar gelijk zijn. ¨
Stelling 2
De bissectrices van een driehoek zijn concurrent.
Het gemeenschappelijk punt heet incentrum van de driehoek, meestal aangegeven met de letter I.

Bewijs:

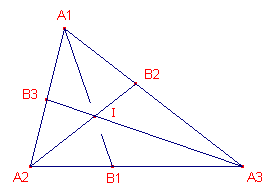incirkel2 Voor het snijpunt I van de bissectrices van A2 en A3 geldt:
d(I, A1A2) = d(I, A3A2)
d(I, A2A3) = d(I, A1A3),
waaruit dus volgt:
d(I, A2A1) = d(I, A3A1).
I ligt dus ook op de bissectrice van A1. ¨
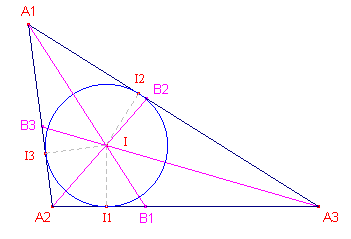incirkel3
Gevolg
Het gemeenschappelijk punt is middelpunt van een cirkel die aan de zijden van de driehoek raakt.
Deze cirkel heet incirkel (ook wel ingeschreven cirkel) van de driehoek.

De projecties van het punt I op de zijden van de driehoek bepalen de incirkel (ingeschreven cirkel) van de driehoek.
[einde Gevolg]
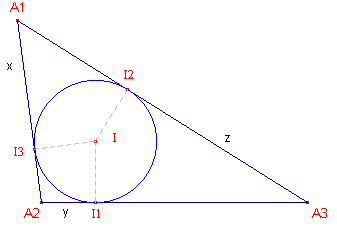incirkel3b Lengte van de raaklijnstukken

Zijn x, y, z de lengtes van de raaklijnstukken uit opvolgend A1, A2, A3.
Nu is x + y + z = "halve omtrek" = s, en y + z = a,
zodat
   x = s - a
En verder:
   y = s - b, z = s - c.

2. Punt en driehoek van Gergonne terug

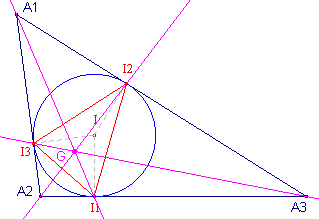incirkel4 Driehoek I1I 2I 3 heet de driehoek van Gergonne van driehoek A.
De lijnen AiIi snijden elkaar in het Gergonne-punt van driehoek A.

Zie verder de pagina's
- Transversalen, paragraaf 4.5
- Gergonne-punt en Gergonne-driehoek
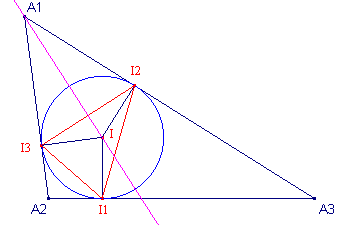incirkel5
Stelling 3
De lijnen AiI (bissectrices) zijn de middelloodlijnen van de zijden van de Gergonne-driehoek.

Bewijs:
A1I3 = A1I2 en I I3 = I I2.
Vierhoek A1I3I I2 is een vlieger. De diagonalen A1I en I2I3 staan dus loodrecht op elkaar, waarbij A1I door het midden gaat van I2I3. ¨

begin pagina
[incirkel.htm] laatste wijziging op: 26-06-02