Het raakprobleem van Apollonius (2)

Overzicht  ][  Raakprobleem (1) | Inversie | Geschiedenis | Meetkunde

Overzicht  terug

  1. Inleiding
  2. Basisconstructies

1. Inleiding terug
Hieronder staan enkele constructies die gebaseerd zijn op 'standaard' bewerkingen, zoals vermeningvuldiging en toepassing van machten.
Voor toepassingen met hoofdzakelijk inversie zie de pagina "Raakprobleem (1)".
Hieronder worden de volgende codes gebruikt:

       punten lijnen cirkels code
I. 1 1 1  zie A300
II. 2 1 0 S210  B
III. 2 0 1 S201  B
IV. 1 2 S120  B
V. 1 0 2 S102
VI. 1 1 1 S111

De gevallen VII tm. X. komen op deze pagina niet aan de orde.

In enkele gevallen komt ook een bijzondere ligging van de objecten ter sprake. Deze zijn hierboven aangegeven met B. Bij de constructies worden de bijzondere gevallen genoemd onder Opmerkingen.

2. Basisconstructies terug

II - S210 - Twee punten A en B en een lijn m terug

figuur
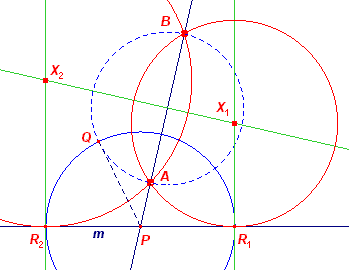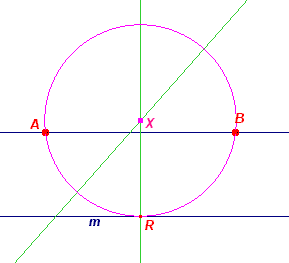
S210a		 apol210 Zie figuur S210a.
Zij P het snijpunt van AB met de lijn m.
Voor een raakpunt R geldt nu: PR2 = PA · PB.
We kunnen nu een willekeurige cirkel construeren die gaat door A en B. Het raaklijnstuk PQ (uit P aan die cirkel) is dan gelijk aan PR.
In de figuur hiernaast is daarvoor de cirkel met middellijn AB gekozen.
De cirkel met middelpunt (P, PQ) snijdt de lijn m in de punten R1 en R2. Dit zijn de raakpunten van de gezochte cirkels X1 en X2. De middelpunten daarvan liggen op de middelloodlijn van AB en op elk van de loodlijnen in R op m.

Er zijn maximaal 2 oplossingen.

Zie Opmerking [6] voor drie andere constructies.
figuur
S210b

apol210b

 Opmerkingen
[1] Er is geen oplossing als A en B aan verschillende kanten van m liggen.
[2] Indien een van de punten (A of B) op m ligt, is er slechts één oplossing.

[3] Zie figuur S210b.
Indien de beide punten gelijke afstand hebben tot m is bovenstaande constructie niet mogelijk, immers dan is de lijn AB evenwijdig met m.
In dit geval is het snijpunt R van de middelloodlijn van AB en de lijn m het raakpunt van de gezochte cirkel.
Hierdoor reduceert het probleem tot S300 (cirkel door drie punten: A, B, R).
figuur
S210c

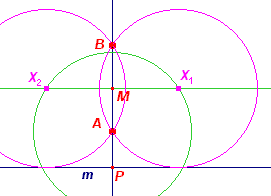
apol210c

 [4] Zie figuur S210c.
Is AB _|_ m, dan ligt het middelpunt X op de middelloodlijn van AB, welke lijn dan evenwijdig is met m.
De straal van de gezochte cirkel is dan de afstand MP tussen die middelloodlijn en de lijn m.
De cirkel (A, MP) - of (B, MP) - snijdt dan de middelloodlijn in de punten X1 en X2.

[5]
Klik hier voor de oplossing met inversie (A210).


[6]
Hieronder volgen nog drie alternatieve oplossingen van S210.
Deze alternatieven zijn aangedragen tijdens een discussie over het Apollonius' lijn-lijn-punt-probleem tussen 'beantwoorders van vragen' op WisFaq.

figuur
S210d		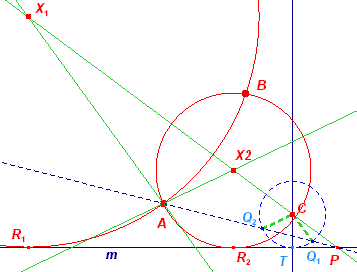 apol210j [6a] Zie figuur 210d.
(Met dank aan Johan -Andros- Deryckere)
 
De gezochte middelpunten, X1 en X2, moeten liggen op de middelloodlijn van AB. Deze lijn snijdt de lijn m in P.
Op de mddelloodlijn kiezen we een (willekeurig) punt C dat dient als middelpunt van een cirkel die in ieder geval al in T aan m raakt.
We willen nu deze cirkel vanuit P zo 'opblazen' - vermenigvuldigen, dat de productcirkel door A (en dan ook door B) gaat, en nog steeds rakend aan m.
Trek de lijn AP die cirkel C in de punten Q1 en Q2 snijdt.
Trek vervolgens de lijnen door A evenwijdig aan CQ1 en aan CQ2. Deze snijden de middelloodlijn van AB in de gezochte middelpunten X1 en X2.
figuur
S210e		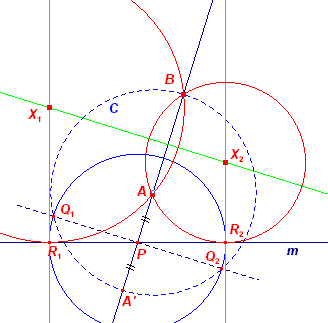 apol210f1 [6b] Zie figuur 210e
(Met dank aan Floor van Lamoen)
 
P is hier weer het snijpunt van AB en m.
A' is het beeld van A bij puntspiegeling in P. C is de cirkel op A'B. De lijn in P loodrecht op AB snijdt C in de punten Q1, Q2. Nu is
(Q1P)2 = Q1P · Q2P  =  PA' · PB = PA · PB
De punten R1, R2 op m, en daarmee ook de punten X1, X2 op de middelloodlijn van AB,  kunnen nu via de cirkel (P, PQ1) worden gevonden.
figuur
S210f		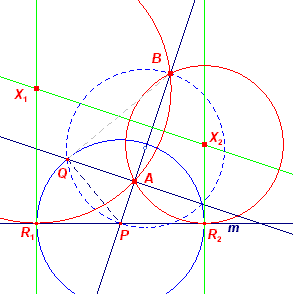 apol210f2 [6c] Zie figuur 210f
(Met dank aan Floor van Lamoen)
 
De cirkel op PB wordt door de loodlijn in A op AB (oa.) gesneden in het punt Q.
In driehoek PQB is Q een rechte hoek (Thales-cirkel), zodat geldt:
PQ2 = PA · PB
Met de cirkel (P, PQ) kunnen dan weer de punten R1, R2 op m worden gevonden.
Enzovoort.

[einde Opmerkingen]

III - S201 - Twee punten A en B en een cirkel K terug

figuur
201a		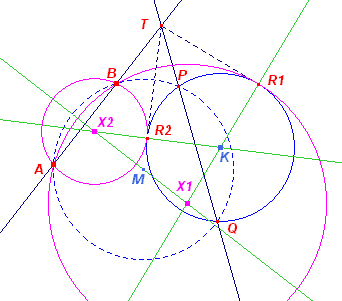 apol201 Het middelpunt X van de gezochte cirkel ligt op de middelloodlijn van het lijnstuk AB.
Kiezen we nu een punt M op die lijn en tekenen we met M als middelpunt een cirkel die de cirkel K in de punten P en Q snijdt (en door A en B gaat), dan geldt voor het snijpunt T van de lijnen AB en PQ dat
TB · TA = TP · TQ
De gezochte cirkel is dan die cirkel waarvoor TR2 = TP · TQ.
We kunnen het punt R dus construeren als raakpunt van een raaklijn uit T aan cirkel K.
Er zijn twee van deze lijnen: TR1 en TR2.
Het punt X ligt dus ook op KR1 of op KR2.
De snijpunten van deze lijnen met de middelloodlijn van AB levert de gezochte middelpunten X1 en X2.
figuur
201b		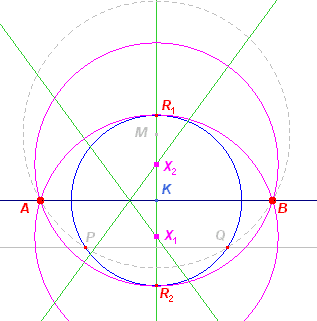 apol201b Opmerkingen
[1] Er zijn geen oplossingen als een van beide punten binnen de cirkel ligt. En evenmin als beide punten op de cirkel liggen.
[2] Er is één oplossing als beide punten op een raaklijn aan cirkel K liggen.

[3] (zie figuur 201b)
Er zijn twee congruente oplossingen als A en B symmetrisch tov. het punt K (dus op een middellijn van cirkel K) liggen. In dit geval is de lijn PQ evenwijdig met de lijn AB.
De middelloodlijn van AB bepaalt dan de beide raakpunten R1 en R2.
Het probleem reduceert zich hierdoor tot S300 (cirkel door A, B, R).

[4]
Klik hier voor de oplossing met inversie (A201)

[einde Opmerkingen]

IV - S120 - Een punt A en twee lijnen m en n terug

figuur
120a		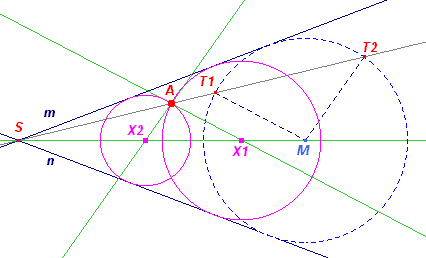 apol120 Zij S het snijpunt van beide lijnen.
Het gezochte middelpunt X ligt op de bissectrice van de hoek tussen m en n (waarbinnen het punt A ligt).
Kiezen we op deze bissectrice een punt M en tekenen we een cirkel met M als middelpunt die beide lijnen raakt, dan bepalen de snijpunten T1 en T2 van SA met deze cirkel twee met A overeenkomstige punten bij een vermenigvuldiging met S als centrum.

Opmerkingen
[1] Er zijn geen oplossingen als A samenvalt met S. Evenmin als de lijnen evenwijdig zijn en A "buiten die lijnen" ligt.
figuur
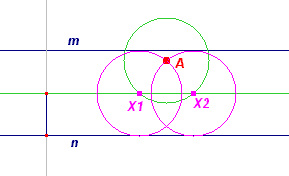120b		 apol120b [2] (zie figuur 120b)
Als m en n evenwijdig zijn, en A in het binnengebied ligt, dan ligt X op de middenparallel van de lijnen. Hierdoor is de straal eveneens bekend (de halve afstand van m en n).
Het punt X ligt dan ook op de cirkel met middelpunt A en straal gelijk aan die halve afstand.

[3]
Klik hier voor de oplossing met inversie (A120)

[einde Opmerkingen]

V - S102 - Een punt A en twee cirkels K1 en K2 terug

figuur
102a		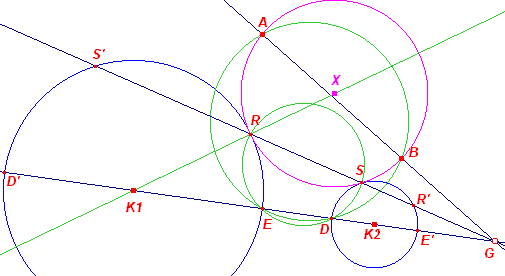 apol102a Analyse (bij uitwendige raking)
Zij cirkel X een van de gezochte cirkels, rakend in R en S aan de gegeven cirkels.
G is het uitwendig gelijkvormigheidspunt van de gegeven cirkels.
GA snijdt cirkel X voor de tweede keer in B.
De centraal snijdt de gegeven cirkels in D, D' en E, E'.
Uit de gelijkvormigheid volgt nu:
GS : GS' = GD : GD'.
Uit de machtseigenschappen van G volgt:
GR · GS' = GE · GD'.
Vermenigvuldiging van beide uitdrukkingen geeft dan:
GR · GS = GE · GD.
(Uit dit laatste volgt dat DERS een koordenvierhoek is.)

Maar er geldt ook:
GA · GB = GR · GS, zodat GA · GB = GE · GD.
Ook ABDE is dus een koordenvierhoek. Het punt B kan dus gevonden worden als snijpunt van de omcirkel van ADE met de lijn GA.
En hiermee is dit probleem teruggebracht tot het construeren van een cirkel door twee punten, te weten de punten A en B, en rakend aan een van beide gegeven cirkels K1 (of K2); geval S201.

Uiteraard geldt eea. ook voor inwendige raking. Daarbij wordt gebruik gemaakt van het inwendig gelijkvormigheidspunt van beide gegeven cirkels (zie figuur 102c).

figuur
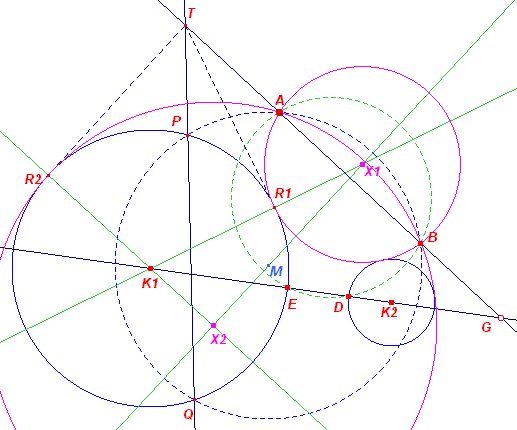
102b		 apol102b Constructie (bij uitwendige raking, gebaseerd op S201)
Via de omcirkel van ADE wordt het punt B op GA bepaald.
Daarna verloopt de constructtie geheel analoog aan die voor geval S201, betrekking hebbend op A, B, K1.

Zoals reeds opgemerkt, kunnen we nog twee cirkels vinden bij gebruikmaking van het inwendig gelijkvormigheidspunt van beide cirkels.

Er zijn dus maximaal vier oplossingen.
figuur
102c		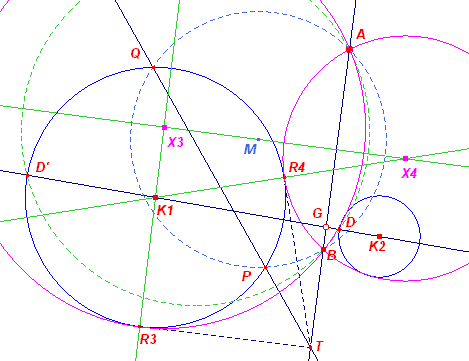 apol102c Constructie (bij inwendige raking, gebaseerd op S201)
Hierbij is het punt B geconstrueerd met behulp van de omcirkel van ADD'.
G is hier het inwendig gelijkvormigheidspunt.
Verder verloopt de constructie analoog aan die bij uitwendige raking.

Opmerkingen
[1]
Het aantal bijzondere gevallen hangt af van de ligging van beide cirkels ten opzichte van elkaar en ook van de ligging van het punt A daarbij.
We laten een beschrijving van die bijzondere gevallen hier achterwege.

[2]
Klik hier voor de oplossing met inversie (A102).

[einde Opmerkingen]

VI - S111 - Een punt A, een lijn m en een cirkel K terug

figuur
s111a		 apol111(ana) Analyse (bij uitwendige raking)
Stel X is het middelpunt van een gezochte cirkel.
Nu is DETR een koordenvierhoek (immers DRC = 90 en E = 90).
Zodat:
CD . CE = CR . CT
en ook (bij de gezochte cirkel):
CR . CT = CB . CA
Gevolg:
CD . CE = CB . CA
CB, ic. het punt B, kan dan worden geconstrueerd op CA (al vierde evenredige).
Of anders gezegd:
Ook DEAB is een koordenvierhoek, waarbij B het snijpunt is van CA met de omcirkel van die vierhoek.
Het constructieprobleem is daardoor teriggebracht tot het construeren van een cirkel door A en B die raakt aan de lijn m (zie geval S210).

Uiteraard geldt een en andere ook voor inwendige raking.

Er zijn dus op basis van geval S210 maximaal 4 oplossingen
figuur
s111b		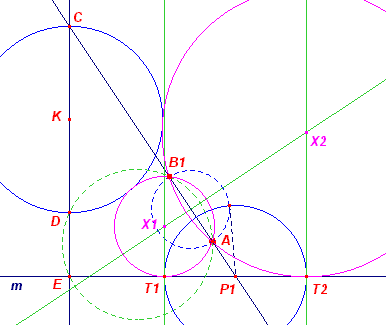 apol111b Constructie (bij uitwendige raking op basis van geval S210)

Teken de lijn CDE door K loodrecht op m.
Teken de omcirkel van DEA die CA snijdt in het punt B (in dit geval B1).
Bepaal de lengte van het raaklijnstuk uit P (in dite geval P1)aan de cirkel met middellijn AB.
De cirkel met middelpunt P ne zojuist bepaalde straal geeft dan de punten T1 en T2 (de raakpunten van de gezochtecirkels op m).
De punten X1 en X2 liggen dan op de middelloodlijn van AB en op de loodlijnen in T op m.
figuur
S111c		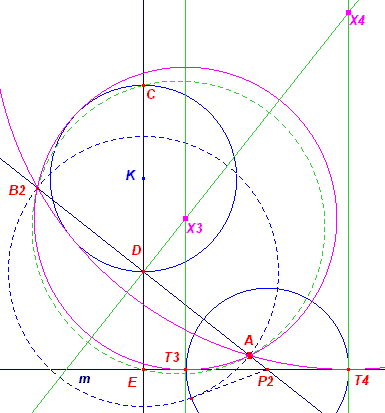 apol111c Constructie (bij inwendige raking op basis van geval S210)

We tekenen nu de lijn AD (in plaats van CA bij uitwendige raking).
Vervolgens wordt het punt B (in dit geval B2) bepaald met behulp van de omcirkel van CEA.
Voor het overige verloopt de constructie nu identiek aan die bij uitwendige raking.

Opmerkingen
[1]
Bijzondere gevallen kunnen zich natuurlijk ook hier voordoen.
Het punt A kent tov. de cirkel K drie liggingen (buiten K, op K en binnen K).
De lijn m kent eveneens drie liggingen (buiten K, rakend aan K, snijdend met K).
We zouden dus negen verschillende gevallen kunnen onderscheiden.
We laten een en ander hier achterwege.

[2]
Klik hier voor de oplossing met inversie (A111).

[einde Opmerkingen]

begin pagina
[raakprob(2).htm] laatste wijziging op: 13-09-03