Collineaties

Stelling 1 | Stelling 2 ][ Stelling van Feuerbach | Meetkunde

De collineatie van de vier punten H (hoogtepunt), Z (zwaartepunt), N (middelpunt negenpuntscirkel) en O (middelpunt omgeschreven cirkel) is geen uitzondering (zie de pagina "Feuerbach").

Op dezelfde manier als in bovenstaande stelling (zie de stelling over de Euler-lijn) kan bewezen worden.

Stelling 1
De drie lijnen door de middens van de zijden van een driehoek die evenwijdig zijn aan de bissectrice van de tegenover die zijden liggende hoek, zijn concurrent.
figuur 6a 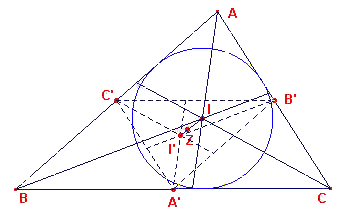figuur 6a Bewijs: (zie figuur 6a)
De punten A', B', C' zijn weer de middens van de zijden van driehoek ABC.
We kiezen nu een vermenigvuldiging met centrum Z (het zwaartepunt) en factor -½, Hierdoor gaat driehoek ABC over in driehoek A'B'C'.

Klik hier Animatie voor een animatie van deze stelling.

Maar ook de bissectricen van driehoek ABC worden daardoor vermenigvuldigd en deze hebben als beeld de bissectricen van driehoek A'B'C' die (zoals bekend) door één punt I' gaan, evenwijdig zijn aan de oorspronkelijke lijnen en ze gaan natuurlijk ook door de punten A', B' en C' (de middens van de zijden van driehoek ABC). ¨

We kunnen deze stelling gebruiken in de volgende stelling die eveneens gaat over het door één punt gaan van een drietal lijnen in een driehoek.

Stelling 2
De lijnen die de hoekpunten van een driehoek verbinden met de raakpunten van de aangeschreven cirkels op de tegenover de hoekpunten gelegen zijde, gaan door één punt J.
De punten J, Z (zwaartepunt) en I (middelpunt ingeschreven cirkel) zijn collineair, waarbij
JZ : ZI = 2 : 1.

Bewijs: (zie figuur 6b) Zijn A', B', C' de middens van de zijden van driehoek ABC, zijn K, K1, K2 de raakpunten van de aangeschreven cirkels aan de zijde BC en P, Q, R de raakpunten op de zijden van de ingeschreven cirkel.
We bewijzen allereerst dat AK // IA'.
We spreken een notatie af voor lengtes van enkele lijnstukken, ed.:

Nu is ah = 2pr  (= 2s). Dus h : r = 2p : a.
Of AS : IP = 2p : a.
We zullen nu aantonen dat deze verhouding gelijk is aan de verhouding KS : A'P. Volgens de cosinusregel is b2 = a2 + c2 - 2aBS, zodat BP = (a2 + c2 - b2) / (2a).

figuur 6b 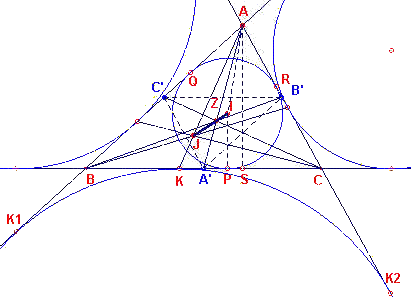figuur 6b Klik hier Animatie voor een animatie van deze stelling.

Aan de andere kant hebben we
BK = BK1 = AK1 - AB = p - c = (a + b - c)/2, omdat
AK  = ½(AK1 + AK2) = 
= ½(AB + BK1 + AC + CK2) 
= ½(AB + BK + AC + CK) 
= ½(a + b + c) = p.
Op basis hiervan vinden we nu
KS = BS - BK = (a2 + c2 - b2)/(2a)-(a + b - c)/2
= (a2 + c2 - b2 - a2 - ab + ac)/(2a)
= (c - b)(c + b + a)/(2a)
= p(c - b)/a

Verder is
BP = ½(BP + BQ)  = ½(BC - BP + BA - AQ)
= ½(BC + BA - CR - AR)  = ½(a + c - b)
= p - b
en dus
A'P = BP - BA' = p - b - a/2 = (c - b)/2
We krijgen dus de volgende verhouding
KS :  A'P = p(c - b)/a :  (c - b)/2 = (2p)/a = AS : ZP

Omdat de driehoeken ASK en IPA' gelijkstandig zijn, zijn de lijnen AK en IA' dus evenwijdig.

figuur 6c 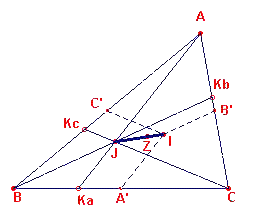figuur 6c De lijnen IA', IB', IC' zijn de beelden van de bissectricen van driehoek ABC bij een vermenigvuldiging met factor -½ ten opzichte van het punt Z (ze zijn dus de bissectricen van driehoek A'B'C; zie figuur 6c en ook de stelling over de Euler-lijn).

We kiezen nu een vermenigvuldiging met centrum Z en factor -2. Bij deze vermenigvuldiging gaat het punt I over in het punt J. De lijnen IA', IB', IC' gaan over in lijnen door J die daaraan evenwijdig zijn.

Verder is dan onmiddellijk duidelijk, dat
ZJ : ZI = 2 : 1. ¨

Verwijzing
Op het Cabri-werkblad "Over Spieker en Nagel" wordt aan bovengenoemde collineaties eveneens aandacht besteed.

¤ Terug naar de pagina "Over de cirkel van Feuerbach ..."

begin pagina
[feuerbach2.htm] laatste wijziging op: 23-04-03