Cabri werkblad - Spieker en Nagel

Cabri werkblad

Overzicht ][ Alle werkbladen | Meetkunde | Cabri

Overzicht - Over Spieker en Nagel

Zomaar een constructie?
Opdracht 1
Omtrekdeellijnen
Opdracht 2
Drie omtrekdeellijnen
Opdracht 3
Opdracht 4
S is een bijzonder punt, het middelpunt van de Spieker-cirkel
     Opdracht 5
     Opdracht 6
     Opdracht 7
Eigenschappen van het punt van Nagel
     Opdracht 8
     5.1. De eerste eigenschap
                 Opdracht 9
                 Opdracht 10
     5.2. De tweede eigenschap
                 Opdracht 11
                 Opdracht 12
     5.3. Te bewijzen: PB = s - c
     5.4. Stap voor stap naar het bewijs
                 Opdracht 13
Conclusie
Naschrift
Download

1. Zomaar een constructie?

figuur 1

Opdracht 1

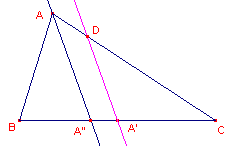Teken een (ongelijkbenige) driehoek ABC.

Construeer de deellijn van hoek A waarvan het snijpunt met BC het punt A" is.

Construeer ook het midden A' van BC.

Construeer de lijn door A' evenwijdig met reeds getekende deellijn.
Deze lijn snijdt één van de zijden met eindpunt A in het punt D.

Zomaar een vraag:
Is het punt D een bijzonder punt van de driehoek?

Vermoedelijk heb je op deze vraag geantwoord met "nee" of met "ik weet het (nog) niet".
Maar een bijzonder punt is het zeker wel.
Voordat we daarop ingaan maken we eerst een (niet-officiële) notatieafspraak.

figuur 2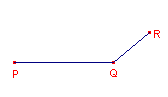

Afspraak
Met [PQR] bedoelen we de lengte van het gebroken lijnstuk van P via Q naar R; dus
[PQR] = |PQ| + |QR|.

We laten de beide absoluut strepen bij de lengtes van lijnstukken in hetgeen volgt weg tenzij er misverstand kan ontstaan over wat bedoeld is.

2. Omtrekdeellijnen

Nu dan verder met de bijzondere positie van het punt D bij driehoek ABC.
Voor het punt D (zie figuur 1) blijkt nu te gelden: CD = [DAB]

Je kan dit met Cabri nagaan door de lengtes van CD, DA en AB te meten.

Nu geldt dus ook (het volgt eenvoudig uit bovenstaande bewering over het punt D):
[A'CD] = [A'BAD]

Licht kort toe waarom dit dan inderdaad waar is.

De punten A' en D (daar ging het om) zijn dus zo op de omtrek gelegen, dat ze de omtrek halveren.
We noemen A'D daarom een omtrekdeellijn van driehoek ABC.
Natuurlijk is het zaak de eigenschap van het punt D te bewijzen. Zie daarvoor Opdracht 2.

Opdracht 2

figuur 3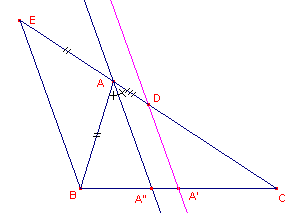

Bewijs dat A'D een omtrekdeellijn van driehoek ABC is.
Aanwijzing
Verleng CA met een lijnstuk AE waarbij AE = AB (zie figuur 3).
Kijk dan eens naar de ligging van het punt D op het lijnstuk CE.
Wat kan je in dit verband bewijzen omtrent A'D en BE?

3. Drie omtrekdeellijnen

Opdracht 3

figuur 4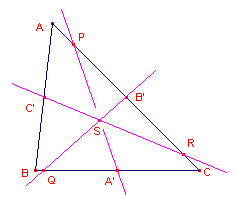

Teken de drie omtrekdeellijnen A'P, B'Q en C'R van driehoek ABC (een macro is misschien wel handig).

Wat valt je op?

Inderdaad, er geldt

Stelling
De omtrekdeellijnen van een driehoek gaan door één punt.

We zullen deze stelling bewijzen in:

Opdracht 4

figuur 5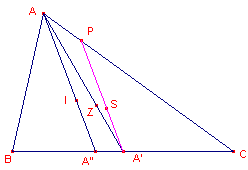

Kijk eens naar de hierboven staande figuur (figuur 5).
Hierin is I het snijpunt van de bissectricen van de driehoek (het middelpunt van de incirkel).
Z is het zwaartepunt van driehoek ABC.
Het punt S is ook al getekend, maar we gaan voorlopig alleen uit van I en Z.
We kiezen Z als centrum van een vermenigvuldiging d met factor -½.

Welk punt is het beeld van A onder de afbeelding d?
We schrijven d (A) = … .
Wat weet je nu van het beeld van de lijn AA" bij deze vermenigvuldiging? Noem twee eigenschappen.
Waarom valt d (AA") samen met de lijn A'P?

Het gemeenschappelijk punt I van de bissectricen van driehoek ABC ligt (natuurlijk) op AA".

Wat weet je nu van het beeld d

(I) van I?

Waarom gaan (dus) de omtrekdeellijnen door één punt?

Waarom is d

(I) = S?
4. S is een bijzonder punt, het middelpunt van de Spieker-cirkel

We kiezen opnieuw (zoals hierboven in Opdracht 4) de vermenigvuldiging d met centrum Z en factor -½.
We construeren nu het beeld van driehoek ABC.
Opdracht 5

figuur 6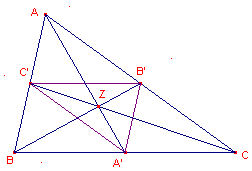

figuur 7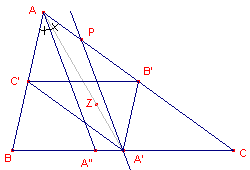

Zie figuur 6.

Vul in:
   d(A) = …
   d(B) = …
   d(C) = …
   d(ABC) = …
Wat weet je nu van de zijden van driehoek A'B'C' in vergelijking met die van driehoek ABC? Noem twee (of meer) eigenschappen.

Driehoek A'B'C' (zie nu figuur 7) noemen we de centrumdriehoek (ook wel zwaartepuntsdriehoek) van driehoek ABC.

Welke betekenis hebben de omtrekdeellijnen van driehoek ABC voor de centrumdriehoek A'B'C'?
Aanwijzing
Kijk naar parallellogram AC'A'B' en de hoeken daarvan. Gebruik ook de wetenschap, dat AA"//PA'.

We hebben nu (dus):

Stelling
Het punt S, het snijpunt van de omtrekdeellijnen van driehoek ABC, is het middelpunt van de ingeschreven cirkel van de centrumdiehoek van driehoek ABC
of, anders geformuleerd:
Een deellijn van de centrumdriehoek van driehoek ABC is omtrekdeelliijn van driehoek ABC.

figuur 8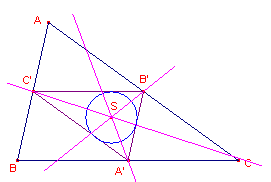

figuur 9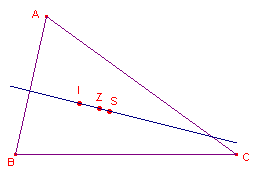

De ingeschreven cirkel (zie figuur 8) van de centrumdriehoek heet wel de Spieker-cirkel van driehoek ABC (genoemd naar de Duitse 19e eeuwse wiskundige Theodor Spieker).

Ook geldt nu (zie figuur 9):

Stelling
De punten I (middelpunt van de incirkel), Z (zwaartepunt) en S (middelpunt van de Spieker-cirkel) van een driehoek liggen op één lijn, waarbij IZ : ZS = 2 : 1.

Bewijs deze stelling
Aanwijzing
Zie paragraaf 3.

De genoemde lijn heet ook wel de lijn van Nagel van driehoek ABC.
Deze reden daarvoor is gelegen in het feit, dat er nog een vierde bijzonder punt op deze lijn ligt, namelijk het punt van Nagel (genoemd naar de Duitse wiskundige Christian Heinrich von Nagel, 1803-1882).
In Opdracht 7 zullen we het "punt van Nagel" van een driehoek construeren.

Eerst nog even een kleine opdracht tussendoor.

Opdracht 6

figuur 10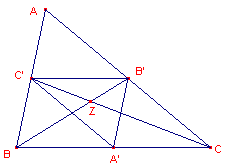

Laat zien (bewijs), dat het zwaartepunt van de centrumdriehoek van een driehoek samenvalt met het zwaartepunt van de driehoek zelf.
Aanwijzing
Gebruik middenparallellen!

Het feit dat beide driehoek hetzelfde zwaartepunt hebben, kunnen we verderop in dit werkblad gebruiken.

Opdracht 7 - constructie van het punt van Nagel

figuur 11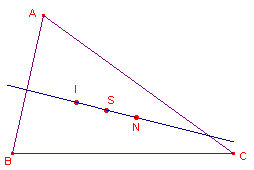

We gaan uit van de punten I en S van driehoek ABC (zie figuur 11).

Construeer nu het punt N =

Puntspiegeling(I, S).
Gevolg

S ligt midden tussen I en N.

Hiermee is het punt van Nagel geconstrueerd.

Met welke vermenigvuldiging kunnen we het punt van Nagel van een driehoek construeren als we uitgaan van het punt I en het punt Z?

5. Eigenschappen van het punt van Nagel

Het punt van Nagel heeft ook enkele andere eigenschappen.
De eerste (hier te vermelden) eigenschap is snel af te leiden door gebruik te maken van de vermenigvuldiging d_N met centrum N en factor ½.
Opdracht 8

Driehoek A₁B₁C₁ is het beeld van driehoek ABC onder de afbeelding d_N.

figuur 12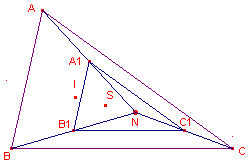

Vul in:
d_N(I) = …
d_N(ingeschreven cirkel van ABC) = …

Formuleer nu een eigenschap van de ingeschreven cirkels van de centrumdriehoek van ABC en van die van A₁B₁C₁.

Als r de straal is van de incirkel van ABC, druk dan de straal van de Spieker-cirkel en en die van de incirkel van driehoek A₁B₁C₁ uit in r.

Kan je hieruit concluderen dat de centrumdriehoek en driehoek A₁B₁C₁ dezelfde incirkel hebben?
Verklaar je antwoord.

5. 1. De eerste eigenschap

We keren nu de zaak min of meer om en bewijzen

Stelling
Het middelpunt (I) van de incirkel van een driehoek (ABC) is het punt van Nagel van de centrumdriehoek van die driehoek (ABC).

Opdracht 9

figuur 13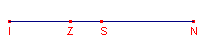

Bekijk de ligging van de punten I, Z, S en N van driehoek ABC (zie figuur 13).

Bewijs dat IZ : ZN = 1 : 2.
Kies nu de vermenigvuldiging d_Z met centrum Z en factor - ½ (deze afbeelding gebruikten we ook in paragraaf 3).
Er geldt dus d_Z(I) = S.

Nb.
Het maakt dus niet uit (zie Opdracht 6) of we Z als zwaartepunt van driehoek ABC of van de centrumdriehoek nemen; ze vallen immers samen.

Opdracht 10

Laat de inhoud van Opdracht 9 nu goed tot je doordringen.
Kijk dan naar de volgende algemene procedure:

Ga uit van het middelpunt (noem het P, maar vervang deze naam door een passende in een specifieke situatie) van de incirkel van een driehoek.
Voer met het zwaartepunt van de driehoek als centrum (noem het hier maar Q) een vermenigvuldiging uit met factor - ½.
Noem het beeld van Q in dit geval R.
Welk punt van de driehoek is het punt R?

Geef een redenering, gebaseerd op bovenstaande algemene procedure, waarmee je de laatst genoemde stelling hierboven kan bewijzen.
Aanwijzing
Zie de Opdracht 6 en Opdracht 7.

5.2. De tweede eigenschap

Deze eigenschap zullen we formuleren na de volgende opdracht.
Opdracht 11

figuur 14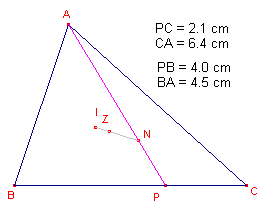

Kies een nieuw Cabri werkblad en teken daarop driehoek ABC.

Construeer van driehoek ABC de punten I (middelpunt incirkel), Z (het zwaartepunt) en N (het punt van Nagel).
De lijn AN snijdt de zijde BC in het punt P.

Zo maar een vraag:
Is het punt P een bijzonder punt van driehoek ABC?

Gebruik Cabri om de lengtes van de volgende gebroken lijnstukken te berekenen (zie figuur 14).

Bereken:
[PCA] = PC + CA = …
[PBA] = PB + BA = …
Formuleer een vermoeden omtrent de punten A en P.

Er geldt (inderdaad):

Stelling
Een lijn door het hoekpunt van een driehoek en het punt van Nagel van die driehoek is een omtrekdeellijn van die driehoek.

Ook deze stelling zullen we via enkele opdrachten bewijzen. Wel moeten we daarbij enig rekenwerk in (aan) driehoek ABC verrichten.

Opdracht 12

figuur 15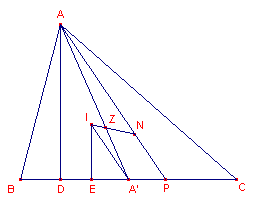

Ga uit van een driehoek waarin de punten I, Z en N zijn geconstrueerd. Zie figuur 15.
Gebruik weer de vermenigvuldiging d_Z met centrum Z en factor -½.

Vul in:
   d_Z(N) = …
   d_Z(A) = …
   d_Z(NA) = …
Waarom is nu IA' // NA?

Teken ook de loodlijnen op BC door het punt A (lijnstuk AD) en door het punt I (lijnstuk IE).

Waarom zijn de driehoeken ADP en IEA' gelijkvormig?

Afspraak

De omtrek a+b+c van een driehoek stellen we gelijk aan 2s.
Dus 2s = a + b+ c.
Ons doel vanaf nu
: het berekenen van de lengte van het lijnstuk BP (zie figuur 15).
Als P inderdaad een omtrekdeellijn is, dan moet gelden:
[PBA] = s = PB + BA = PB + c.
5.3. Te bewijzen: PB = s - c

We kunnen dit bewijzen door wat rekenwerk in driehoek ABC te verrichten.
We bewijzen allereerst in een hulpstelling iets over de raaklijnstukken aan de ingeschreven cirkel van een driehoek.

figuur 16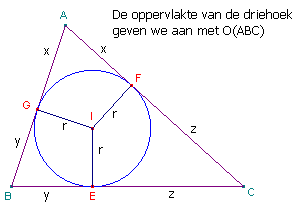

Hulpstelling
Zie figuur 16 voor het gebruik van de verschillende lengtes.
In driehoek ABC geldt:
[1] O(ABC) = rs
[2] x = s - a, y = s - b, z = s - c

Bewijs:
[1]
O(IBC) = ½ ra, O(ICA) = ½ rb, O(IAB) = ½ rc.
Optelling geeft
O(ABC) = ½ ra + ½ rb + ½ rc = ½ r (a + b + c) = ½ r . 2s = rs.
[2]
Voor de omtrek (*) geldt: x + y + z = s
en verder ook y + z = a
Dus, na substitutie, hebben we x = s - b. Op dezelfde manier vinden we de uitdrukkingen voor y en z.

(*) Nb.
Bewijs eventueel zelf (nog eens) dat de raaklijnstukken (zoals het lijnstuk x uit A) vanuit aan punt aan een cirkel aan elkaar gelijk zijn.

5.4. Stap voor stap naar het bewijs

De rest van het bewijs van de stelling uit paragraaf 5.2 delen we op in enkele stappen (zie bij elke stap figuur 15).

Opdracht 13
[Stap 1]
Bewijs met behulp van de cosinusregel, toegepast in driehoek ABC, dat

.
Aanwijzing. Kijk naar driehoek ABD voor cos(B).

[Stap 2]
Bewijs, met gebruikmaking van de hulpstelling, dat EA' = ½ a - (s - b).

[Stap 3]
AD is hoogtelijn van driehoek ABC. We kunnen dus AD eveneens gebruiken om O(ABC) uit te rekenen.
Bewijs, met gebruikmaking van de hulpstelling, dat .

[Stap 4]
Uit de gelijkvormigheid van de driehoeken ADP en IEA' (zie Opdracht 12) volgt:
DP : EA' = AD : IE = AD : r.
Leid hieruit af, dat .

[Stap 5]
Bewijs nu, uitgaande van BP = BD + DP, dat BP = s - c.

6. Conclusie

Iets anders geformuleerd dan hierboven (in paragraaf 5.2) hebben we dus bewezen:

Stelling
Het Nagel-punt van een driehoek is het snijpunt van de omtrekdeellijnen die door de hoekpunten gaan.

Er is niets tegen om het punt S, het snijpunt van de omtrekdeellijnen die door de middens van de zijden gaan, het Spieker-punt te noemen.
We hebben dus al eerder bewezen (in paragraaf 3):

Stelling
Het Spieker-punt van een driehoek is het snijpunt van de omtrekdeellijnen die door de middens van de zijden gaan.

In figuur 17 zien we alle laatst behandelde punten en lijnen nog eens bij elkaar.

figuur 17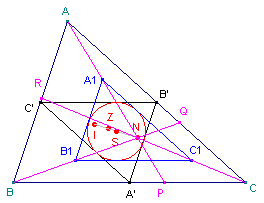

7. Naschrift

Ook over de punten P, Q en R (als eindpunten van de omtrekdeellijnen door de hoekpunten) is nog wel wat op te merken.
We vermelden hier (zonder bewijs weliswaar):

Stelling (zie fguur 18)
De punten P, Q en R zijn de raakpunten van de uitcirkels (uitwendig aan de zijden rakende cirkels) aan de zijden van de driehoek
of anders geformuleerd
De lijnen door de raakpunten van de uitcirkels op de zijden van een driehoek en gaande door de tegenoverliggende hoekpunten zijn concurrent in het punt van Nagel van de driehoek.

figuur 18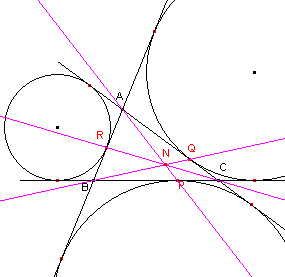

Opmerkingen
[1]
Deze eigenschap wordt bewezen op de pagina "Transversalen" als toepassing van de Stelling van Ceva.

[2]
Klik hier voor een behandeling van het verband tussen het punt van Nagel en de Fuhrmann-cirkel.
Klik hier voor een behandeling van het punt van Spieker in samenhang met de aancirkels van een driehoek.

Klik hier voor de samenhang tussen de incirkel van een driehoek en de Negenpuntscirkel.

8. Download
De Cabri-figuren die op deze pagina zijn gebruikt, kunnen in één bestand via deze webpagina worden gedownload.
In dat bestand zijn ook enkele Cabri-macro's en enkele andere figuren opgenomen.
Klik hier om het downloaden te starten [ZIP-bestand, 23Kb].

Deze pagina is (in iets gewijzigde vorm) ook beschikbaar in PDF-formaat.
spina.pdf [ca. 92 Kb]

[spina.htm] laatste wijziging op: 20-03-2005