Het punt van Spieker

Inleiding  |  Spieker-punt   |  Tenslotte  ][  Spieker en Nagel  |  Meetkunde

1. Inleiding
Het Spieker-punt (punt van Spieker) van een driehoek is het middelpunt van de ingeschreven cirkel (incirkel) van de centrumdriehoek van die driehoek.
Zie in figuur 1 het punt S.

figuur 1 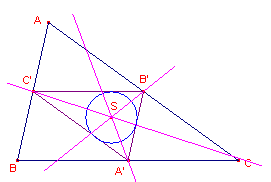spina8 Voor andere eigenschappen van het Spieker-punt dan in de paragraaf  2 genoemde, zie het Cabri-werkblad "Spieker en Nagel".

2. Een bijzondere eigenschap van het Spieker-punt
Op het genoemde Cabri-werkblad (pagina "Spieker en Nagel") wordt in het Naschrift de volgende stelling vermeld:

figuur 2 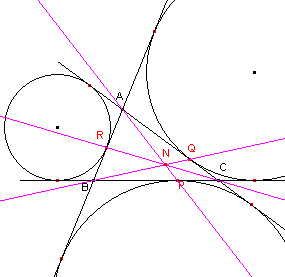spina18
Stelling
De lijnen door de raakpunten van de uitcirkels op de zijden van een driehoek en gaande door de tegenoverliggende hoekpunten zijn concurrent in het punt van Nagel van de driehoek.

Er is blijkbaar een verband tussen de uitcirkel en het punt van Nagel (zie weer het Cabri-werkblad "Spieker en Nagel", Opdracht 7).
Het punt van Nagel wordt daarbij uitgaande van het Spieker-punt geconstrueerd.

Hieronder wordt een direct verband gelegd tussen het Spieker-punt van een driehoek en de uitcirkels van die driehoek. Er geldt namelijk:

Stelling
Het Spieker-punt van een driehoek is het machtpunt van de uitcirkels van die driehoek.

Voor de definitie van het machtpunt van drie cirkels zie de pagina "Macht van een punt", stelling 6.

Bewijs: zie figuur 3, waarin het Spieker-punt van driehoek ABC is aangegeven met I'.

figuur 3 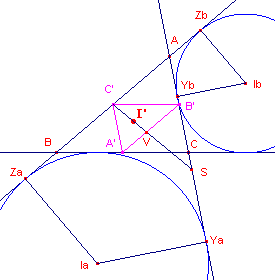spieker1 In de figuur hiernaast is A'B'C' de centrumdriehoek van ABC.
Ia en Ib zijn resp. de middelpunten van de uitcirkel aan de zijde a en van de uitcirkel aan de zijde b.
Ya, Za, Yb, Zb zijn de raakpunten op de betreffende zijden.
De lijn C'I' snijdt A'B' in V en AC in S.
We zullen eerst aantonen, dat C' het midden is van ZaZb, en dat S het midden is van YaYb.

Nb.
ZaZb en YaYb zijn gemeenschappelijke raaklijnen aan de beide cirkels!

AZb is raaklijnstuk aan de uitcirkel aan de zijde b. Dus: AZb = s - c.
BZa is raaklijnstuk aan de uitcirkel aan de zijde a. Dus BZa = s-c.
C' is dus het midden van ZaZb.
Vanwege de evenwijdigheid van de zijden A'C' en B'S zijn de driehoeken SB'V en C'A'V gelijkvormig. Daaruit volgt dan:
SB' : C'A' = B'V : A'V = (wegens het feit, dat C'V een bissectrice is in driehoek A'B'C')
                 = C'B' : C'A' = BC : CA = a : b
Of ook
SB' : ½b = a : b, zodat SB' = ½a.
SC = SB' - B'C = ½a - ½b.
Nu is verder CYb = s - a (raaklijnstuk uit C aan de uitcirkel aan b) en CYa = s - b (raaklijnstuk aan de uitcirkel aan a).
Daaruit volgt dan weer:
SYb = s - a + ½a - ½b = s - ½a - ½b, en
SYa = s - b - (½a - ½b) = s - ½a - ½b.
Zodat SYa = SYb.
S is dus het midden van YaYb.
De lijnstukken ZaZb en YaYb zijn gemeenschappelijke raaklijnstukken aan de beide uitcirkels.
Uit C en S kunnen dus gelijke raaklijnstukken getrokken worden aan die cirkels.
Met andere woorden: C en S liggen op de machtlijn van beide uitcirkels (zie de pagina "Macht van een punt").
En: I' ligt op de machtlijn van de uitcirkels aan a en b.

Evenzo kunnen we bewijzen, dat I' op de machtlijn ligt van de uitcirkels aan de zijden a en c.
I' is dus het machtpunt van de drie uitcirkels. ¨

3. Tenslotte
Met het Spieker-punt als middelpunt kunnen we de zogenoemde machtcirkel van de drie uitcirkels tekenen. Deze cirkel staat loodrecht op de drie uitcirkels.
Dan blijkt, dat de zijden van de centrumdriehoek bijzondere snijpunten hebben met deze machtcirkel (zie figuur 4).

figuur 4 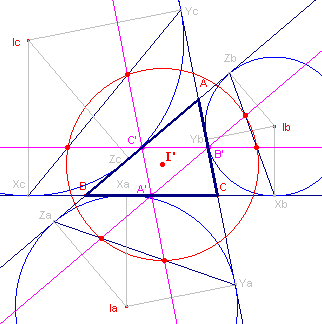spieker2 De zijden van de centrumdriehoek snijden de machtcirkel van de drie uitcirkels in punten die op XcYc, YaZa en ZbXb liggen.

Van deze eigenschap geven we hier geen bewijs.

begin pagina

[spieker.htm] laatste wijziging op: 29-07-02