Driehoeksconstructie: a, b - c, hc

a, b - c, h_c
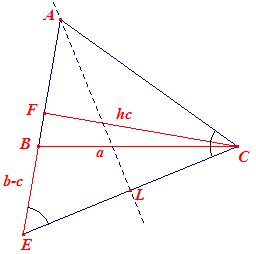	Uitgaande van een reeds geconstrueerde driehoek ABC (met b > c): dan: -- kies op het verlengde van AB een punt E zo, dat AE = b; dan is BE = b - c; -- driehoek BCE is dan construeerbaar met CF = hc als hoogtelijn uit c en met zijden BC = a en BE = b - c (zie constructie); -- driehoek AEC is gelijkbening.
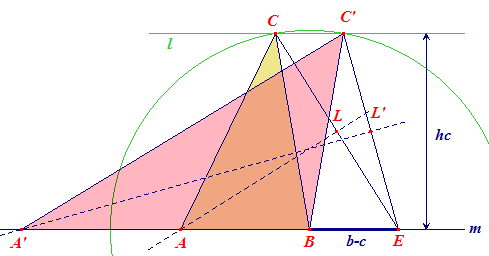	Constructiebeschrijving -- teken een lijn m en kies daarop de punten B en E, met BE = b - c; -- het punt C ligt op een afstand h_c van BE: de lijn l op afstand h_c van BE is dus een meetkundige plaatst van C; -- C ligt ook op de cirkel (B, a); -- snijpunt van beide geeft dan het punt C; -- het punt A ligt op de middeloodlijn van CE; -- snijding van die lijn met de lijn BE geeft dan het punt A. Uit de constructie blijkt dat er maximaal twee oplossingen zijn.

[p : ab-chc.htm] laatste wijziging op: 20-05-2005