Driehoeksconstructies: a, A, hb + hc en a, A, hb - hc

Constructies ][ Driehoeksconstructies | Meetkunde | Cabri

Overzicht constructies

a, A, h_b+h_c

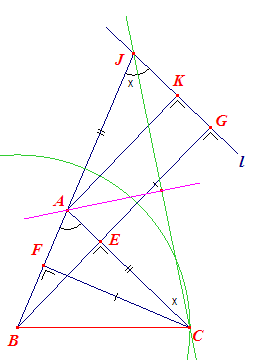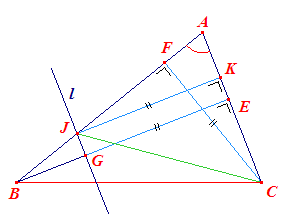
We gaan uit van een gegeven driehoek ABC.
BE en CF zijn de (gegeven) hoogtelijnen van die driehoek.
Verleng nu BE (= h_b) met EG = CF = h_c. l is de lijn door F evenwijdig met AC. l snijdt het verlengde van BA in J.
De driehoeken BAE en AJK zijn dan gelijkvormig (hh), zodat BJG = BAC = A.
Driehoek BJG kan dus worden geconstrueerd (ZHH).
K is de projectie van A op l. AKGE is dan een rechthoek, zpdat AK = EG = h_c.
De rechthoekige driehoeken AFC en JKA zijn dan congruent (ZHH), zodat
AJ = CA = b en dus BJ = BA + AJ = c + b = b + c.
Uitgaande van [ a, A, h_b+h_c ] hebben we nu dus ook [ A, a, b + c ] en dit is construeerbaar.

De constructie is echter ook direct uitvoerbaar, uitgaande van het punt B en driehoek BJG (zie de figuur hiernaast).
We hebben namelijk:
BAC = AJK = A en BAC = AJC + ACJ (buitenhoek van ACJ)
zodat:
AJC = ACJ = ½A, immers AJ = CA
JC is dan de bissectrice van hoek J, en deze lijn is dan een meetkundige plaats van het punt C.

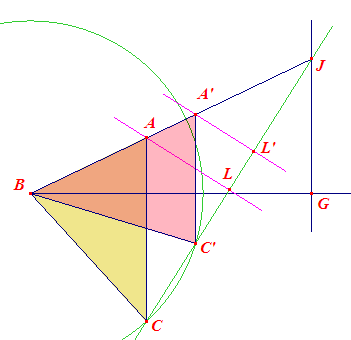Ook de cirkel (B, a) is een meetkundige plaats van C, waardoor het punt C construeerbaar is.
Het punt A vinden we dan als snijpunt van AJ en de middelloodlijn van CJ.

Uit de constructie blijkt dat er twee oplossingen zijn (zie de figuur hiernaast), immers de bissectrice van J snijdt de cirkel (B, a) in hoogstens twee punten:
-- ABC en A'BC' (via de middens L en L' van opvolgend JC en JC').

Opmerking
In driehoek BJG hebben we de elementen:
b + c, h_b + h_c, A
Twee van deze elementen bepalen telkens het derde, immers van BJG is reeds bekend, dat hoek G = 90°.
Ook [ a, b + c, h_b + h_c ] is dus construeerbaar!

a, A, h_b - h_c

aAhb-hc

We gaan uit van een gegeven driehoek ABC, waarin C > B (immers uit het gegeven volgt dat h_b > h_c).
Kies op BE ( = h_b) het punt G zo, dat EG = CF = h_c.
Dus: BG = h_b - h_c.
De lijn l door G is evenwijdig met AC en snijdt AB in J. K is de projectie van J op AC.
Nu is: CF = GE = JK, zodat de driehoeken AFC en AKJ congruent zijn (ZHH).
Daaruit volgt dat AC = AJ = b.
Dan is BJ = BA - AJ = c - b
We zien dus dat [ a, A, h_b - h_c ] gelijkwaardig is met [ A, a, c - b ]; en deze laatste is constueerbaar.

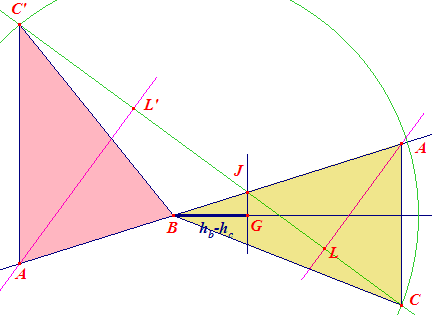Ook hier kan de constructie direct worden uitgevoerd, uitgaande van het punt B en driehoek BJG, waarin hoek J gelijk is aan A..
Verder is driehoek ACJ gelijkbenig en dan is AJC = ½(180 - A) = 90 - ½A.
JC is dus bissectrice van hoek GJA. Die bissectrice is dus een meetkundige plaats van het punt C.
C ligt ook op de cirkel (B, a), zodat we C kunnen vinden als snijpunt van beide.
A vinden we dan als snijpunt van het verlengde van BJ en de middelloodlijn van JC.

Ook nu vinden we twee oplossingen: ABC en A'BC', bepaald via de middens L en L' van opvolgend CJ en C'J.

Opmerking
In driehoek BJG vinden we de elementen:
A, h_b - h_c en c - b.
'Twee van deze elementen bepalen telkens het derde, immers van BJG is reeds bekend, dat hoek G = 90°.
Ook [ a, c - b, h_b - h_c ] is dus construeerbaar!

[p : aAhb+hc.htm] laatste wijziging op: 20-04-2005