Driehoeksconstructie: a, B, b - ha

Theorie | Constructie ][ Driehoeksconstructies | Meetkunde | Cabri

Theorie

a, B, b-h_a
	We gebruiken bij de constructie de definitie van parabool: de meetkundige plaats van de punten die gelijke afstand hebben tot een punt en een lijn. Daarnaast wordt gebruik gemaakt van de Euclidische constructie van het snijpunt van een rechte lijn met een (virtuele) parabool. Zie voor deze constructie de pagina "Parabool: meetkundige eigenschappen".

Constructie

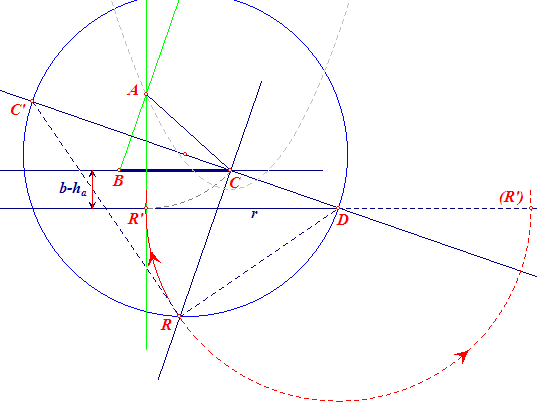Constructiebeschrijving
(Met dank aan Anneke Grünefeld-Raaphorst.)

Uit het gegeven b - h_a, blijkt dat b > h_a.
Teken het lijnstuk BC (gegeven) en de halve lijn BA (immers hoek B is gegeven).
Teken ook de lijn r evenwijdig met BC en op afstand b-h_a van BC aan de kant van BC waar A niet ligt.
Nu geldt voor het punt A dat AC = b en d(A, r) = b, zodat A ligt op de parabool met C als brandpunt en r als richtlijn.
We moeten nu het snijpunt (de snijpunten) van BA met deze parabool construren (met passer en liniaal).
Deze constructie verloopt (conform de beschrijving op de pagina "Parabool: meetkundige eigenschappen") via de cirkel met middellijn C'D (C' is de gespiegelde van C in BA; D is het snijpunt van r met CC'). Op basis hiervan is dan in driehoek DRC':
DR² = DC · DC'
Het punt R' op r met DR' = DR bepaalt dan via de loodlijn in R' op r het gezochte punt A.
Waarna ook het lijnstuk AC getekend kan worden.

Opmerking
Er zijn twee punten A die voldoen.
Op de lijn r is nog een tweede punt R' (R' tussen haakjes) te vinden, waarvoor geldt: (DR^' )² = DC · DC'.

[p : aBb-ha2.htm] laatste wijziging op: 07-01-2006