Parabool: meetkundige eigenschappen en constructies

Overzicht  ][  Kegelsneden | Anal. meetkunde | Cabri ]

Overzicht terug

[ Pagina 1 ] [ Pagina 2 ] [ Pagina 3 ] [ Pagina 4 ]

  1. Definitie en gevolgen daarvan
         (oa. Hoofdeigenschap van de raaklijn)
  2. Snijpunten van een lijn en een parabool
  3. Subtangens en subnormaal
         3.1. Subtangens cabrisignal
         3.2. (Sub)normaal     cabrisignal
  4. Andere constructies
         4.1. Twee raaklijnen en de richtlijn
         4.2. Drie andere gegevens
         4.3. Oneigenlijke punten
  5. e.v. Zie pagina 2

1. Definitie en gevolgen daarvan terug

Definitie
Een parabool is de meetkundige plaats van de punten X waarvoor geldt d(X, F) = d(X, r), waarbij F een vast punt is (het brandpunt) en r een vaste lijn (de richtlijn van de parabool).
Zie ook "Kegelsneden en hun vergelijkingen" (en eventueel "Analytische meetkunde").

Uit de definitie volgen onmiddellijk twee constructies.

Constructie 1
parab0 Voor een punt P van de parabool hebben we:
- P ligt op de loodlijn in het punt Pr op de richtlijn;
- P ligt op de middelloodlijn van FPr.
P is dus het snijpunt van die lijnen. ¨

Gevolg
We kunnen op deze manier een willekeurig aantal punten van de parabool construeren.
[einde Gevolg]

Opmerking
Het punt A, het mdden van het lijnstuk tussen F en de projectie R van F op r heet de top van de parabool.
[einde Opmerking]
Constructie 2
parab0-1 De afstand, bedoeld in de definitie, geven we aan met a.
Dan geldt voor een punt P van de parabool:
- P ligt op de cirkel met middelpunt F en straal a
- P ligt op de lijn // met r en op afstand a van r
De parabool is dus (ook) de meetkundige plaats van de snijpunten van de cirkel en de lijn. ¨

Gevolg
Ook met deze constructie kunnen we een willekeurig aantal punten (in tweetallen) van de parabool construeren.
[einde Gevolg]
terug
Stelling 1 - Hoofdeigenschap van de raaklijn
De raaklijn in een punt P van een parabool (F, r) maakt gelijke hoeken met de brandpuntvoerstraal en de as-richting.
Nb. De brandpuntvoerstraal van het punt P is de lijn PF.

Bewijs:

parab0-a Uit Constructie 1 volgt onmiddellijk, dat FPQ = PrPQ.
We moeten nu alleen nog aantonen, dat PQ (de middelloodlijn van FPr) raaklijn is aan de parabool.

Stel P' is een tweede snijpunt (dus verschillend van P) van PQ met de parabool.
Dan geldt:
- P' op de parabool: P'P'r = PF
- P' op de middelloodlijn: P'Pr = P'F
Nu is driehoek PrP'P'r een gelijkbenig driehoek met een hoek van 90º (bij P'r, als basishoek).
Dat is niet mogelijk. Dus de lijn PQ heeft geen tweede snijpunt met de parabool.
PQ is dus raaklijn. ¨

Opmerking - Zie ook de pagina "De lijn van Steiner".

2. Snijpunten van een lijn en een parabool terug
De parabool wordt gedefinieerd via de in ligging gegeven F en r. We noteren dat in hetgeen volgt als parabool(F, r).

Constructie 3
parab0-b Zij p de lijn.
We zoeken dus op p gelegen middelpunten van cirkels die gaan door F en raken aan de richtlijn r.
Omdat p dan een middellijn van zo'n cirkel is, gaat die cirkel ook door het p-spiegelbeeld F' van F.
We moeten dus de middelpunten van cirkels construeren die door twee punten gaan (F en F') en raken aan r.
Dit is een van de gevallen van het Raakprobleem van Apollonius (210).
De lijn FF' snijdt de lijn r in G.
Nu is GH2 = GF · GF'
De punt P1', P2' met GP1' = GP2' = GH zijn de projecties van de middelpunten op r.
De snijpunten van de loodlijnen in P1' en P2' op r met de lijn p zijn dan de gevraagde snijpunten. ¨

Gevolg
Uit de ligging van F' en F kunnen we afleiden hoeveel oplossingen er zijn.
1.
F en F' liggen aan verschillende kanten van r. Door F en F' is dan geen cirkel mogelijk die raakt aan r. Geen oplossingen.
2.
F' ligt op de richtlijn r. De punten P1' en P2' vallen dan samen met F'. Maar dan vallen ook P1 en P2 samen. In dit geval is de lijn p raaklijn aan de parabool.
Hieruit volgt dan onmiddellijk:

Stelling 2
Een lijn p raakt aan een parabool als het p-spiegelbeeld van het brandpunt F op de richtlijn r ligt.

Gevolgen van Stelling 2
1.
De raaklijn is middelloodlijn van FF' (zie Stelling 1)
2.
Het beeld van de richtlijn in een raaklijn gaat door het brandpunt F.
[einde Gevolgen]

Op basis van Stelling 2 kunnen we de volgende constructie uitvoeren.

Constructie 4
parab0-b2 Gegeven: parabool (F, R), lijn m
Te construeren: een raaklijn aan de parabool die evenwijdig is met m.
Constructie:
- Construeer het snijpunt F' van de loodlijn uit F op m met de richtlijn.
- Construeer de middelloodlijn van FF'.
- Deze middelloodlijn is de raaklijn // m. ¨

Zie ook Pagina 2, paragraaf 6

3. Subtangens en (sub)normaal terug
     3.1. Subtangens / 3.2 Subnormaal

3.1. Subtangens terug

parab0-c2 In de figuur hiernaast:
- P' is de projectie van P op de as;
- Q is het snijpunt van de raaklijn p met de as.
P'Q heet de subtangens van P bij de parabool. ¨
Stelling 3
De top A van een parabool (F, R) is het midden van de subtangens van een punt P van de parabool.

Klik hier >Animatie< voor een Cabrijavapplet bij Stelling 3.

Bewijs:

parab0-c Pr is het p-spiegelbeeld van F, zodat FS = SPr.
De driehoeken FSQ en PrSP zijn congruent (ZHH, HZH), zodat ook PS = SQ.
We bekijken nu de lijn s door S // r.
Wegens s // r geldt: S door het midden A van RF (in driehoek PrRF). s is dan de topraaklijn.
In PQP' is s // PP' en S is het midden van PQ. zodat A ook het midden is van P'Q. ¨

Gevolg
We kunnen hiervan gebruik maken voor de constructie van de raaklijn in een gegeven punt P van een parabool (F, r).
Zie Constructie 5.
[einde Gevolg]
Constructie 5
parab0-d - Construeer de as door F loodrecht op r. Deze snijdt de rcihtlijn r in R.
- Construeer P' als project van P op de as.
- Construeer A als midden van FR.
- Q is het A-spiegebeeld van P'.
- PQ is de raaklijn in P. ¨
Stelling 4a
De topraaklijn is de meetkundige plaats van de voetpunten der loodlijnen op de raaklijn in de punten van de parabool.

Bewijs:

parab0-e parab0-f FSP = 90º.
Zie verder Stelling 3. ¨
Gevolg
De cirkel met de brandpuntvoerstraal als middellijn raakt aan de topraaklijn.

We kunnen Stelling 4a ook anders formuleren

Stelling 4b
Een been van een rechte hoek waarvan het hoekpunt op een rechte lijn ligt, omhult een parabool als het andere been door een vast punt gaat.

Klik hier >Animatie< voor een Cabrijavapplet bij Stelling 4b.

Gevolg
Bij gegeven P op de parabool (F, r) kan de raaklijn geconstrueerd worden als de verbindingslijn van P met het snijpunt van de loodlijn uit het midden van PF op de topraaklijn.
[einde Gevolg]

3.2. (Sub)normaal terug

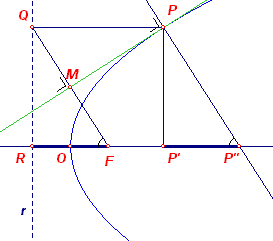parab1 In de figuur hiernaast:
- P' is de projecte van P op de as;
- P" is het snijpunt van de lijn door P loodrecht op de raaklijn.
De lijn PP" heet normaal van P.
Het lijnstuk P'P" heet de subnormaal van P.
Stelling 5
De subnormalen van de punten van een parabool hebben een constante lengte (gelijk aan de parameter van de parabool).

Klik hier voor het bewijs van Stelling 5  cabrisignal.

Op Stelling 5 kunnen we eveneens een constructie van de raaklijn in een punt P van de parabool (F, r) baseren.

Constructie 6
parab0-f2 - Construeer de as door F loodrecht op de richtlijn. De as snijdt de richtlijn in R
- Construeer de projectie P' van P op de as.
- Bepaal het beeld P" van P' bij een translatie over de vector RF.
Het lijnstuk FR heet de parameter van de parabool.
- De raaklijn is de lijn die in P loodrecht staat op de lijn PP". ¨

4. Andere constructies terug
Hierboven zijn constructies gegeven bij gegeven brandpunt F en richtlijn r. Hieronder gegeven we enkele constructies indien andere gegevens van de parabool bekend zijn.

4.1. Twee raaklijnen en de richtlijn terug

Constructie 7
parab11 Gegeven: richtlijn r en raaklijnen p1 en p2 aan de parabool
Te construeren: het brandpunt F
Constructie:
- Construeer de spiegelbeelden r1 en r2 van de richtlijn in beide raaklijnen.
Volgens het Gevolg van Stelling 2 gaan deze spiegebeelden door F.
- Construeer het snijpunt van r1 en r2. Dit is dan het brandpunt F.

Merk op dat de snijpunten S1 en S2 van de raaklijnen met de richtlijn bij de spiegeling invariant zijn.
¨

4.2. Drie andere gegevens terug

parab12 Zoals bij Constructie 7 reeds is opgemerkt: het snijpunt van de raaklijn en de richtlijn is bij spiegeling van de richtlijn in de raaklijn invariant.
Daarvan kunnen we bij enkele andere constructies gebruik maken.
Immers, Vierhoek PPrSF is dan een rechthoekige vlieger.
Constructie 8     Constructie 9 Constructie 10
parabc8 parabc9    parabc10
Twee raaklijnen gegeven, en het brandpunt.
Construeer de richtlijn.
Constructie: F1 en F2 zijn de spiegelbeelden van F in de raaklijnen t1 en t2.
F1F2 is dan de richtlijn r.		 De richtlijn, een raaklijn en een punt P gegeven.
Construeer het brandpunt.
Constructie: r1 is het spiegelbeeld van r in t1.F ligt op r1. F ligt ook op de cirkel (P, PPr)
Er zijn twee oplossingen.		 De as, de top A en een punt P gegeven.
Construeer het brandpunt en de richtlijn.
Constructie: Q is het spiegelbeeld van P' in A.
QP is dan de raaklijn in P. De topraaklijn snijdt de raaklijn in het midden S van PQ.
F ligt op de loodlijn in S op PQ; enz.

4.3. Oneigenlijke punten terug
Bij enkele constructies kunnen (moeten) we gebruik maken van het feit, dat de parabool raakt aan de oneigenlijke rechte in het oneigenlijk punt van de paraboolas.
Klik hier voor een tweetal van dergelijke constructies.
In een van de constructies wordt Constructie 10 gebruikt bij het construeren van brandpunt en richtlijn, als de as-richting en drie punten van de parabool gegeven zijn.

[ Pagina 1 ] [ Pagina 2 ] [ Pagina 3 ] [ Pagina 4 ]

begin pagina
[parab.htm] laatste wijziging op: 24-11-03