Parabool: meetkundige eigenschappen en constructies (5)

Overzicht  ][ Kegelsneden | Anal. meetkunde | Cabri

Overzicht terug

[ Terug naar Pagina 1 ] [ Pagina 2 ] [ Pagina 3 ] [ Pagina 4 ]

     Gebruik van oneigenlijke punten
          4.3.1. Drie punten en de asrichting
          4.3.2. Vier raaklijnen

Gebruik van oneigenlijke punten terug

4.3.1. Drie punten en de asrichting terug
Van de parabool met vergelijking y = ax2 + bx + c weten we dat de symmetrie-as evenwijdig is met de y-as.
Als we drie punten van de parabool kennen, dan kunnen we de vergelijking van de parabool bepalen (a, b, c berekenen).

Of ook:
We moeten de volgende constructie kunnen uitvoeren.

Constructie 21
Gegeven: drie punten van de parabool (F, r) en de asrichting
Te construeren: F, r

Opmerking
In onderstaande figuren zijn de parabool en de richtlijn r wel weergegeven. Daarvan wordt bij de constructies geen gebruik gemaakt.
In de figuren is een horizontale lijn getekend, met daarop punten als (4), (5), ... Deze lijn geeft de oneigenlijke rechte weer. Punten tussen ( en ) zijn oneigenlijke punten.
[einde Opmerking]

Constructie:

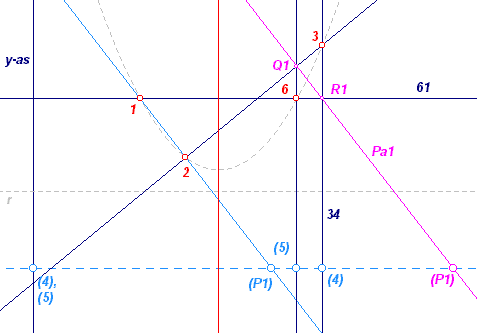
parab51

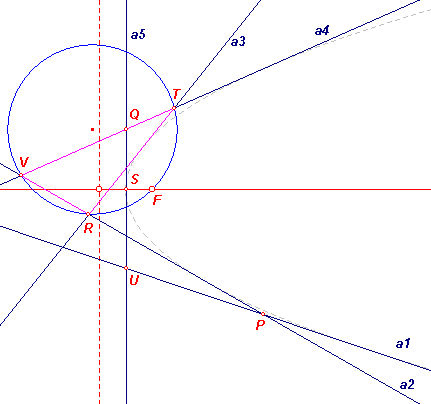
 Zijn 1, 2, 3 de gegeven (eindige) punten.
De oneigenlijke rechte raakt in de (samenvallende) punten 4, 5 aan de parabool.
Dit punt (4, 5) is tevens het oneigenlijke punt van de as (dus ook van de lijn die de asrichting, d.i. de y-as, bepaalt).
Zij 6 het spiegelbeeld van 1 in de (nog onbkende) parabool-as.
We bekijken nu de zeshoek 123456 en passen daarop de stelling van Pascal toe.
Zij 12 /\ 45 = P1, 23 /\ 56 = Q1, 34 /\ 61 = R1
Volgens de Stelling van Pascal (in dit geval voor kegelsneden) zijn dan de punten P1, R1, Q1 (in deze volgorde te construeren) collineair (zie de lijn Pa1).
We kunnen met deze wetenschap het punt 6 vinden.
De as is dan de middelloodlijn van het lijnstuk 16.
.

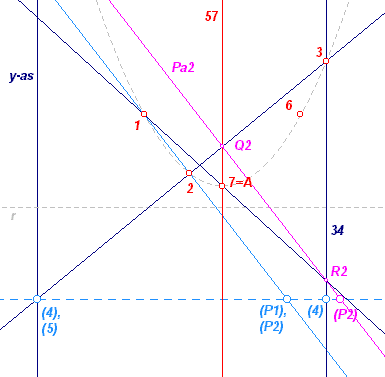
 parab52

 Vervolgens.
Zij 7 het tweede snijpunt van de as met de parabool. Het andere snijpunt is het raakpunt (4 = 5) op de oneigenlijke rechte.
Het punt 7 is dus de top van de parabool.
Bekijk de zeshoek 123457.
Zijn dan P2 = P1, Q2 = 23 /\ 57, R2 = 34 /\ 71. Deze punten zijn volgens de Stelling van Pascal weer collineair (zie de lijn Pa2).
Volgorde van constructie: P1, Q1, R1.
Het punt 7 = A is dan te vinden.
.
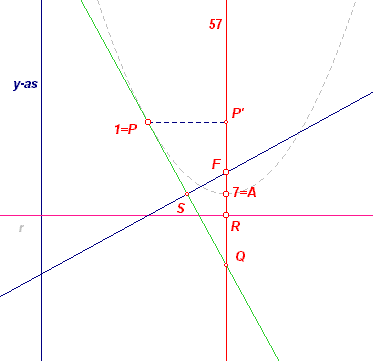parab53 [De volgende constructie is gebaseerd op Constructie 10 van Pagina 1].

Zij nu P = 1 en P' de projectie van P op de as.
Het punt A is het midden van de subtangens van P.
Zij Q het A-spiegelbeeld van P'. Dan is QP de raaklijn in P aan de parabool.
S zij het midden van QP. Het brandpunt F ligt dan op de loodlijn in S op PQ.
Het snijpunt van deze loodlijn en de as is dan het punt F.
Het A-spiegelbeeld R van F is dan het snijpunt van de as met de richtlijn, waarmee ook r gevonden is.
¨

4.3.2. Vier raaklijnen terug

Constructie 22
Gegeven: vier raaklijnen aan een parabool (F, r)
Te construeren: F en r

Opmerkingen
[1]
Een andere eenvoudiger constructie dan hieronder staat, vinden we als Constructie 13 op "Pagina 2".
In onderstaande constructie - die niet eenvoudig is - wordt echter gebruik gemaakt van de oneigenlijke rechte.
[2]
In enkele figuren hieronder is een (lichtblauwe) verticale lijn getekend, met daarop punten als (Q1), (U1), ... Deze lijn geeft de oneigenlijke rechte weer. Punten tussen ( en ) zijn oneigenlijke punten.
In de figuren zijn de parabool en de richtlijn r wel in (lichtgrijs) weergegeven. Daarvan wordt bij de constructies geen gebruik gemaakt.
[einde Opmerkingen]

Constructie:

parab54

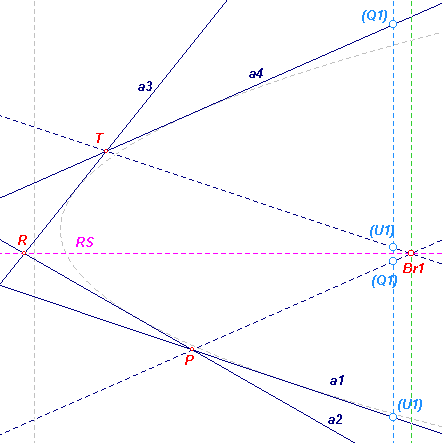
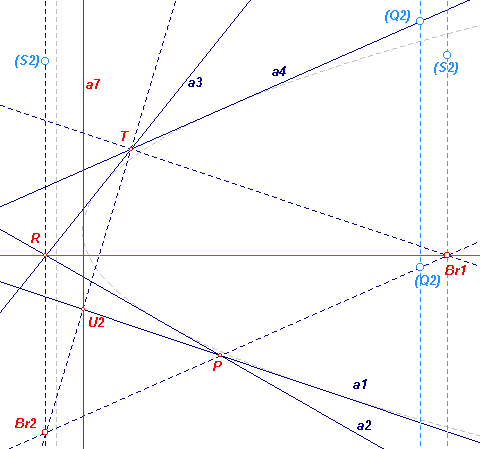
 Zijn a1, a2, a3, a4 de gegeven raaklijnen. Bekijk nue de door die raaklijnen ingesloten zeszijde a1a2a3a4a5a6, waarbij a5 = a6 de raaklijn is in het oneigenlijke punt van de parabool-as.
Zij nu
a1 /\ a2 = P, a4 /\ a5 = Q1,
a2 /\ a3 = R, a5 /\ a6 = S1,
a3 /\ a4 = T, a6 /\ a1 = U1.
Het punt S is dan het oneigenlijk punt van de parabool-as. De lijn RS geeft dus de asrichting.
De lijnen PQ, RS, TU zijn concurrent in het punt Br1 (punt van Brianchon; zie Stelling van Brianchon voor cirkels).
Met behulp van het bovenstaande is de asrichting (RS, door Br1) te construeren.
.
parab55 We hebben dan op basis van de asrichting ook de richting van de topraaklijn.
De topraaklijn, a7, is raaklijn uit een punt S2 van de oneigenlijke rechte.
We bekijken daarom de door de raaklijnen ingesloten zeszijde a1a2a3a4a5a7.
Hierbij hebben we:
a1 /\ a2 = P, a4 /\ a5 = Q2,
a2 /\ a3 = R, a5 /\ a7 = S2,
a3 /\ a4 = T, a7 /\ a1 = U2.
Het punt S2 is een oneigenlijk punt. Het bepaalt de richting van de topraaklijn.
Ook nu zijn PQ, RS, TUS concurrent in een Brianchon-punt, Br2.
Op deze manier is de topraaklijn a7 te construeren.
.

parab56

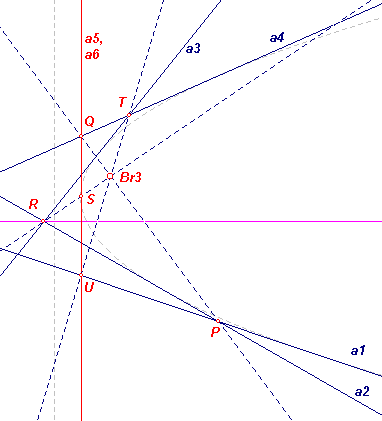
 Van de parabool zijn nu vijf raaklijnen bekend: a1, a2, a3, a4, a7 (in de figuur is de lijn a7 aangegeven met a5,a6).
Hiermee construeren we het raakpunt S (de top van de parabool) op de topraaklijn a7.
We beschouwen de door die raaklijnen omschreven zeszijde a1a2a3a4a7a7.
Hierbij is:
a1 /\ a2 = P, a4 /\ a7 = Q,
a2/\ a3 = R, a7 /\ a7 = S,
a3 /\ a4 = T, a7 /\ a1 = U
PQ, RS, TU zijn concurrent in het punt Br3.
Nu is het punt S te construeren als het snijpunt van a7 met RBr3.
.

parab57

 De as van de parabool gaat nu door S en staat loodrecht op de topraaklijn.
Voor de constructie van het brandpunt F op die as gebruiken we Stelling 8 van Pagina 2:
De omcirkel van de driehoek die gevormd wordt door drie raaklijnen aan een parabool, gaat door het brandpunt van die parabool.
We kiezen de raaklijnen a4, a3, a2 - dus in bovenstaande tekening driehoek TVR, met
V = a4 /\ a2.
Het punt F is een van de snijpunten van de omcirkel van TVR en de as.
De richtlijn r kan op de gebruikelijke manier via F en S worden gevonden.
¨

[ Terug naar Pagina 1 ] [ Pagina 2 ] [ Pagina 3 ] [ Pagina 4 ]

begin pagina
[parab5.htm] laatste wijziging op: 27-11-03