Parabool: meetkundige eigenschappen en constructies (4)
Overzicht ][ Kegelsneden | Anal. meetkunde | Geschiedenis | Cabri
[ Pagina 1 ] [ Pagina 2 ] [ Pagina 3 ] [ Pagina 4 ]
14. Oppervlakte van
een paraboolsegment ![]()
N.B. We gebruiken in hetgeen volgt F als oppervlaktefunctie.
| Lemma 1 F(segment ASB) = 2/3 F(AA'B'B) , waarbij AA'B'B het omgeschreven parallellogram is van segment ASB. |
| Bewijs: | |
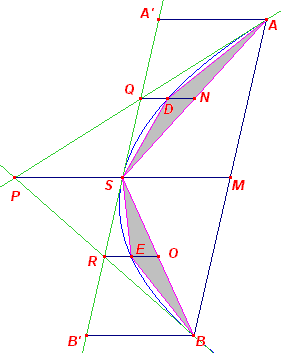 |
In de figuur hiernaast: - PA en PB zijn raaklijnen, AB is raakkoorde - PM (evenwijdig met de as) snijdt de parabool in S en de koorde AB in het midden M - S is het midden van PM (Pagina 3, Stelling 11a) - AA'B'B is het omgeschreven paralellogram van het segement ASB - A'B' (de raaklijn in S) snijdt de raaklijnen opvolgend in Q en R - QN en RO zijn middellijnen van de parabool, dus ook: - D is het midden van QN, N is het midden van AS (Pagina 3, Stelling 11a), en - E is het midden van RO, O is het midden van BS F(ASD) = ½F(ASQ) = ¼F(ASP) = ¼F(ASM)
= 1/8F(ASB) |
| (*) Dit resultaat komt als Propositie 1 voor in Archimedes' bewijs voor de kwadratuur van de parabool (zie Paragraaf 15). |
|
We kunnen nu Stelling 1 bewijzen:
Bewijs van Stelling 1
Uit F(ASB) = ½F(APB) volgt dat
F(segment ASB) = 2/3F(AA'B'B) = 2/3F(APB),
zodat inderdaad de verhouding der delen gelijk is aan 1 : 2. ¨
| Stelling 2 De oppervlakte van een raaklijnendriehoek van een parabool is de helft van de oppervlakte van de driehoek waarvan de raakpunten de hoekpunten zijn. |
| Bewijs: | |
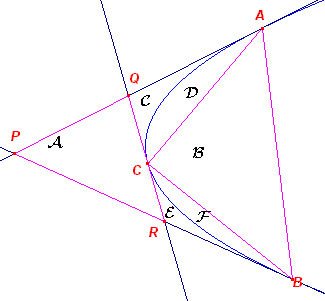 |
In nevenstaande figuur zijn 6 vlakdelen aangegeven met de letters
A,B,C,D,E,F. Deze letters stellen de oppervlakte van die vlakdelen voor. Volgens Stelling 1 is: A + C + E = ½(B + D + F) En ook: C = ½D E = ½F, zodat A = ½B Hetgeen bewezen moest worden. ¨ |
15.
Archimedes' kwadratuur van de parabool ![]()
Lemma 1 (zie het bewijs in Paragraaf 14) is ook door Archimedes
(Archimedes van Syracuse, 287-212vC, Sicilië)
bewezen. Hij deed dat deels in 'Methodenleer der Mechanische Leerstellingen' en bijna
volledig in 'Over de kwadratuur van de parabool'.
We geven hieronder Archimedes' bewijs uit de 'Methodenleer' (geparafraseerd) weer.
Aan Eratosthenes
In 1906 werd in een klooster te Konstantinopel een Grieks handschrift gevonden uit de
10e eeuw n.C. Dit handschrift bevatte onder andere Archimedes' Methodenleer der
mechanische Leerstellingen, aan Eratosthenes (Eratosthenes van Cyrene, 276-194vC, Cyrene, Noord-Afrika).
Archimedes schrijft daarin aan Eratosthenes onder meer:
"Daar ik echter, zooals ik reeds vroeger zeide, dat Gij
een flink geleerde zijt, en niet slechts een bewonderaar [van mathematisch onderzoek], zoo
heb ik voor goed bevonden U uiteen te zetten en in dit zelfde boek neer te leggen een
eigenaardige methode, waardoor U de mogelijkheid geboden zal worden een aanwijzing te
vinden om enkele mathematische kwesties door de Mechanica te onderzoeken. En dit is naar
mijn overtuiging ook even zoo nuttig om de stellingen zelve te bewijzen; want veel wat mij
het eerst door de Mechanica duidelijk geworden is, werd daarna bewezen door de Geometrie,
omdat behandeling door die andere methode nog niet door bewijs gefundeerd was; het is nl
gemakkelijker, als men door deze methode aanvankelijk een voorstelling van de vragen
gekregen heeft, het bewijs te verzinnen dan dit zonder een voorloopige voorstelling te
ontdekken. Zoo zal men ook aan de bekende leerstellingen, wier bewijzen Eudoxos het
eerst gevonden heeft, nl. van den kegel en de pyramide, dat zij 1/3
zijn, de kegel van den cylinder en de pyramide van het prisma, die hetzelfde grondvlak en
dezelfde hoogte hebben, Demokritos een niet gering aandeel toekennen, die het eerst van
het genoemde lichaam de uitspraak gedaan heeft zonder bewijs. We verkeeren echter in de
omstandigheid ook de nu te publiceren stelling [op dezelfde wijze] vroeger gevonden te
hebben, en voelen ons nu gedrongen de methode bekend te maken, deels omdat wij vroeger
daarover gesproken hebben, opdat niemand geloove dat wij ijdel gepraat verbreid hebben,
deels in de overtuiging daardoor geen gering nut voor de Mathesis te stichten; ik neem nl.
aan, dat deze of gene van de tegenwoordige of toekomstige vorschers door de hier
verklaarde methode ook andere stellingen zal vinden, die ons nog niet zijn ingevallen.
Eerst verklaren wij nu, wat ons ook het eerst duidelijk geworden is door de Mechanica, dat
een segment van een parabool 4/3 is
van den driehoek, die dezelfde grondlijn en dezelfde hoogte heeft, dan echter
achtereenvolgens de afzonderlijke, door de genoemde methode gevonden stellingen, en aan
het slot van het boek geven we de meetkundige [bewijzen der genoemde stellingen]."
(vertaling van Prof. Dr. Hk. de Vries: Historische Studiën, Deel 1, P. Noordhoff, Groningen, 1926):
Archimedes' bewijs
(We volgen hieronder de beschrijving van Sir T. Heath: A History of Greek Mathematics,
Volume II, Dover Publications, New York, 1981, in vertaling)
Zij ABC het bedoelde segment, BD de 'diameter', CF de raaklijn in C. Zij P een willekeurig punt van de boog van het segment, en AKF, OPNM evenwijdig met BD. Verbind nu CB en verleng het lijnstuk dat dan MO snijdt in N en FA in K. Zij verder KH = KC.
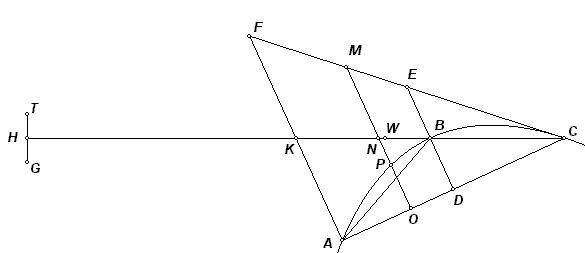
Nu geldt, volgens een 'eerder bewezen lemma':
| MO : OP | = CA : AO |
| = CK : KN | |
| = HK : KN |
Dus is, volgens de eigenschap van de parabool EB = BD, zodat MN = NO en FK = KA.
Wordt nu HC beschouwd als de arm van een balans, dan is TG, gelijk aan PO en geplaatst met
het midden in H, in evenwicht, rond K, met de lijn MO, met het midden in N.
Op dezelfde manier geldt dit voor alle lijnen, zoals MO en PO, in driehoek CFA in
relatie tot het segment CBA.
En er is een zelfde aantal van deze lijnen. Dus het gehele paraboolsegment, geplaatst bij
H, is in evenwicht met driehoek CFA.
Het zwaartepunt van driehoek CFA ligt in W, waarbij CW = 2 WK [en de gehele driehoek kan
worden opgevat als liggend in W].
Zodat
(segment ABC) : DCFA = WK :
KH = 1 : 3
Dus
(segment ABC) = 1/3 DCFA
= 4/3 DABC
Hetgeen te bewijzen was. ¨