Parabool: meetkundige eigenschappen en constructies (3)

Overzicht ][ Kegelsneden | Anal. meetkunde | Cabri ]

Overzicht

[ Pagina 1 ] [ Pagina 2 ] [ Pagina 3 ] [ Pagina 4 ]

Raakkoorde en middellijn
Opnieuw: constructies
Evenredige stukken op raaklijnen
Constructie met een cirkel
e.v. Zie pagina 4

10. Raakkoorde en middellijn

Definitie
Een raakkoorde van een parabool is het verbindingslijnstuk tussen de raakpunten van twee raaklijnen uit een punt aan de parabool.
of
Een raakkoorde is het verbindingslijnstuk tussen de raakpunten op de poollijn van een punt. Dat punt heet ook wel pool van de raakkoorde

Stelling 11a
De middens van evenwijdige raakkoorden van een parabool liggen op een lijn die evenwijdig is met de as van de parabool.

Bewijs:

De raaklijnen in de punten P₁, P₂ snijden elkaar in P.
De lijn door P // paraboolas snijdt die richtlijn in het midden H van R₁R₂, daar PR₁R₂ een gelijkbeninge driehoek is.
PH snijdt P₁P₂ in M_P.
Te bewijzen: M_P is het midden van P₁P₂.
Bewijs: P₁R₁R₂P₂ is een rechthoekig trapzium. PH // P₁R₁, dus MP is het midden van P1P2.

De cirkels P₁, P₂ (beide door F) hebben een gemeenschappelijke raaklijn R₁R₂.
Te bewijzen: HF _|_ P₁P₂.
Bewijs: H is het midden van R₁R₂. H heeft dus gelijke machten tov. beide cirkels. HF is dus de machtlijn van die cirkels. HF staat dus loodrecht op de centraal P₁P₂ van de cirkels.

Zij Q₁Q₂ een (willekeurige) koorde // P₁P₂.
Te bewijzen: het midden M_Q van Q₁Q₂ ligt op PH.
Bewijs: H is eveneens het midden van het raaklijnstuk aan de (niet getekende) cirkels door F met Q₁, Q₂ als middelpunt. HF staat ook loodrecht op Q₁Q₂. De raaklijnen in Q₁, Q₂ aan de parabool snijden elkaar dus eveneens op de lijn PH. M_Q ligt dus op PH.

Hiermee is de stelling bewezen. ¨

Gevolgen

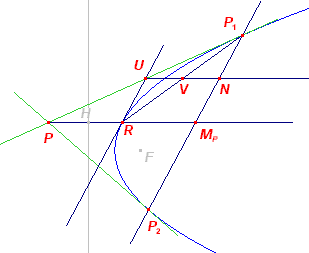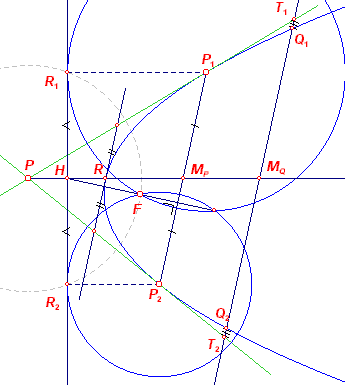
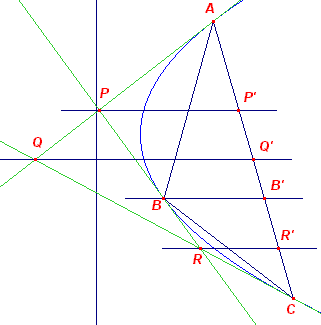
[1] Snijdt de koorde Q₁Q₂ de raaklijnen uit P in opvolgend T₁ en T₂, dan is dus ook Q₁T₁ = Q₂T₂ (zie figuur hierboven).

[2] De middelloodlijn van FH is eveneens raaklijn aan de parabool. Het raakpunt R ligt dus eveneens op PH en ook raaklijn in R // P₁P₂.
Merk nu op, dat PR = RM_P.
Bewijs:
De loodlijn door U (het snijpunt van de raaklijn in R met een raaklijn uit P) op de richtlijn deelt P₁R middendoor in V; immers UR en UP₁ zijn raaklijnen aan de parabool uit U (Stelling 11a).
UV snijdt PM_P in N. N is dan het midden van PM_P (middenparallel).
Dus UR = ½PM_P, zodat PR = RM_P. ¨

[einde Gevolgen]

Definitie
De meetkundige plaats van de middens van evenwijdige koorden van een parabool heet middellijn van die parabool.

We kunnen Stelling 11a ook iets anders formuleren:

Stelling 11b
Een middellijn van een parabool is de verzameling van de polen met evenwijdige raakkoorden (poolijnen)

Bewijs:

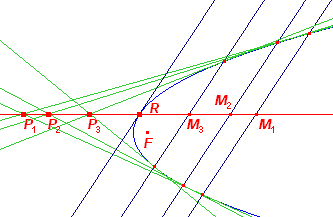Er is slechts een middellijn door R. Elk van de middens M_i van zo'n raakkoorde geeft een lijn M_iR die evenwijdig is met de as van de parabool.
De middellijn gaat ook door de pool van de betreffende koorde.
Alle lijnen MiR vallen dus samen. ¨

Opmerking
De raaklijn in R heet wel de aan die middellijn toegevoegde raaklijn.
[einde Opmerking]

Klik hier >< voor een CabriJavapplet die Stelling 11b illustreert.

11. Opnieuw: constructies

Constructie 15
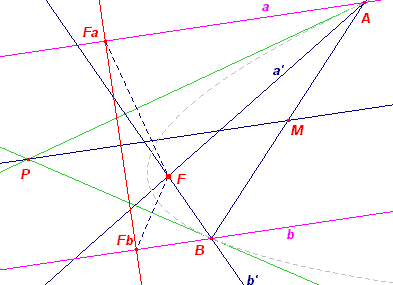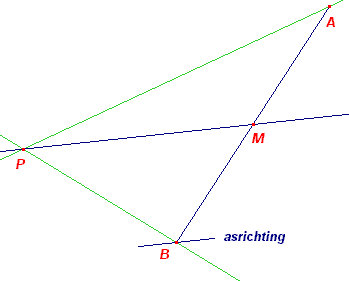
	Gegeven: twee punten A en B van de parabool (F, r), en de raaklijnen in die punten Te construeren: F en r Constructie: De lijn die het snijpunt P met het midden M van AB verbindt is een lijn evenwijdig aan de as (heeft de asrichting). De voerstralen van A en B maken met de asrichting een hoek die gelijk is aan die de raaklijn met de asrichting maakt. De voerstralen zijn dus construeerbaar als spiegbeelden a' en b' van de lijnen a en b door A en B evenwijdig met de asrichting F is het snijpunt van a' en b'. De lijn door de spiegelbeelden Fa en Fb van F in de raaklijnen is de richtlijn. ¨ ¤ Zie ook Paragraaf 12: Evenredige stukken op raaklijnen.
Constructie 16
	Gegeven: Twe punten A en B, de raaklijn in A en de asrichting (via een lijn, bijvoorbeeld door B). Te construeren: F en r Constructie: Het snijpunt P van de raaklijnen in A en B ligt op de lijn door M (het midden van AB) die evenwijdig is met de as. PB is de tweede raaklijn. Hiermee is de constructie teruggebracht tot Constructie 15. ¨ Opmerking Een bijzonder geval krijgen we als gegeven zijn: de top, de as(richting) en een tweede punt. Immers hiermee is ook de topraaklijn bekend. [einde Opmerking]
Constructie 17a
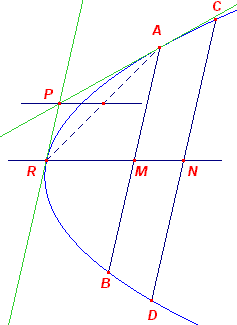
	Gegeven: een in ligging gegeven parabool ('in ligging gegeven' betekent: elk punt van de parabool kan worden getekend) Te construeren: F en r Constructie: We kiezen twee willkeurige evenwijdige koorden AB en CD. De middens M en N van die koorden bepalen de asrichting (MN is een middellijn). De raaklijn in het snijpunt R van deze middellijn en de parabool is evenwijdig met de koorden AB en CD. Nu zijn bekend: een punt R en daarin de raaklijn, een tweede punt (bijvoorbeeld A) en de asrichting. Deze constructie is daardoor teruggebracht tot Constructie 16. ¨ Opmerking Zie Constructie 17b voor een andere manier van uitvoering. [einde Opmerking]
Constructie 17b
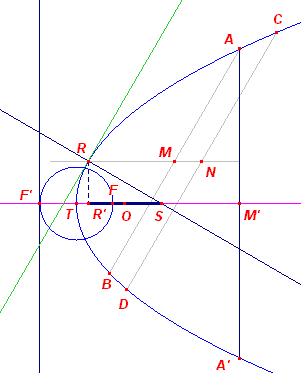
	Constructie: Is de asrichting MN bekend, dan construeren we een koorde AA' loodrecht op MN. Het midden M' van AA' ligt op de as. De paraboolas is dus construeerbaar als de lijn door M' evenwijdig met MN. Dit geeft tevens de top T van de parabool. De lijn in R loodrecht op de raaklijn in R (deze raaklijn is evenwijdig met AB) snijdt de as in het punt S. Zij nu T de projectie van R op de as. Dan is ST gelijk aan de parameter p van de parabool. De cirkel (T, ½p) snijdt nu de as in de punten F (het brandpunt) en F' (het snijpunt van de richtlijn met de as). ¨

12. Evenredige stukken op raaklijnen

Stelling 12
Elke raaklijn bepaalt op twee andere raaklijnen evenredige stukken.

Bewijs:

parab3-st12

De raaklijnen in A, B, C snijden elkaar in P, Q, R (zie figuur hiernaast).
We zullen aantonen: AP : PQ = PB : BR = QR : RC
We tekenen de middllijnen door P, Q, R; deze delen de bijbehorende raakkoorden middendoor.
Tekenen we ook de middellijn door B, dan vinden op de koorde AC drie tweetallen van gelijke stukken, te weten:
   AQ' = Q'C; AP' = P'B'; CR' = R'B"
Verder is:
   AC = AB' + B'C
zodat ½AC = ½AB' + ½B'C, waaruit: AQ' = AP' + B'R', wat geeft: AQ' - AP' = B'R'
   P'Q' = B'R'
En dan ook:
   P'B' = Q'R'
Nu is:

AP : PQ = AP' : P'Q'	PB : BR = P'B' : B'R'	QR : RC = Q'R': R'C
Hierin zijn de tweede leden telkens aan elkaar gelijk. De eerste leden dus ook. ¨

Constructie 18
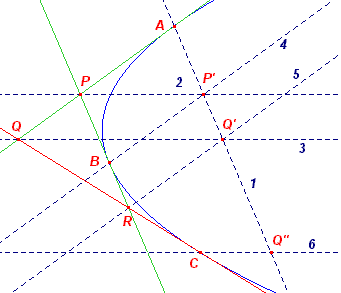
	Op basis van Stelling 12 kunnen we nu uitgaande van twee raaklijnen en hun daarop gelegen raakpunten een derde punt (en z'n raaklijnen construeren. En daarmee wederom de omhullenden van de parabool. Gegeven: raaklijnen in A en B (snijdend in P) Te construeren: een punt C met de raaklijn in C Constructie: Kies op het verlengde van AP een punt Q en bepaal op PB een punt R zo, dat AP : PQ = PB : BR. Dan is QR een raaklijn aan de parabool in het punt C, waarvoor geldt: AP : PQ = QR : RC In de constructie zijn opvolgend de lijnen 1, ..., 5 gebruikt.Vervolgens is Q" het Q'-spiegelbeeld van A. De lijn 6 // lijn 3 geeft dan het punt C. ¨
	Opmerkingen [1] Voor een eenvoudiger constructie van een "willekeurige" raaklijn kan Q zo worden gekozen, dat AP = PQ. [2] Om meerdere raaklijnen en raakpunten te construeren kunnen AP en BP in een gelijk aantal stukken worden verdeeld. Deze gelijke stukken worden ook op de verlengden van AP en PB afgezet. De verbindingslijnen van overeenkomstige deelpunten zijn dan de raaklijnen. De raakpunten kunnen dan eveneens via de vaste verhoudingen (met twee evenwijdige lijnen) worden gevonden (zie de figuur hiernaast).. [einde Opmerkingen]

13. Constructie met een cirkel

Stelling 13
Een parabool kan worden voortgebracht via een variabel punt op een cirkel.

Klik hier >< voor een CabriJavapplet bij Stelling 13.

Bewijs:
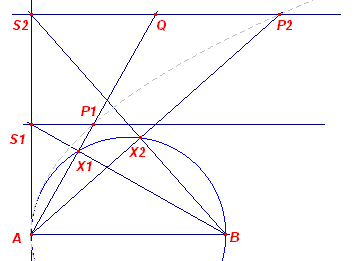
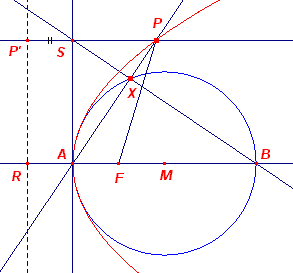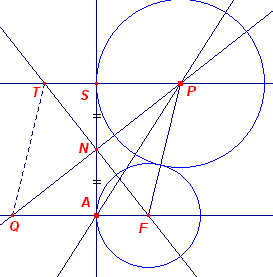
	In nevenstaande figuur is X een variabel punt op de cirkel met middellijn AB (middelpunt M). De raaklijn in A en de lijn BX snijden elkaar in S. De loodlijn in S op AS snijdt AX in P. Nu is P een punt van een parabool met brandpunt F, waarbij F het midden is van AM. Immers, ABS ~ SAP, zodat AS : SP = AB : SA, waaruit AS² = AB · SP (te gebruiken in Constructie 20) Of AS² = 4AF · PS Maar ook: AS² = PF² - (PS - AF)² Waaruit we vinden: PF² - (PS - AF)²= 4PS · AF, zodat PF2 = (PS + AF)² of PF = PS + AF Dus P ligt op een parabool met brandpunt F en richtlijn R'P'. ¨
Constructie 19
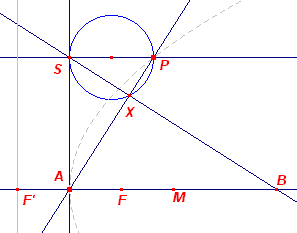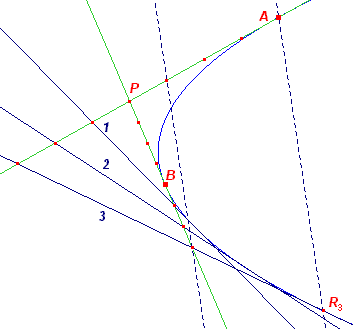
	Gegeven: as, top A en een willekeurig punt P van parabool (F, r) Te construeren: F (en r) (1) Constructie: (op basis van Stelling 13) De topraaklijn kan worden geconstrueerd. De projectie van P daarop is S. Het punt X ligt op de cirkel met middellijn PS. Het punt X is het snijpunt van AP en die cirkel. Waarmee opvolgend B, F (en F', en de richtlijn) gevonden worden. ¨
	(2) Constructie: (op basis van PF = PS + AF) Het punt F ligt zo op de as, dat de cirkel (F, FA) raakt aan de cirkel P, PQ). Hiermee is de constructie teruggebracht tot het Raakprobleem van Apollonius (A111). Hiernaast staat een eenvoudiger constructie van het punt F (eenvoudiger dan de constructie A111, omdat A op de lijn ligt, en die lijn ook raaklijn is). N is het midden van AS. NF staat loodrecht op PN. De cirkel (F, FA) raakt nu aan cirkel P. Immers, FPTQ is een ruit, zodat PF = FA + AQ = FA + PS. ¨

Constructie 20
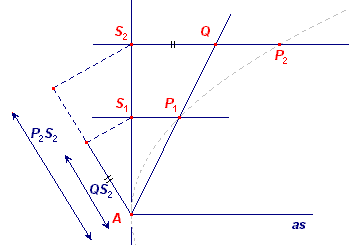
	Gegeven: as, top A en een willekeurig punt P₁ van de parabool (F, r) Te construeren: een tweede punt P₂ van de parabool Analyse: Gaan we uit van twee punten P₁ en P₂ (het tweede punt) van de parabool, dan hebben we (zie Stelling 13): AS₁² = AB · P₁S₁ AS₂² = AB · P₂S₂ De lijn AP₁ snijdt P₂S₂ in Q. Dan is ook: AS₁ : P₁S₁ = AS₂ : QS₂ We vinden dan: AS₁ : AS₂ = QS₂ : P₂S₂ ¨
	Constructie: Uitgaande van het punt P₁ (en dus ook S₁) kunnen we een tweede punt P₂ construeren door op de topraaklijnn een punt S₂ te kiezen en dan allereerst het punt Q te construeren als snijpunt van de loodlijn in S₂ en de lijn AP₁. Het punt P₂ vinden we dan uit de evenredigheid AS₁ : AS₂ = QS₂ : P₂S₂. ¨ Zie verder onderstaande Opmerking.
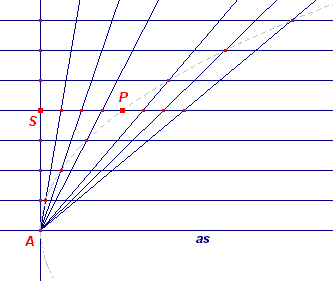
	Opmerking Om meerdere punten van de parabool te vinden verdelen we AS en PS in eenzelfde aantal gelijke stukken. Deze stukken zetten we dan ook af op het verlengde van SP en op het verlengde van AS. Door de deelpunten te verbinden met A en elk van deze verbindingslijnen te snijden met de overeenkomstige lijn // de paraboolas vinden we andere punten van de parabool. [einde Opmerking]

[ Pagina 1 ] [ Pagina 2 ] [ Pagina 3 ] [ Pagina 4 ]

[parab3.htm] laatste wijziging op: 16-11-03