Parabool: meetkundige eigenschappen en constructies (2)

Overzicht  ][  Kegelsneden | Anal. meetkunde | Cabri ]

Overzicht terug

[ Pagina 1 ] [ Pagina 2 ] [ Pagina 3 ] [ Pagina 4 ]

  1. Poollijn van een punt / raaklijnen uit een punt
  2. Raaklijn evenwijdig met een lijn
  3. De driehoek gevormd door drie raaklijnen aan een parabool
          (met oa. Simson-lijn en Steiner-lijn)
  4. Vier raaklijnen aan een parabool
  5. Omhullende raaklijnen cabrisignal
  6. e.v. Zie Pagina 3

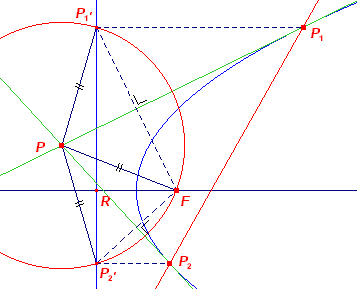
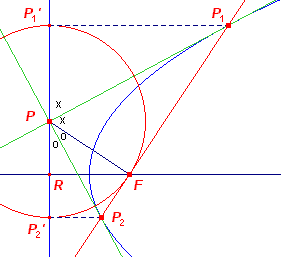
5. Poollijn van een punt / raaklijnen uit een punt terug

Definitie (gedeeltelijk)
De poollijn van een punt (buiten de parabool) is de verbindingslijn van de raakpunten van beide raaklijnen uit dat punt aan de parabool.
Constructie 11 (eerste methode, met richtlijn)
parab21 In nevenstaande figuur is de poollijn van P tov van de parabool (F, r) getekend.
De punten P1' en P2' zijn de spiegelbeelden van F in de beide raaklijnen.
Nu is vanwege de symmetrie:
PF = PP1' = PP2'
De punten P1' en P2' liggen dus op de cirkel (P, PF).
De constructie van de poollijn van P (buiten de cirkel), te weten de lijn P1P2, is hiermee eenvoudig uit te voeren.
Daarmee is tevens de constructie van de beide raaklijnen uit een punt aan de cirkel gegeven. ¨
            parab22 Ligt het punt P op de richtlijn, dan verloopt de constructie analoog.

Gevolg
P1PP2 = 90º, immers de raaklijnen zijn in dit geval de bissectrices van FPP1' en FPP2'.
We hebben dan:

Stelling 6
De richtlijn van een parabool is de meetkundige plaats van de snijpunten van loodrecht op elkaar staande raaklijnen aan die parabool.

Opmerking - De richtlijn heet daarom ook wel orthoptische lijn.

Hierboven is de richtlijn gebruikt. We kunnen ook de topraaklijn gebruiken.

Constructie 12 (tweede methode, met topraaklijn)

parab23

 We bekijken de cirkel op PF.
Deze cirkel snijdt de topraaklijn in de punten S1 en S2.
PS1 en PS2 zijn dan de raaklijnen uit P aan de parabool, immers de beelden P1' en P2' van F in de punten Si liggen dan op de richtlijn.
De raakpunten Pi vinden we als snijpunten van de loodlijnen in Pi' en de raaklijnen.
¨

 

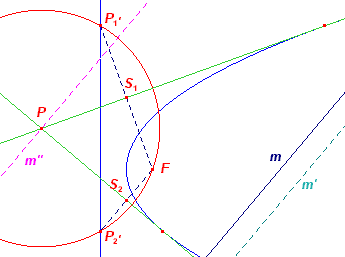
6. Raaklijn evenwijdig met een lijn terug
In Constructie 4 (op Pagina 1) is de constructie gegeven van een raaklijn evenwijdig met een lijn m.
Deze constructie is gebaseerd op spiegeling van het punt F in de raaklijn.
We kunnen dit probleem echter terugvoeren op het construeren van raaklijnen uit een punt aan de parabool, mits we dat punt kiezen als oneigenlijk punt van de lijn m.

figuur a figuur b
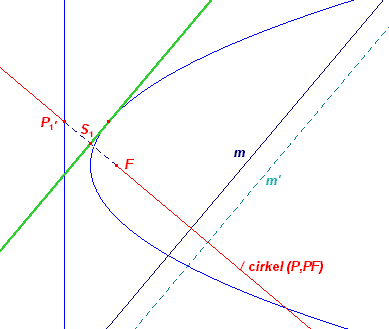   parab24    parab24b

In figuur a zijn de raaklijnen uit P aan de parabool (F, r) getekend, op basis van Constructie 11.
In die figuur wordt het oneigenlijk punt van m vastgelegd door de evenwijdige lijnen m en m'.
We 'verplaatsen' nu P over de lijn m" (de lijn door P evenwijdig met m) naar het oneigenlijk punt van m.
In figuur b zien we dan dat daarmee een raaklijn evenwijdig met m aan de parabool wordt geconstrueerd (door het punt S1).
Opmerking
De tweede raaklijn uit P is dan de oneigenlijke rechte.
[einde Opmerking]

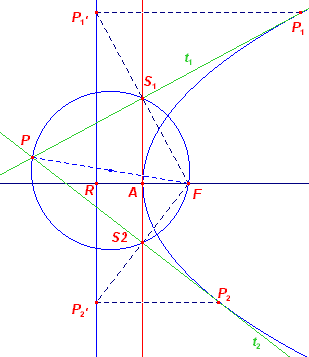
7. De driehoek gevormd door drie raaklijnen aan een parabool terug
We bewijzen allereerst:

Stelling 7
7.1.
De hoekgevormd door de voerstralen van de raakpunten der raaklijnen door een punt wordt middendoor gedeeld door de verbindingslijn van dat punt en het brandpunt.
7.2.
De hoek tussen de asrichting en een raaklijn uit een punt aan een parabool is gelijk aan de hoek tussen de andere raaklijn en de verbindingslijn tussen dat punt en het brandpunt.
Bewijs van 7.1:
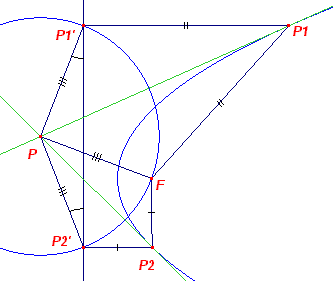parab25a De raaklijnen zijn geconstrueerd op basis van Constructie 11.
Nu is PP1'P2' een gelijkbenige driehoek.
Dus
   PP1'P2' = PP2'P1'
Voorts is P1P1'P2' = P2P2'P1' = 90º
Zodat in de vliegers P1P1'PF en P2P2'PF geldt:
   PFP1 = PFP2
Hetgeen bewezen moest worden. ¨
Bewijs van 7.2:
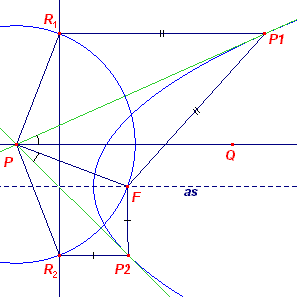parab25b PQ is de lijn door P // paraboolas.
We dienen aan te tonen, dat P1PQ = P2PF.

Nu is R1PQ = R2PQ (gelijkbenige driehoek R1PR2).
Zodat

2(P1PQ) = 2(P1PF - FPQ) = R1PF - 2 (FPQ) = (R1PF - FPQ) - FPQ
= R1PQ - FPQ
= R2PQ - FPQ = R2PF
= 2 (P2PF)

Hetgeen bewezen moest worden. ¨

Opmerking
Stelling 7.2 kan ook geformuleerd worden als:

Stelling 7.2b
PQ en PF liggen symmetrisch tov. de bissectrice van P1FP2.

[einde Opmerking]

Stelling 8
De omcirkel van de driehoek die gevormd wordt door drie raaklijnen aan een parabool, gaat door het brandpunt van die parabool.
Bewijs:
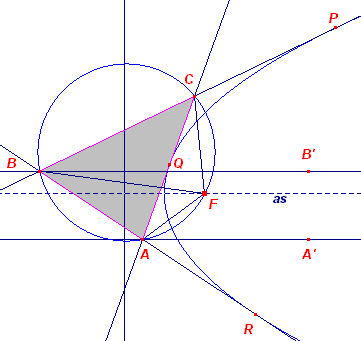parab26 In P, Q, R zijn de raaklijnen aan de parbool (F, R) getekend.
Zij AA' en BB' lijnen evenwijdig met de asrichting van de parabool.
Dan is (op grond van Stelling 7.2, kijkend naar de raaklijnen door punt A):
   FAC = RAA'
Evenzo (kijkend naar de raaklijnen door punt B):
   RBB' = FBC
Nu geldt, wegens BB' // AA':
   RBB' = RAA'
zodat
   FAC = FBC.
Volgens de Stelling van de omtrekshoek liggen zijn de driehoeken FAC en FBC dus in dezelfde cirkel beschreven.
Waarmee het gestelde is aangetoond. ¨

Opmerking
Zie verder ook Paragraaf 9: Omhullende raaklijnen
Zie ook Paragraaf 12: Evenredige stukken op raaklijnen.
[einde Opmerking]
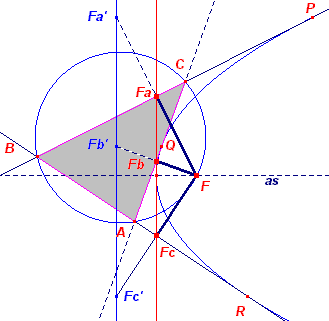parab27                      Gevolg: Simson-lijn en Steiner-lijn terug
We weten, dat de voetpunten van de loodlijnen uit F neergelaten op de raaklijnen op de topraaklijn liggen (zie Stelling 4a, pagina 1).
Dus de punten Fa, Fb, Fc. liggen op de topraaklijn van de parabool.
De topraaklijn is de Simson-lijn van het punt F bij driehoek ABC (zie de pagina "De lijn van Simson", Stelling 2).
De richtlijn van de parabool is dan de Steiner-lijn van het punt F bij driehoek ABC (zie de pagina "De lijn van Steiner").
Voorts, bij elk punt F van de omcirkel van driehoek ABC kunnen we een parabool vinden, die raakt aan de zijden van ABC, zodat we hier een ander bewijs van de volgende stelling gevonden hebben:
Stelling 9
De voetpunten van de loodlijn op de zijden van een driehoek, neergelaten uit een punt van de omcirkel, zijn collineair.

Zie verder ook de pagina "De lijn van Steiner".

8. Vier raaklijnen aan een parabool terug

Constructie 13
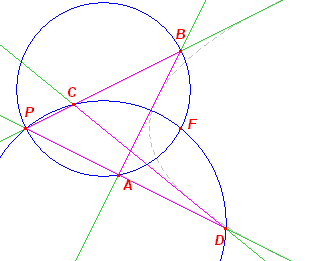parab29 Gegeven: vier raaklijnen aan een parabool
Te construeren: het brandpunt (en de richtlijn)
Constructie:
We kiezen de driehoeken PAB en PCD, waarvan we de omcirkel bepalen.
Het van P verschillend snijpunt van deze cirkels is het brandpunt F van de parabool.
Bewijs: Zie Stelling 8. ¨

Opmerking
Zie ook "Pagina 5": Gebruik van oneigenlijke punten, Constructie 22.
[einde Opmerking]

9. Omhullende raaklijnen terug

Uit Stelling 8 volgt:

Stelling 10
Het lijnstuk op een raaklijn, tussen de snijpunten met twee andere raaklijnen wordt vanuit het brandpunt gezien onder een constante hoek.
Bewijs:
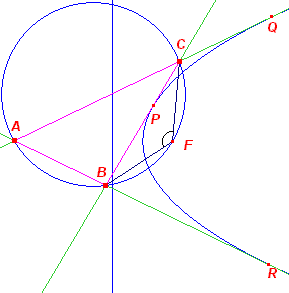parab30 F ligt op de omcirkel van ABC (zie Stelling 8). Volgens de stelling van de omtrekshoek is dan:
   BFC = ½bg(180 - A)
Hetgeen te bewijzen was. ¨

Deze stelling heeft een bijzonder gevolg. Zie Constructie 14.

 
Constructie 14a Klik hier >Animatie< voor een CabriJavapplet hierbij.
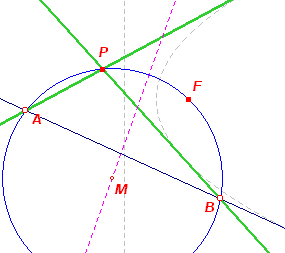parab30b parabc14 Gegeven zijn twee raaklijnen aan de parabool. Ook het brandpunt is gegeven.
Zij P het snijpunt van deze raaklijnen.
We beschouwen vervolgens alle cirkels door P en F (middelpunten op de middelloodlijn van PF).
A en B zijn de van P verschillende snijpunten van zo'n cirkel (met middelpunt M) met de gegeven raaklijnen.
De lijn AB is dan (volgens Stelling 10) een raaklijn aan de parabool.
De parabool wordt dan door de lijnen AB omhuld als M de middelloodlijn van PF doorloopt. ¨

Gevolg - P op de parabool-as

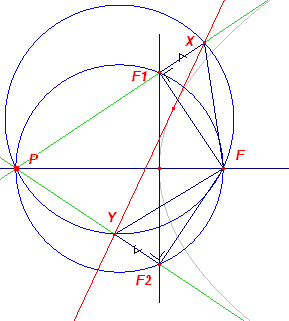parab2-c11a Door P op de as zijn twee raaklijnen gegven. Een derde raaklijn snijdt die raaklijnen in X en Y.
F1 en F2 zijn de projecties van F op die raaklijnen (F1F2 is dan de topraaklijn).
Nu is:
FPF1 = FPF2 en F1F = F2F (symmetrie).
Voorts liggen P, X, Y, F op een cirkel (de omcirkel van PXY; zie Stelling 10).
Dus XF = YF.
Zodat XFF1 en YFF2 congruent zijn. En daaruit volgt dan:
   F1X = F2Y

We kunnen de parabool  omhullen met raaklijnen als er naast het brandpunt twee (elkaar, dit keer, op de as snijdende) raaklijnen gegeven zijn (zie Constructie 14a).
Maar het kan nu ook op een andere manier.
Constructie 14b Klik hier >Animatie< voor een CabriJavapplet hierbij.
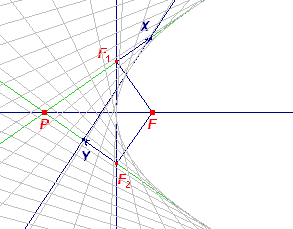parab2-c11b We bepalen de projecties F1 en F2 van F op beide raaklijnen.
Vanuit F1 en F2 kiezen we op die raaklijnen (aan weerskanten van F1F2) de punten X en Y met XF1 = YF2.
De lijn XY is dan omhullende van de parabool. ¨

[ Pagina 1 ] [ Pagina 2 ] [ Pagina 3 ] [ Pagina 4 ]

begin pagina
[parab2.htm] laatste wijziging op: 21-12-03