De lijn van Steiner

Overzicht  ][  DK & meetkunde

Zie ook het Cabri-werkblad "De lijn van Simson"
Zie ook de pagina "Meer bijzonderheden van de Simson-lijn"

Overzicht

  1. Een eerste kennismaking met het probleem
  2. Bewijs
  3. De parabool en de lijn van Steiner
       3.1. Inleiding
       3.2. Hoofdeigenschap van de raaklijn
       3.3. Parabool, driehoek, lijn van Steiner
       3.4. De Euler-lijn als Steiner-lijn, Kiepert-parabool

1. Een eerste kennismaking met het probleem terug
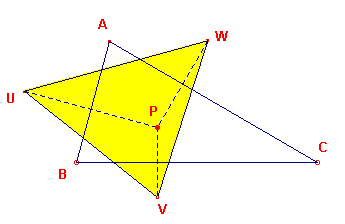
We gaan uit van een driehoek ABC en een willekeurig punt P.
We bepalen de symmetriepunten U, V, W van P ten opzichte van de zijden AB, BC, CA van de driehoek. In het algemeen zullen de punten U, V en W een driehoek insluiten (zie figuur 1).

figuur 1 figuur 1 We vragen ons nu af of het mogelijk is de positie van het punt P zo te bepalen, dat de punten U, V, W collineair zijn (op dezelfde drager liggen).

|§| Klik hier Animatie om dit onderzoek via een animatie te verrichten.

Uit het onderzoek via de animatie kunnen we concluderen

Stelling 1
Ligt een punt P op de omgeschreven cirkel van een driehoek, dan liggen de gespiegelden van dat punt P in de zijden van die driehoek op een rechte lijn.
Deze rechte lijn heet de lijn van Steiner van het punt P.

Jakob Steiner (1796-1863, Zwitserland) wordt wel beschouwd als de grondlegger v an de projectieve meetkunde. Hij bewees onder meer de stelling (genoemd naar Steiner en Poncelet), dat alle euclidische constructies met een (ongemerkte) liniaal kunnen worden uitgevoerd als er een vaste cirkel gegeven is.

Maar we kunnen verder onderzoeken.
Het blijkt dat de lijnen van Steiner bij een vaste driehoek door een bijzonder punt van die driehoek gaan.
|§| Klik hier Animatie om ook dit onderzoek via een animatie te verrichten.

We hebben nu dus gevonden

Stelling 2
De lijn van Steiner van een punt van de omcirkel van een driehoek gaat door het hoogtepunt van die driehoek.

Natuurlijk is het een goede zaak de gevonden resultaten ook daadwerkelijk te bewijzen. Dat zullen we doen in de volgende paragraaf.

2. Bewijs terug

Bij het bewijs van de in paragraaf 1 genoemde eigenschappen van de lijn van Euler, zullen we gebruik maken van de lijn van Simson.

figuur 2 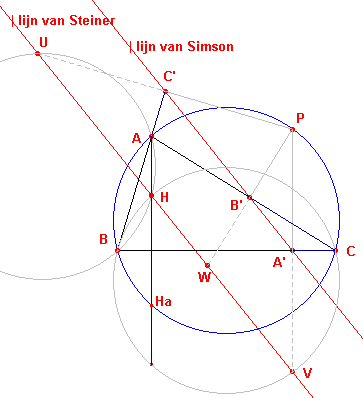imagessteinerh Bewijs van stelling 1

De lijn van Simson wordt geconstrueerd door van een punt P op de omgeschreven cirkel de voetpunten te bepalen van de loodlijnen op de zijden van de driehoek (zie figuur 2).
De bedoelde punten zijn hier A', B', C'.
De punten A', B', C' liggen dus op een rechte lijn (de lijn van Simson)

De punten U,V,W zijn de gespiegelden van P in de zijden, dus A', B', C' zijn de middens van de lijnstukken PV, PW en PU.

Kiezen we nu een vermenigvuldiging met factor 2 en centrum P, dan wordt de lijn van Simson (samen met de punten A', B', C') afgebeeld op een daarmee evenwijdige lijn, de lijn van Steiner (samen met de beeldpunten V, W, U).

Hiermee is stelling 1 bewezen. ¨

Bewijs van stelling 2

We verlengen de hoogtelijn uit A tot deze de omgeschreven cirkel snijdt in het punt Ha.
We kunnen nu bewijzen, dat H en Ha symmetrisch liggen ten opzichte van de lijn BC (klik hier hier voor het bewijs)..
Wanneer we de omgeschreven cirkel spiegelen in de zijden van de driehoek gaan deze cirkels dus door het punt H.

In figuur 2 is de omgeschreven cirkel gespiegeld in de zijden BC en AB.
De punten B, V, C en H liggen dus op een cirkel; dat is dus ook het geval met de punten A, U, B en H.
Nu is dus ÐBHV = ÐBCV (staan op dezelfde boog).
En ook ÐBHU = ÐBAU (staan op dezelfde boog). Optelling geeft dan
ÐVHU = ÐBHV + ÐBHU = ÐBCV + ÐBAU (we willen graag dat deze hoek, ÐVHU, gelijk is aan 180º ! )
Wegens de symmetrie is ÐBCP = ÐBCV en ook ÐPAB = ÐBAU, zodat
ÐVHU = ÐBCP + ÐPAB = ½bg(PAB) + ½bg(BCP) = 180º.
Dus ligt H op de lijn van Steiner.

Hiermee is dus stelling 2 bewezen. ¨

Opmerking
Een iets ander bewijs van Stelling 2 vinden we op de pagina "Meer bijzonderheden van de Simson-lijn".
[einde Opmerking]

3. De parabool en de lijn van Steiner terug

3.1. Inleiding terug
In deze paragraaf leggen we een verband tussen een parabool en de lijn van Steiner (dus daardoor ook tussen die parabool, een driehoek en de omgeschreven cirkel van die driehoek).
|§| Klik hier Animatie om (nog eens) te kijken naar de definitie van de parabool als meetkundige plaats van punten die een bepaalde eigenschap hebben.

De gebruikelijke (meetkundige) definitie van een parabool is dus

Definitie
De meetkundige plaats (verzameling) van de punten P die gelijke afstand hebben tot een vast punt F en een vaste lijn r is een parabool.
Het punt F heet het brandpunt (focus) van de parabool; de lijn r heet de richtlijn (directrix); de lijn door F loodrecht op r heet de as.

3.2. Hoofdeigenschap van de raaklijn terug
In elk punt van een parabool kan een raaklijn aan die parabool getekend worden.
|§| Klik hier Animatie om de (hoofd)eigenschap van de raaklijnen te onderzoeken.

Stelling 3a (hoofdeigenschap van de raaklijn)
De raaklijn in aan punt P aan een parabool is bisectrice van de hoek tussen de lijn door P en het brandpunt en de lijn door P loodrecht op de richtlijn.

Stelling 3b
Het spiegelbeeld van het brandpunt in een raaklijn ligt op de richtlijn van die parabool.

Klik hier voor een elementair bewijs van de stelling 3a en 3b.

3.3. Parabool, driehoek, lijn van Steiner terug
Nu we dit laatste (stelling 3b) weten kunnen we in drie punten T1, T2, T3 raaklijnen aan een parabool met brandpunt F en richtlijn r tekenen.
Deze raaklijnen snijden elkaar twee aan twee in de punten A, B, C.

We gaan nu driehoek ABC, en in het bijzonder de ligging van de lijn van Steiner met betrekking tot die driehoek, onderzoeken.

Voordat we dat doen merken we echter op, dat het punt F op de omgeschreven cirkel van driehoek ABC moet liggen.
Ga dat (zonodig) na met behulp van stelling 1.
|§| Klik hier >Animatie< om het onderzoek naar de samenhang tussen driehoek ABC en de lijn van Steiner.

Als het goed is, hebben we uit het laatste onderzoek datgene geconcludeerd wat in stelling 4 (hieronder) is geformuleerd.

figuur 3 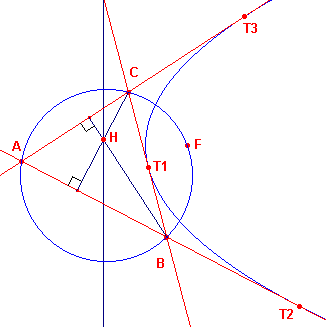imagessteiner2 We kunnen nu eenvoudig bewijzen (zie figuur 3)
Stelling 4
Het hoogtepunt van driehoek ABC ligt op de richtlijn r van de parabool.

Bewijs:
Uit stelling 3b volgt, dat de drie spiegelbeelden van F in de drie raaklijnen op een rechte lijn (de lijn r liggen).
Het punt F ligt ook op de omgeschreven cirkel van driehoek ABC (zie stelling 1).
Maar dan is r dus de lijn van Steiner van het punt F bij deze driehoek.
r gaat dus door het hoogtepunt van driehoek ABC (zie stelling 2). ¨ 

Ook de omgekeerde stelling geldt
Stelling 5
Is ABC een driehoek en F een punt van de omgeschreven cirkel van die driehoek (niet zijnde A, B of C), dan raakt de parabool met brandpunt F en met de lijn van Steiner van F als richtlijn aan de drie zijden van die driehoek.

Klik hier >Applet< voor een CabriJavapplet bij Stelling 5.

3.4. De Euler-lijn als Steiner-lijn, Kiepert-parabool terug
Er is een punt F van de omcirkel waarvoor de bijbehorende Steiner-lijn door het middelpunt van de omcirkel gaat.
In dit geval valt de Steiner-lijn van F dus samen met de Euler-lijn van de driehoek.

|§| Klik hier >Applet< om de positie van dat punt F te onderzoeken.

We geven nu als definitie

Definitie
De parabool die raakt aan de zijden van de driehoek en waarvan de richtlijn samenvalt met de Euler-lijn van de driehoek, heet Kiepert-parabool.

Opmerking
Het brandpunt van de Kiepert-parabool ligt volgens Stelling 5 op de omcirkel van de driehoek.
Dit punt wordt met aangeven met X110 (volgens Kimberling).
[einde Opmerking]

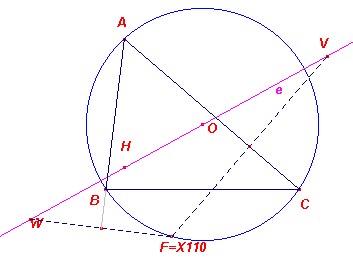steiner32 Uit de definitie van de Steiner-lijn volgt nu:
 
Gevolg
De spiegelbeelden V en W van X110 in opvolgend de zijden AC en AB liggen op de Euler-lijn.

Constructie van X110
Gegeven: driehoek ABC
Te construeren: X110
Constructie:

X110 Kiepert-parabool
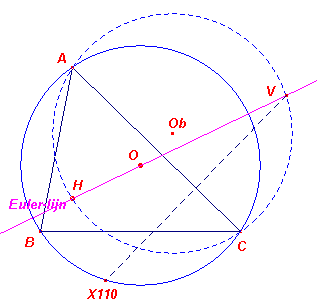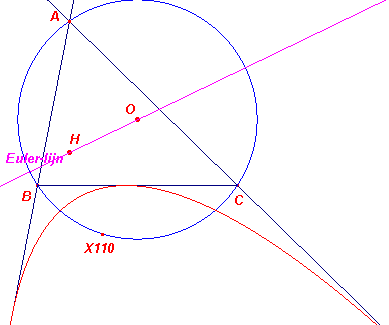
steiner4 Het punt F (X110) ligt op de omcirkel van ABC. Het punt V (het spiegelbeeld van F in AC) ligt dus op het spiegelbeeld van de omcirkel in AC.
Volgens het bovenstaande Gevolg is het spiegelbeeld van X110 in AC het snijpunt van het spiegelbeeld van de omcirkel in AC (middelpunt Ob) met de Euler-lijn van driehoek ABC.		 .steiner4b

Opmerking
We kunnen hierbovenstaand Gevolg ook als volgt formuleren:

Stelling 6
De gespiegelden van de Euler-lijn van een driehoek in de zijden zijn concurrent op een punt van de omcirkel van die driehoek.

begin pagina
[steiner.htm] laatste wijziging op: 27-12-2004