Cabri-werkblad
Overzicht ][ Alle werkbladen | Meetkunde | Cabri
Overzicht - De lijn
van Simson 
| figuur 1 |  |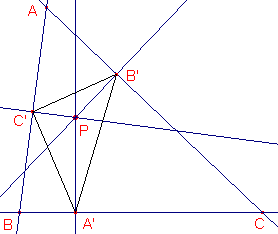
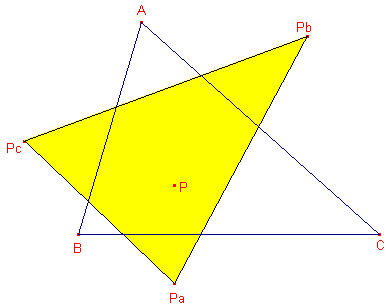
Teken op een nieuw werkblad drie
punten: A, B, C. Teken ook de lijnen AB, BC, CA. (Teken-menu: Lijn,  ). Teken nu een punt P (kies het punt P om te beginnen binnen driehoek ABC). Teken de loodlijnen uit P op BC (snijpunt A'), op CA (snijpunt B') en op AB (snijpunt A'). Teken vervolgens driehoek A'B'C' (Teken-menu: Driehoek,  ). |
Driehoek A'B'C' heet de
voetpuntsdriehoek van het punt P (tov. driehoek ABC). De hoekpunten van de driehoek heten de voetpunten van P (tov. driehoek ABC).Er zijn posities van het punt P waarvoor de drie zijden van A'B'C' samenvallen.
Maar er zijn nog andere posities van P.
2 Welke posities van P zijn dat? Geef een zo kort mogelijke beschrijving van je bevindingen.
Klik hier 
voor een CabriJavapplet bij Opdracht 1.
| figuur 2 |  |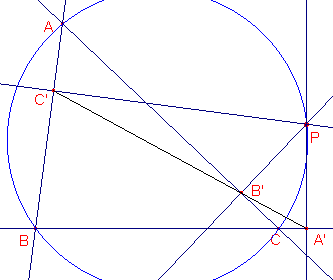
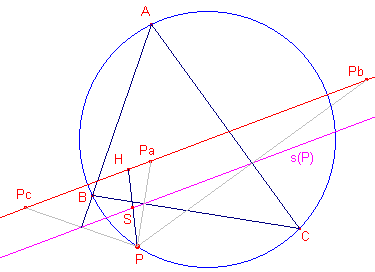
Teken ook de omcirkel van driehoek
ABC. Gebruik daarvoor eventueel de macro:Omcirkel3P. Herdefinieer nu het punt P op deze omcirkel. Dit gaat via de functie "Herdefinieer object",  , in het Constructie-menu.
Selecteer het punt P, kies uit het verschijnende menulijstje de functie "Punt op
object" en selecteer dan de omcirkel.Verplaats het punt P nu op die omcirkel. 2 Zijn je bevindingen in overeenstemming met die bij Opdracht 1? Zie ook de CabriJavapplet bij Opdracht 1. |
Selecteer de "voetpuntsdriehoek" (Deze driehoek) en druk op de [Del] toets.
Teken nu de lijn door de punten A' en B' (C' ligt er dan automatisch op).
• Bewaar deze figuur in een bestand (bijv.
onder de naam ‘startsimson.fig’).
De lijn heet
de lijn van Simson van het punt P (tov. de driehoek). We geven in hetgeen volgt deze lijn aan met s(P).Opmerking
Robert Simson (1687-1768, Schotland) heeft met de naar hem genoemde lijn helemaal niets van doen. De lijn is namelijk in 1797 ontdekt door een landgenoot van hem, William Wallace (1768-1843). De in de wiskundige literatuur meestal gebruikte naam is Simson-lijn (en niet Wallace-lijn). De lijn wordt ook wel voetpuntsrechte van P genoemd.
[einde Opmerking]
We hebben nu:
| Stelling 1 De voetpunten van een punt dat gelegen is op de omcirkel van een driehoek, liggen op een rechte lijn, de Simson-lijn van dat punt. |
We moeten deze stelling natuurlijk bewijzen.
De vraag is natuurlijk "hoe bewijs je dat drie punten op een lijn liggen (collineair zijn)?"
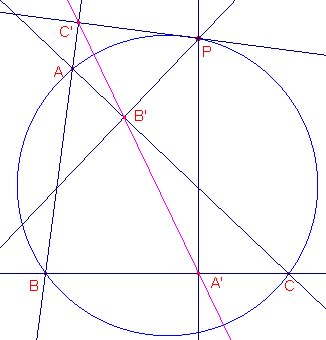
Kijk eens naar figuur 3a en merk op, dat het punt B' tussen A' en C' in ligt.
2 Als A', B', C' collineair zijn, hoe groot is dan ÐA'B'C'?
2 Als A', B', C' collineair zijn, wat is er dan te zeggen van de hoeken AB'C' en CB'A'?
Verklaar kort je antwoord.
We vervangen nu de eerder gesteld vraag door de opdracht – bewijs dat
ÐAB'C' = ÐCB'A' – .In figuur 3b hebben we nog twee lijnstukken, PA en PC, en twee cirkels toegevoegd.
| figuur 3a | figuur 3b |
 |
 |
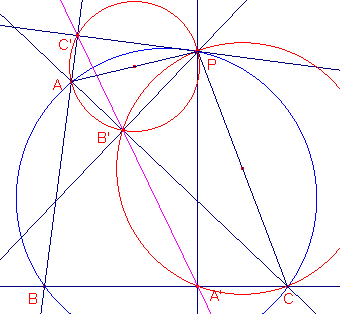2 Waarom zijn de vierhoeken AB'PC' en CPB'A' koordenvierhoeken?
2 Wat zijn de getekende cirkels van deze koordenvierhoeken?
In figuur 3b zijn nog twee andere koordenvierhoeken aan te wijzen.
2 Welke zijn dat?
| figuur 4 |  |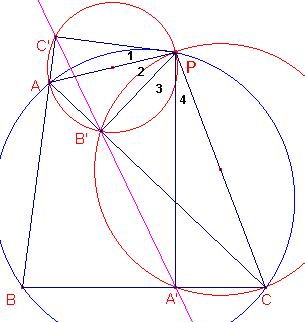
In figuur 4 zijn de vier hoeken bij P
genummerd. De hoeken van driehoek ABC geven we opvolgend aan met a, b, g. Nu geldt: P1 + P2 + P3 + b = 180° P2 + P3 + P4 + b = 180° 2 Verklaar deze uitdrukkingen. Wat kan je hieruit concluderen omtrent P1 en P4? 2 Aan welke hoek in CPB'A' is P4 gelijk? Waarom? Aan welke hoek in AB'PC' is P1 gelijk? Waarom? 2 Waarom zijn de punten A', B', C' nu collineair? |
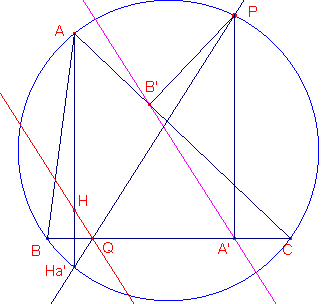
We bewijzen in deze paragraaf een (wellicht al bekende) eigenschap van het hoogtepunt van een driehoek in samenhang met de omcirkel.
Kies een nieuw werkblad. Teken een driehoek ABC met z'n omcirkel.
Teken ook de hoogtelijnen uit A en B. Geef het hoogtepunt aan met H.
De hoogtelijn uit A snijdt de zijde BC in een punt dat meestal wordt aangegeven met Ha. Het snijpunt van deze hoogtelijn met de omcirkel geven we aan met Ha'.
Meet de afstand tussen de punten H en Ha en de afstand tussen de punten Ha en Ha'.
2 Wat valt je op?
Bekijk deze eigenschap voor verschillende driehoeken.
Klik hier
voor een CabriJavapplet bij Opdracht 6a.
| figuur 5 |  |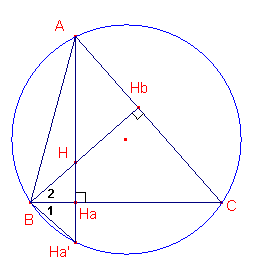
Voor het bewijs van de eigenschap uit
Opdracht 6a tekenen we het lijnstuk BHa'. 2 Waarom zijn de driehoeken HBHa en HAHb gelijkvormig? Wat weet je nu van ÐB2 en ÐHAHb? ÐHAHb en ÐB1 zijn beide omtrekshoeken. 2 Op welke boog van de omcirkel staan ze? Wat weet je nu van ÐHAHb en ÐB1? 2 Waarom zijn de driehoeken HBHa en Ha'BHa nu congruent? |
We kunnen hetgeen we zojuist gevonden hebben ook als volgt formuleren:
| Stelling 2 Het spiegelbeeld van het hoogtepunt in een zijde van de driehoek ligt op de omcirkel van die driehoek. |
We zullen deze eigenschap in de volgende paragraaf gebruiken.
Laad het bestand ‘startsimson.fig’ (zie eventueel Opdracht 1 en Opdracht 2).
| figuur 6a |  |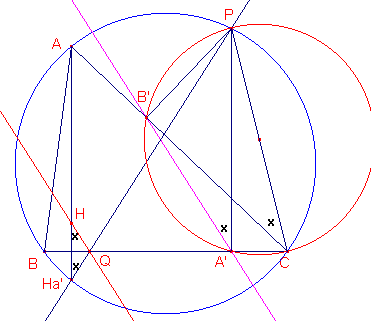
Teken in die figuur ook de hoogtelijn
uit A en het hoogtepunt H. De lijn PHa' snijdt de zijde BC van de driehoek in het punt Q. Teken ook de lijn HQ. Bekijk de positie van de lijn HQ ten opzichte van de lijn s(P), als P over de omcirkel beweegt. 2 Wat is je conclusie? Klik hier
Ook dit vraagt natuurlijk om een bewijs. |
| figuur 6b |  |
In figuur 6b zijn enkele gelijke
hoeken met een x aangegeven. 2 Geef aan waarom deze hoeken inderdaad aan elkaar gelijk zijn (maak daarbij gebruik van de Stelling 2). 2 Bewijs op basis hiervan dat de lijnen HQ en s(P) evenwijdig zijn. Een gevolg van deze laatste eigenschap is: |
| . |
| Stelling 3 De lijn s(P) deelt het lijnstuk PH middendoor. |
2 Bewijs nu zelf Stelling 3.
Aanwijzing
Toon eerst aan, dat de lijn A'B' zwaartelijn naar PQ is in de rechthoekige driehoek PA'Q.
Gebruik dan de eigenschap, dat HQ evenwijdig is met s(P) in driehoek PHQ.
| figuur 7 |  |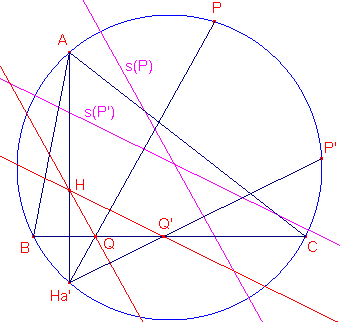
In de figuur hiernaast zijn de
s-lijnen van de punten P en P' getekend (P en P' zijn willekeurige punten van de
omcirkel). 2 Bewijs dat de hoek tussen s(P) en s(P') gelijk is aan ½bg(PP').
Klik hier Een gevolg hiervan staat in Stelling 4. |
| . |
Wanneer de punten P en P' eindpunten zijn van een middellijn van de omcirkel van een driehoek, dan staan de lijnen s(P) en s(P') loodrecht op elkaar. 2 Verklaar de juistheid van deze stelling! Klik hier
voor een CabriJavapplet die deze
stelling illustreert.
Het bewijs dat in Opdracht 9 werd gevraagd, kan ook op een iets andere manier worden gegeven.
Bekijk daartoe eerst figuur 8a.
figuur 8a  |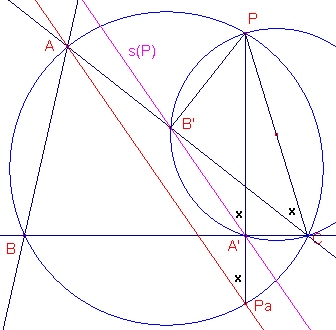
figuur 8b  |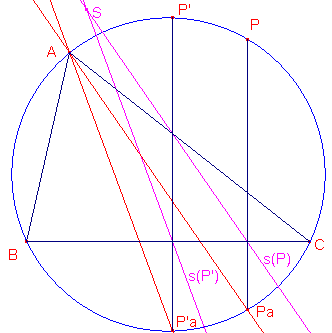
In figuur 8a is weer in enkele hoeken
een x geplaatst
om aan te geven dat die hoeken gelijk zijn. De loodlijn uit P op BC snijdt de omcirkel in het punt Pa. 2 Verklaar de juistheid van de in de hoeken geplaatste kruisjes. 2 Bewijs hiermee dat APa // s(P). |
In figuur 8b zijn de Simson-lijnen van twee willekeurige punten P en P' van de omcirkel getekend, evenals de punten P
a en P'a.2 Bewijs nu opnieuw, maar op een andere manier dan in Opdracht 9, dat Ð(s(P), s(P')) = ½ bg(PP').
Opmerking
Uit figuur 8a volgt een snelle manier om de Simson-lijn van een punt P te tekenen.
2 Beschrijf deze methode.
[einde Opmerking]
| figuur 9 |  |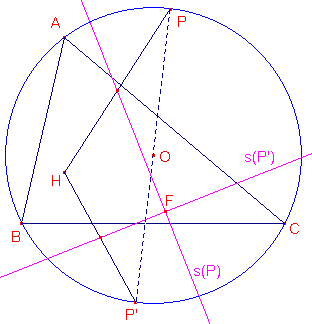
2 Ga na wat de meetkundige plaats is van het snijpunt F van twee
loodrecht op elkaar staande Simson-lijnen (zie Stelling 4). 2 Geef hiervoor (indien mogelijk) een korte verklaring. Klik hier voor een CabriJavapplet ter
illustratie. |
Klik hier voor een CabriJavapplet
hierbij.
Aanwijzing
Bekijk de situatie vanuit het punt P.
Kijk ook nog eens naar Stelling 3. Waar ligt het punt S?
Kan je nu ook bewijzen dat bij veranderlijke P op de omcirkel de Steiner-lijn steeds door
H gaat?
2 Geef
dan dat bewijs ook.
5. Download
De in de applets gebruikte Cabri-figuren zijn in een bestand te downloaden via deze
website.
In het bestand is ook een macro:SimsonLijn opgenomen.
Klik hier om het downloaden van dit bestand
te starten [8kB, ZIP formaat].
Dit werkblad is NIET MEER als PDF-bestand beschikbaar.
[simsonw.htm] laatste wijziging op:
19-01-18